Переходные процессы. ВАРИАНТ 3. Расчет трехфазной цепи переменного тока при соединении фаз приемника энергии звездой
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
РАСЧЕТ ТРЕХФАЗНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА ПРИ СОЕДИНЕНИИ ФАЗ ПРИЕМНИКА ЭНЕРГИИ ЗВЕЗДОЙ В схеме трехфазной цепи (рис. 1) заданы: линейное напряжение: 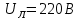 комплексные сопротивления фаз нагрузки: 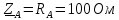 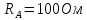 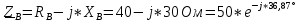 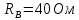 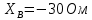 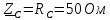 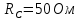  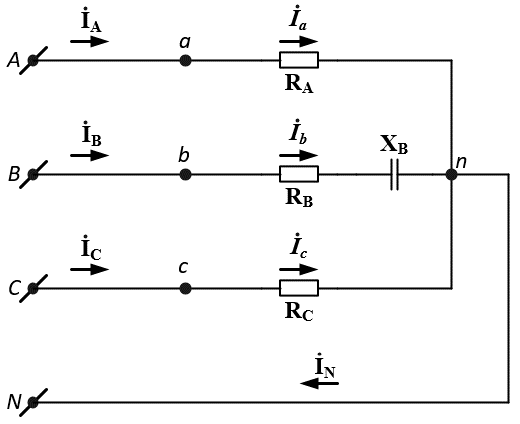 Рисунок 1 – Схема трехфазной цепи при соединении фаз приемника звездой с нулевым приводом Требуется: 1. Вычислить фазные токи 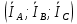 и ток в нейтральном проводе и ток в нейтральном проводе 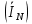 . .2. Найти активную 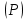 и реактивную и реактивную 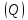 мощности цепи. мощности цепи.3. По данным расчета построить векторную диаграмму напряжений и токов. Решение: При несимметричной нагрузке, соединенной звездой и наличии нулевого провода, сопротивление которого 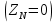 равно нулю, напряжение смещения нейтрали равно нулю: равно нулю, напряжение смещения нейтрали равно нулю: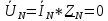 поэтому фазные напряжения приемника: 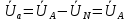 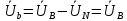 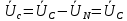 Фазное напряжение генератора: 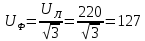 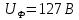 Система фазных напряжений генератора в комплексной форме. 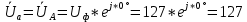 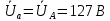 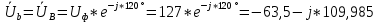 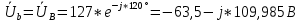 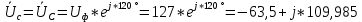 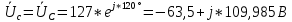 Система линейных напряжений генератора и приемника: 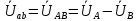 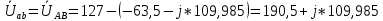 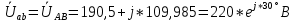 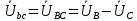 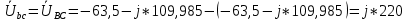 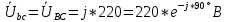 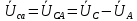 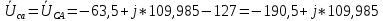 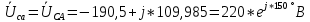 Фазные (линейные) токи приемника: 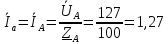 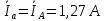 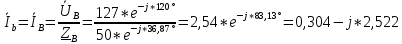 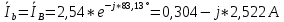 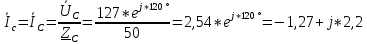 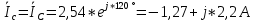 Ток в нулевом проводе: 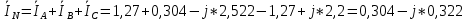 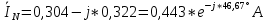 Напряжения на отдельных элементах цепи: 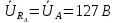 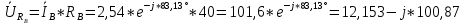 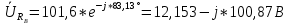 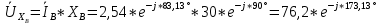 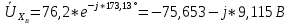 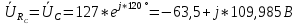 Определим полную, активную и реактивную мощности трехфазной цепи: комплекснаая полная мощность: 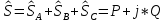 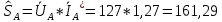 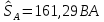 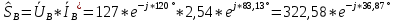 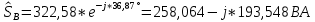 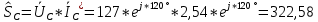 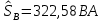 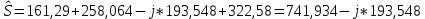 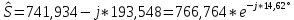 Активная мощность равна вещественной части комплексной полной мощности: 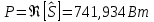 Реактивная мощность равна мнимой части комплексной полной мощности: 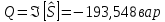 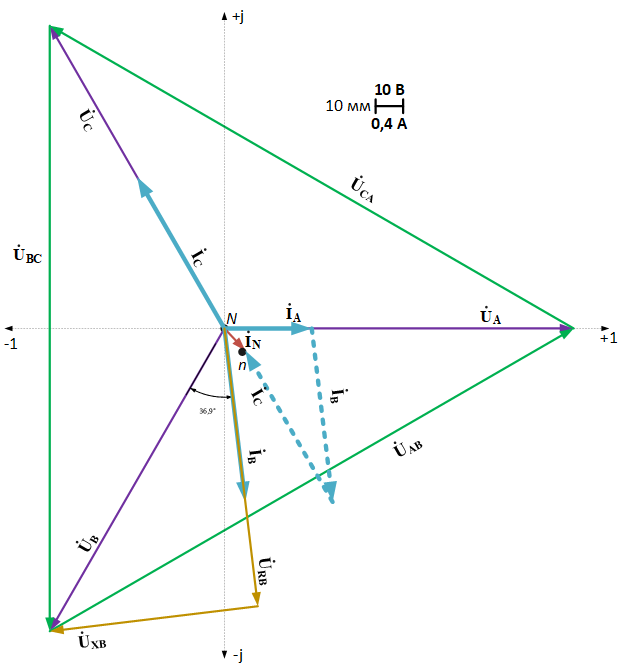 Рисунок 2 – Векторная диаграмма токов и напряжений Практическое расчетно-графическое задание 05 Расчёт методом симметричных составляющих цепи c несимметричным участком в линии Симметричная трехфазная цепь питается от трехфазного генератора с симметричной системой ЭДС, фазные обмотки которого соединены в звезду. В результате повреждения линии (короткого замыкания фаз «А» и «В» на землю), соединяющей генератор и нагрузку, в цепи возникает поперечный несимметричный участок (рис. 1). 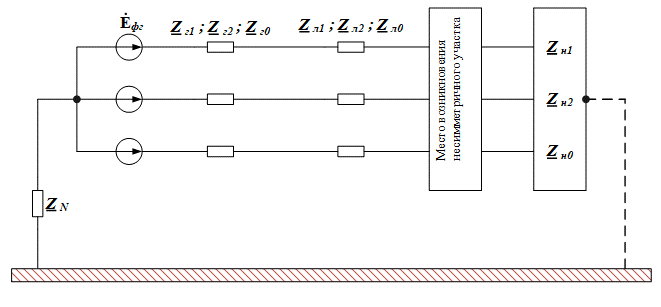 Рисунок 1 – Исходная схема цепи Параметры цепи: Вид повреждения линии – короткое замыкание (двухфазное) фаз «А» и «В» на землю. 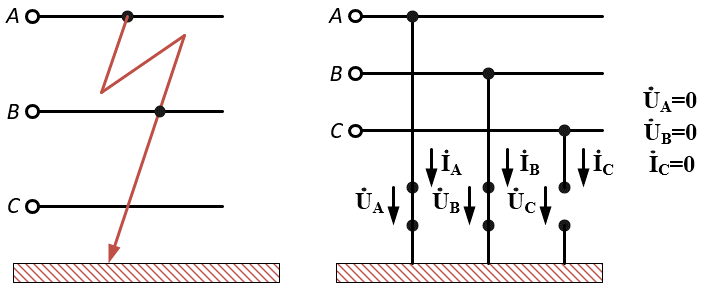 Рисунок 2 – Двухфазное короткое замыкание на землю Схема соединения нагрузки – звезда с нейтральным проводом. Фазная ЭДС генератора: 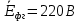 Сопротивление нейтрального провода: 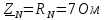 Фазные сопротивления прямой, обратной и нулевой последовательностей для генератора: 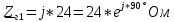 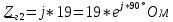 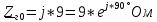 Фазные сопротивления прямой, обратной и нулевой последовательностей для линии: 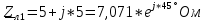 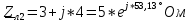 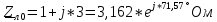 Фазные сопротивления прямой, обратной и нулевой последовательностей для нагрузки: 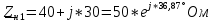 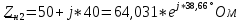 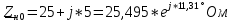 Требуется: Методом симметричных составляющих определить фазные токи 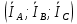 , и фазные напряжения , и фазные напряжения 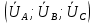 несимметричного участка и построить векторные диаграммы найденных фазных токов и напряжений и их симметричных составляющих. несимметричного участка и построить векторные диаграммы найденных фазных токов и напряжений и их симметричных составляющих.Решение: Несимметричный участок в линии заменим эквивалентным источником с несимметричной системой напряжений 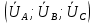 . .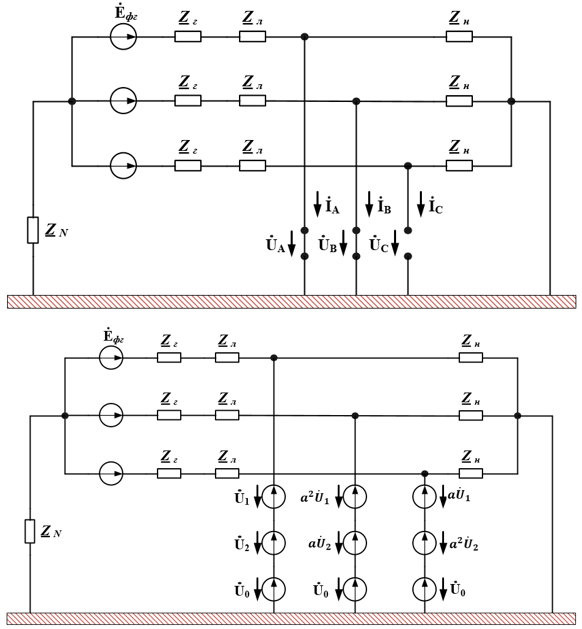 Рисунок 3 – Трехфазная цепь с коротким замыканием фаз «А» и «В» на землю Оператор фазы (или фазный множитель) – это такой вектор, скалярная величина которого равна 1 и который в комплексной плоскости образует с положительной осью вещественных количеств угол 120°. 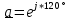 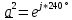 Используя оператор фазы, напряжения систем прямой и обратной последовательностей для фаз «В» и «С» можно выразить через напряжения фазы «А». 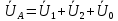 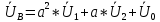 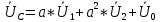 Системы трех несимметричных напряжений 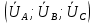 и трех несимметричных токов и трех несимметричных токов 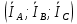 в месте несимметрии представим в виде суммы трех симметричных систем: прямой обратной и нулевой последовательности, симметричные составляющие которых в месте несимметрии представим в виде суммы трех симметричных систем: прямой обратной и нулевой последовательности, симметричные составляющие которых 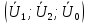 и и 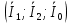 нужно определить. нужно определить.Составим три однофазные схемы замещения, которые и будем использовать для расчета. 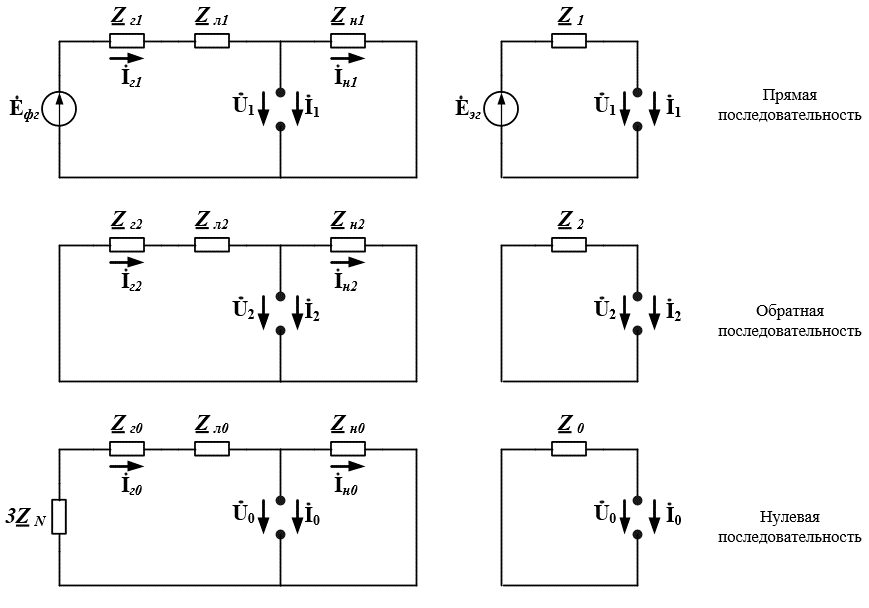 Рисунок 4 – Однофазные схемы замещения и преобразованные схемы замещения последовательностей В схему прямой последовательности включены фазная ЭДС генератора и сопротивления всех элементов цепи прямой последовательности. 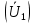 и и 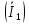 – симметричные составляющие напряжения и тока прямой последовательности в месте короткого замыкания. – симметричные составляющие напряжения и тока прямой последовательности в месте короткого замыкания.Конфигурация схемы обратной последовательности будет такая же, но схема не содержит ЭДС (так как действует симметричная система ЭДС на входе). В ней включены сопротивления всех элементов цепи обратной последовательности. 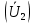 и и 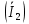 – симметричные составляющие напряжения и тока обратной последовательности в месте короткого замыкания. – симметричные составляющие напряжения и тока обратной последовательности в месте короткого замыкания.Конфигурация схемы нулевой последовательности отличается от схемы обратной последовательности только наличием утроенного сопротивления нейтрального провода. В ней включены сопротивления всех элементов цепи нулевой последовательности. 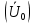 и и 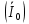 – симметричные составляющие напряжения и тока нулевой последовательности в месте короткого замыкания. – симметричные составляющие напряжения и тока нулевой последовательности в месте короткого замыкания.По методу симметричных составляющих вместо исходной схемы нужно рассчитать три трехфазные схемы: прямой, обратной и нулевой последовательностей. Но так как режимы в каждой из этих схем будут симметричны, расчет проводится только для одной фазы. Рассчитаем эквивалентную ЭДС в схеме прямой последовательности. Вычисления производим в программе «PTC Mathcad Prime 5.0». 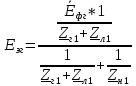 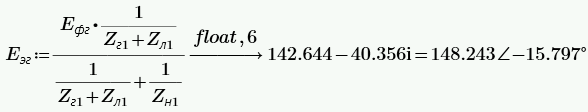 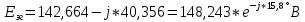 Эквивалентные сопротивления 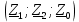 найдем по формулам эквивалентных преобразований для параллельных ветвей. найдем по формулам эквивалентных преобразований для параллельных ветвей.В схеме прямой последовательности: 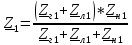  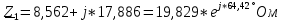 В схеме обратной последовательности: 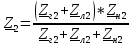 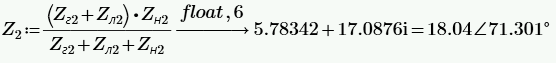 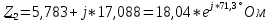 В схеме нулевой последовательности: 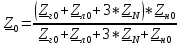 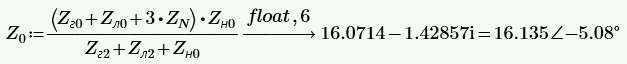 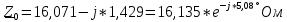 Для нахождения шести неизвестных симметричных составляющих 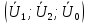 и и 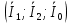 составим систему из шести уравнений: составим систему из шести уравнений:первые три уравнения запишем для схем замещения (рис. 4) по второму закону Кирхгофа; 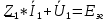 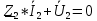 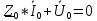 остальные три уравнения запишем по условиям короткого замыкания в месте несимметрии (короткое замыкание фаз «А» и «В» на землю). Граничные условия: 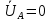 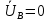 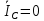 Составим систему шести уравнений: 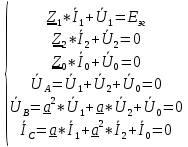 Систему уравнений решим в программе «PTC Mathcad Prime 5.0» с помощью встроенной функции «lsolve». Для решения составляется матрица коэффициентов и матрица свободных членов. Преобразуем систему к виду: 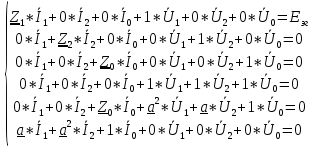 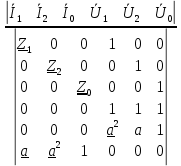 Матрица коэффициентов: 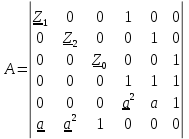 матрица свободных членов: 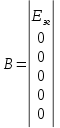  Решение системы: 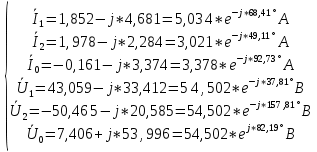 Симметричные составляющие токов в месте короткого замыкания: 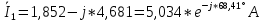 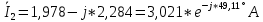 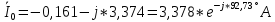 Симметричные составляющие напряжений в месте короткого замыкания: 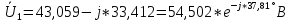 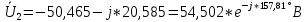 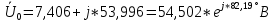 Зная симметричные составляющие, найдем токи и напряжения в месте короткого замыкания. Токи в месте короткого замыкания: 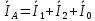 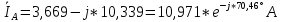 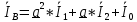 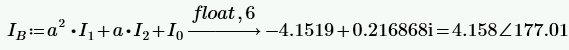 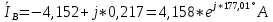 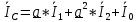 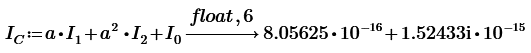 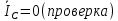 Напряжения в месте короткого замыкания: 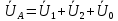 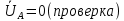 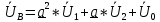 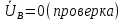 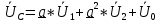 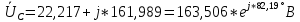 Для построения диаграмм тоже удобно пользоваться программой «Mathcad». Вектора можно построить, задавая их матрицами. Векторные диаграммы симметричных составляющих токов. Для прямой последовательности: 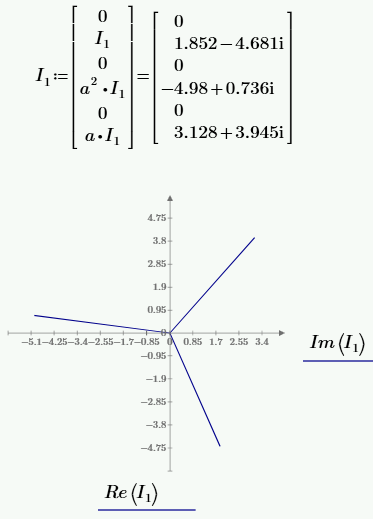 Для обратной последовательности: 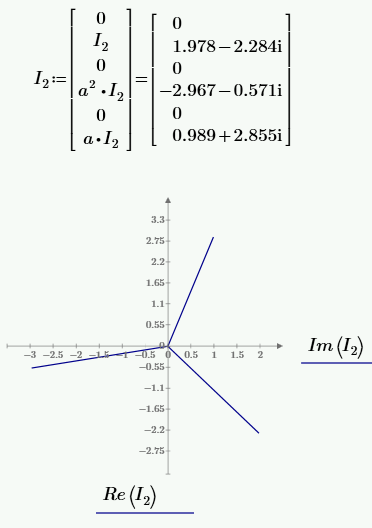 Для нулевой последовательности: 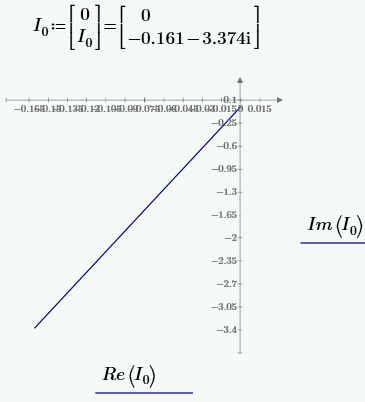 Векторные диаграммы симметричных составляющих напряжений. Для прямой последовательности: 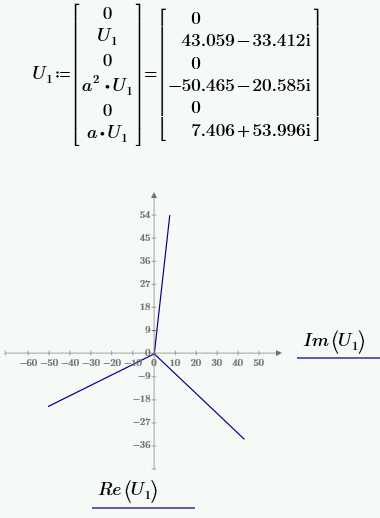 Для обратной последовательности: 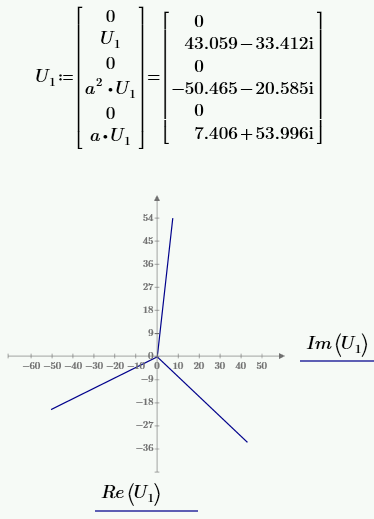 Для нулевой последовательности: 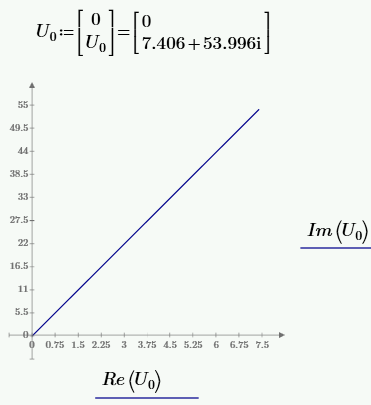 Векторная диаграмма токов в месте коротких замыканий 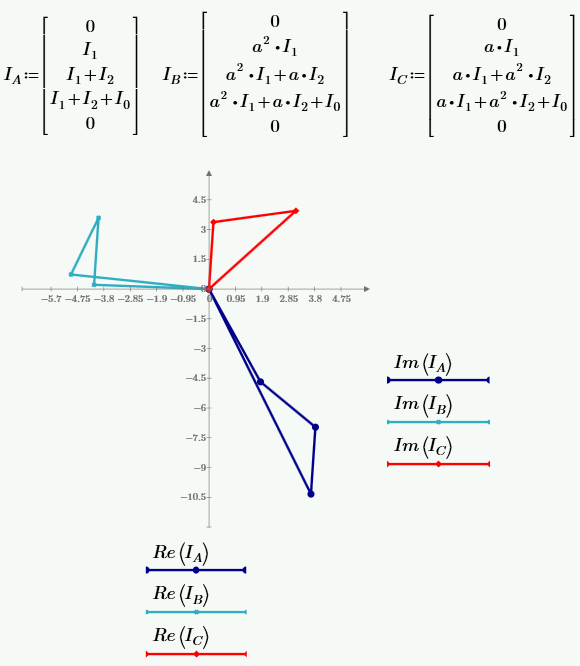 Векторная диаграмма напряжений в месте коротких замыканий 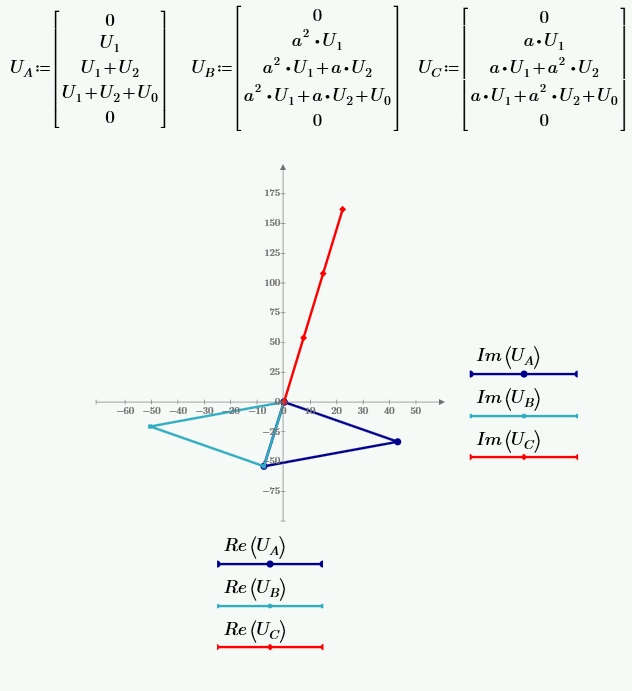 |
