ТОЭ. РГР№ 1. Расчетная графическая работа расчет линейной цепи постоянного тока

• Название: Расчетная графическая работа расчет линейной цепи постоянного тока
• Дата: 26.04.2023
• Размер: 218.5 Kb.
• Имя файла: РГР№ 1.doc
• Тип: Документы; #1090358

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ТЕОРЕТИЧЕСКИХ ОСНОВ ЭЛЕКТРОТЕХНИКИ

РАСЧЕТНАЯ ГРАФИЧЕСКАЯ РАБОТА

РАСЧЕТ ЛИНЕЙНОЙ ЦЕПИ ПОСТОЯННОГО ТОКА

Выполнил:

студент группы

УФА – 2011

Вариант №7.
Расчет линейной цепи постоянного тока.

1. 
   Определить все токи методом контурных токов.
   
2. 
   Определить все токи методом узловых напряжений, приняв потенциал 4–го узла =0.
   
3. 
   Произвести проверку по законам Кирхгофа.
   
4. 
   Составить баланс мощностей.
   
5. 
   Определить тока I₁ методом эквивалентного генератора.
   
6. 
   Начертить в масштабе потенциальную диаграмму для любого контура, включающего в себя 2 ЭДС.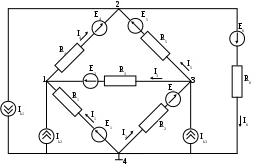
   

Исходные данные:


R₁ = 50 Ом E₁ = 0 В

R₂ = 20 Ом E₂ = 0 В J_k1 = 0 A

R₃ = 60 Ом E₃ = 400 В J_k2 = 0 A

R₄ = 90 Ом E₄ = 0 В J_k3 = -3 A

R₅ = 90 Ом E₅ = 0 В

R₆ = 10 Ом E₆ = -50 В
1. Расчет методом контурных токов.


E₃

1

2

R₄

I₄

I₂

R₆

I₆

I₅

I₁

I₃

R₅

R₃

R₂

R₁

3

4

I_k3

E₆




I₃₃


I₂₂


I₁₁




Рассчитаем собственные токи
I₁ = I₁₁ I₄ = I₂₂

I₂ = - I₁₁ + I₃₃ – J_k3 I₅ = -I₂₂ + I₃₃

I₃ = - I₁₁ + I₂₂ I₆ = I₃₃

Рассчитаем собственные сопротивления контуров и сопротивления смежных ветвей между контурами, взятые со знаком минус:
R₁₁ = R₁ + R₂ + R₃ = 50 + 20 + 60 = 130 Ом

R₂₂ = R₃ + R₄ + R₅ = 60 + 90 + 90 = 240 Ом

R₃₃ = R₂ + R₅ + R₆ = 20 + 90 + 10 = 120 Ом
R₁₂ = R₂₁ = - R₃ = -60 Ом

R₁₃ = R₃₁ = - R₂ = -20 Ом

R₂₃ = R₃₂ = - R₅ = -90 Ом
Рассчитаем сумму ЭДС, действующих в контуре:
E₁₁ = -E₃ - J_k3*R₂ = -400 + 60 = -340 B

E₂₂ = E₃ = 400 B

E₃₃ = J_k3*R₂ + E₆ = -60 - 50 = -110 B
Записываем систему уравнений :

Подставив значения сопротивлений и ЭДС получим следующую систему уравнений :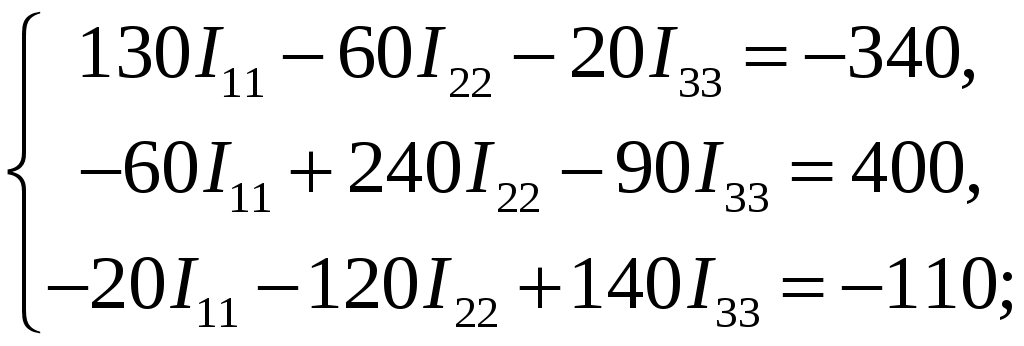

Решив систему, получим значения контурных токов :
I₁₁  - 2.34206 A

I₂₂  0,822291 A

I₃₃  - 0.69029 A

Находим токи в ветвях :
I₁ = - 2,34206 A I₄ = 0,822291 А

I₂ = 4.65177 А I₅ = -1,512581 А

I₃ = 3,164351 А I₆ = -0.69029 A


2. Расчет методом узловых потенциалов.

E₃

1

2

R₄

I₄

I₂

R₆

I₆

I₅

I₁

I₃

R₅

R₃

R₂

R₁

3

4

I_k3

E₆

I₁₁

I₂₂

I₃₃

φ₄=0


Записываем систему уравнений :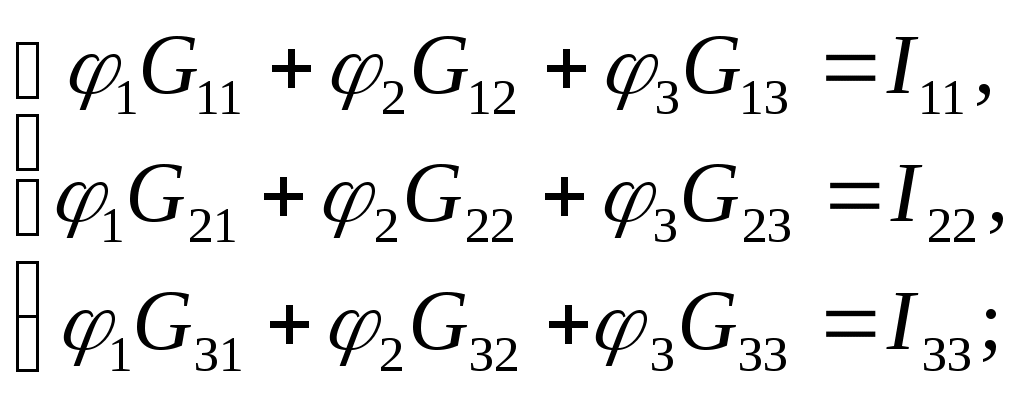


Подсчитываем проводимости, учитывая что в общем случае G_kk – сумма проводимостей ветвей, сходящихся в узле k; G_km– сумма проводимостей ветвей, непосредственно соединяющих узлы k и m , взятая со знаком минус :

См
См
С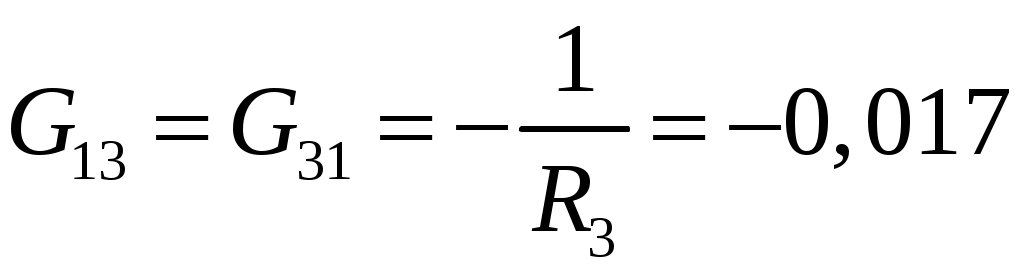м
См
См

См
При подсчете G₃₃ учтено, что проводимость ветви с источником тока равна нулю (сопротивление источника тока равно бесконечности).
Находим узловые токи, учитывая, что если к k – узлу подтекает ток от источника тока, то его надо брать со знаком “+”, если этот ток от источника тока утекает, то со знаком “-”:
А

А

А
Система уравнений :

Имеет решение :

₁ = 115,9772 В

₂ = 43,0934 В

₃ = -92,5777 В

Заключительный этап расчета состоит в подсчете токов по закону Ома :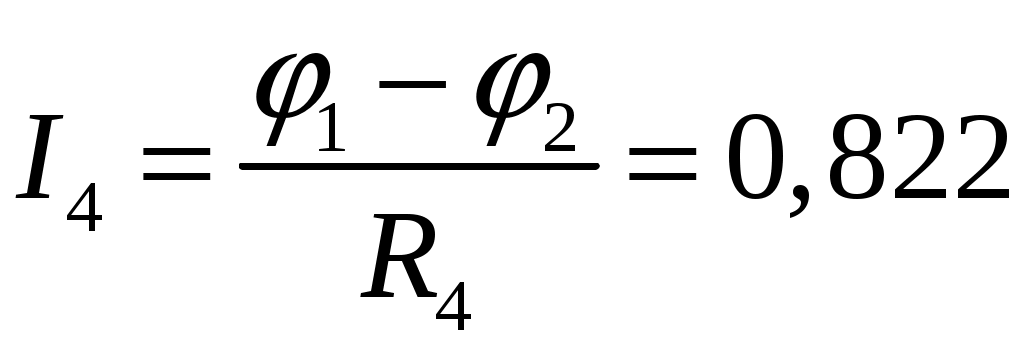
А

А

А

А

А

А

3. Проверка по законам Кирхгофа
Первый закон Кирхгофа :

“ Алгебраическая сумма токов в узле равна 0”
Составим уравнения для узлов :
1 : I₁ + I₃ – I₄ = 0

-2,34206+3,164351-0,822291 ≈ 0

2 : I₄ + I₅ – I₆ = 0

0,822291-1,512581+0,69029≈ 0

3 : I₂ – I₃ – I₅ + J_k3 = 0

4,65177-3,164351+1,512581-3≈ 0
Первый закон Кирхгофа для узлов 1, 2, 3 выполняется.
Второй закон Кирхгофа :

“Алгебраическая сумма падений напряжений в контуре равна алгебраической сумме ЭДС, действующей в этом контуре”
Составим уравнения для контуров :
123 : I₃R₃ + I₄R₄ – I₅R₅ = E₃

3,164351*60 + 0,822291*90 + 1,512581*90 = 399.97 ≈ E₃

134 : I₁R₁ – I₂R₂ – I₃R₃ = - E₃

- 117,103 – 93,0354-189,86106 = -399.99 ≈ - E₃

234 : I₂R₂ + I₅R₅ + I₆R₆ = E₆

93,0354 – 136,13229 – 6,9029 = -49,99998 ≈ E₆
Второй закон Кирхгофа для контуров 123, 134, 234 выполняется.

4. Балансмощностей

I₁²R₁ + I₂²R₂ + I₃²R₃ + I₄²R₄ + I₅²R₅ + I₆²R₆ = E₃I₃ + E₆I₆ + J_k3₃₃
274,26 + 432,779 + 600,787 + 60,855 + 205,911+ 4,765 = 1579,357
1265,7407 + 34,513 + 277,731 = 1578,985
1579,357 ≈ 1578,985
Баланс мощностей соблюдается.


5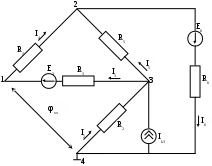
. Определение тока I₁ методом эквивалентного генератора

Разомкнем ветвь с резистором R₁ и найдем напряжение холостого хода между точками 4 и 1 :

Пусть ₄ = 0, тогда _xx = - ₁


Подставляем значения сопротивлений, ЭДС и источника тока :

Решая систему уравнений, получим :
₁ = 279,171 В

₂ = 54,638 В

₃ = -69,278 В

_xx = - ₁ = -279,171 В

Подсчитываем входное сопротивление R_вх всей схемы по отношению к зажимам 12 при закороченных источниках ЭДС и разомкнутых ветвях с источниками тока:





R₂


R₆
















R₈


R₇


R₉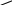










R₁₀


R₇









R_вх


R₁₁


Ом

Ом

Ом

Ом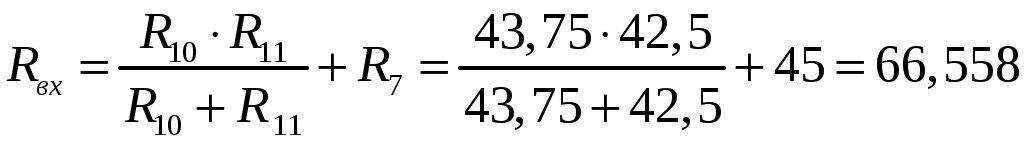

Ом

Ом
Определяем ток в ветви :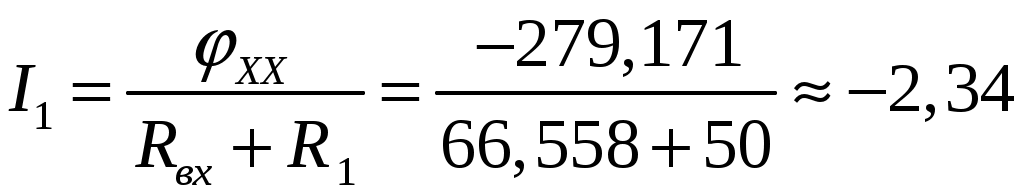
А
6. Потенциальная диаграмма
Построим потенциальную диаграмму для контура 4-3-1-2-4, содержащего в себе 2 ЭДС :




Подсчитаем суммарное сопротивление контура :
R_общ = R₂ + R₃ + R₄ + R₆ = 20 + 60 + 90 + 10 = 180 Ом
Произвольно примем потенциал одной из точек, например точки 4 , ₄=0. Эту точку на диаграмме поместим в начало координат.
Потенциалы точек :
3 : ₃ = ₄ - I₂R₂ = -93,035 В

3.1 : _3.1 = ₃ - I₃R₃ = -93,035 – 266.56 = -282,896 В

1 : ₁ = _3.1 + E₃ = 117,104 В

2 : ₂ = ₁ – I₄R₄ = 117,104 – 49.2 = 43,098 В

2.4 : _2.4 = ₂ – I₆R₆ = 43,098 + 6,903 = 50.00 В

4 : ₄ = _2.4 + E₃ = 0 В
При вычислении потенциала последующей точки через потенциал предыдущей IR брали со знаком “ - ”, если направление обхода совпадало с направлением тока, в обратном случае брали со знаком “ + ”.
График распределения потенциала вдоль замкнутого контура 4-3-1-2-4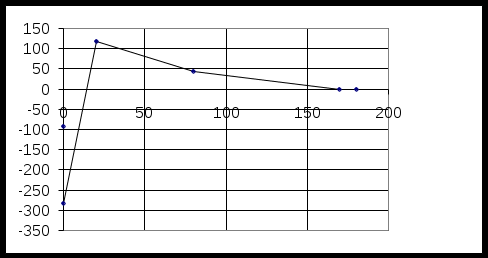