Контрольная по матем. РР№1. Расчетная работа
 Скачать 52.65 Kb. Скачать 52.65 Kb.
|
Расчетная работаВариант 53 1 2 3 1. Для определителя 4 1 4 ǀ 4 -1 4 ǀ М13 = ǀ 1 -1 1 ǀ = -3 ǀ 4 -1 5 ǀ Ответ: М13= -3 1 2 4 1 1 1 1 2 5 найти дополнительный минор элемента a13 . 1 2 5 1 1 1 2. Найти матрицы [АВ], [ВА], [А-1], если A 3 0 6 , B 2 3 3 . 4 3 4 Решение: ǀ 0 -15 -10 ǀ [А*В]= ǀ 3 -9 -3 ǀ ǀ 6 5 9 ǀ ǀ 6 5 5 ǀ [В*А]= ǀ 23 5 40 ǀ ǀ -9 -5 -11 ǀ ǀ -6 23/3 -4 ǀ [А-1]= ǀ 4 -16/3 3 ǀ ǀ 3 -11/3 2 ǀ 1 2 1 Проверить совместность системы уравнений и в случае совместности решить ее по правилу Крамера 2x1 x2 2x3 8 x1 x2 2x3 11 . 4x1 x2 4x3 22 Решение: Исследуем систему на совместность: 2 −1 2 ǀ 8 rank 1 1 2 ǀ 11 =3 4 1 4 ǀ 22 2 −1 2 rank 1 1 2 =3 4 1 4 Ранг расширенной матрицы равен рангу матрицы системы и равен числу неизвестных. Система совместна и имеет единственное решение. | 2 −1 2| Δ=| 1 1 2|=−6; | 4 1 4| | 8 −1 2| Δ1=| 11 1 2|=−6; | 22 1 4| | 2 8 2| Δ2=| 1 11 2|=−12; | 4 22 4| | 2 −1 8| Δ3=| 1 1 11|=−24 | 4 1 22| x1=Δ1/Δ=−6/−6=1 x2=Δ2/Δ=−12/−6=2 x3=Δ3/Δ=−24/−6=4 Ответ: x1=1 x2=2 x3=4 Доказать, что векторы a, b, c,образуют базис, и найти координаты вектора dв этом a базисе: 2,1,3, b 3,, c 5,3,1, d 31,6,22. Решение: Вычислим определитель матрицы: ǀ -2 1 3ǀ E =ǀ 3 -6 2ǀ ǀ-5 -3 -1ǀ ∆ = -2*((-6)*(-1) - (-3)*2) - 3*(1*(-1) - (-3)*3) + -5*(1*2 - (-6)*3) = -148 Определитель матрицы равен ∆ =-148 Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор d можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство: d = α1a + α2b + α3c Запишем данное равенство в координатной форме: (31;-6;22) = α(-2;1;3) + α(3;-6;2) + α(-5;-3;-1) Используя свойства векторов, получим следующее равенство: (31;-6;22) = (-2α1;1α1;3α1;) + (3α2;-6α2;2α2;) + (-5α3;-3α3;-1α3;) (31;-6;22) = (-2α1 + 3α2 -5α3;1α1 -6α2 -3α3;3α1 + 2α2 -1α3) По свойству равенства векторов имеем: -2α1 + 3α2 -5α3 = 31 1α1 -6α2 -3α3 = -6 3α1 + 2α2 -1α3 = 22 Решаем полученную систему уравнений методом Крамера. Ответ: 3 d= 4 -5 d= 3a + 4b -5c Вершины пирамиды находятся в точках А(5,2,4), В(−3,5,−7), С(1,−5,8), D(9,−3,5). Найти объем пирамиды и длину высоты, опущенной из вершины С. Решение: Найдем вектор по координатам точек: AB=(Bx - Ax; By - Ay; Bz - Az) = (-3 - 5; 5 - 2; -7 – 4) = (-8; 3; -11) AC=(Cx - Ax; Cy - Ay; Cz - Az) = (1 - 5; -5 - 2; 8 – 4) = (-4; -7; 4) AD=(Dx - Ax; Dy - Ay; Dz - Az) = (9 - 5; -3 - 2; 5 – 4) = (4; -5; 1) V = 1/6(AB*(AC*AD)) Найдем смешанное произведение векторов: ǀ ABx ABy ABz ǀ ǀ -8 3 -11 ǀ AB*(AC*AD)= ǀ ACx ACy ACz ǀ = ǀ -4 -7 4 ǀ = ǀ ADx ADy ADz ǀ ǀ 4 -5 1 ǀ =(-8)*(-7)*1 + 3*4*4 + (-11)*(-4)*(-5) - (-11)*(-7)*4 – 3*(-4)*1 - (-8)*4*(-5) = 56 + 48 - 220 - 308 + 12 - 160 = -572 Найдем объем пирамиды: V=1/6*572=286/3=95.33 С другой стороны, объём пирамиды равен: V=1/3*S*h, где h - высота, опущенная из вершины C на грань ABD, S - площадь грани ABD. S=1/2ǀABǀ*ǀADǀ*siny=1/2ǀǀAB,ADǀǀ Векторное произведение равно: ǀ i j k ǀ ǀAB,ADǀ= ǀ-8 3 -11 ǀ=-52i -36j +28k ǀ 4 -5 1 ǀ Поэтому площадь грани: S=1/2*(522+362+282)0,5=34.58 Следовательно, высота пирамиды равна: h=3*V/S=(3*286/3)/34.58=8.27 Ответ:VABCD=95.33 ; h=8.27 Найти расстояние от точки M0до плоскости, проходящей через точки M1,M2,M3, если M1 2, 1, 1, M2 0, 3, 2, M3 3, 1, 4, M0 21, 20, 16. Решение: Уравнение плоскости, проходящей через точкиM1M2M3, имеет вид: ǀx-(-2) y-(-1) z-(-1) ǀ ǀ 2 4 3 ǀ=0 ǀ 5 2 -3 ǀ и раскрывая определитель, получим: -18x+21y-16z-31=0 Отклонение точки M0(x0,y0,z0) от плоскости Ax+By+Cz+D=0 равно: δ=Ax0+By0+Cz0+D/±(A2+B2+C2)½ δ= (-18*-21)+(21*20)+(-16*-16)-31/(182+212+162)½=378+420+256/(324+441+256)½=1054/31.95=32.989 Ответ: Расстояние от точкиM0 до плоскости равно | δ|=32.989 Написать канонические уравнения прямой 6x 5 y 4z 8 0, 6x 5 y 3z 4 0. Решение: Прямая задана в виде пересечения двух плоскостей. Нормальные вектора плоскостей: N1=(6,-5,-4), N2(6,5,3) Прямая лежит в обеих плоскостях, следовательно перпендикулярна векторам N1, N2 То есть, вектор a=[N1,N2] является направляющим вектором прямой. | I j k | a=[N1,N2]=| 6 -5 -4 |=5i-42j+60k | 6 5 3 | Полагая x=0 получим: -5y-4z+8=0 + 5y+3z+4=0 ↔ -z+12=0 ↔ z=12 5y+36+4=0 ↔ y=-8 Таким образом, прямая направлена вдоль вектора a(5,-42,60) и проходит через точку P0(0,-8,12) Её канонические уравнения принимают вид: x-0/5=y+8/-42=z-12/60 Ответ: x/5=y+8/-42=z-12/60 Найти точку пересечения прямой, заданной каноническими уравнениями, и плоскости x 3 y 4 z 4 , 7x y 4z 47 0. 1 5 2 Решение: Представим уравнение (1) в виде двух уравнений: x-3/-1=y-4/5 , x-3/-1=z-4/2 Сделаем перекрестное умножение: 5(x-3)=-1(y-4) ↔ 5x+y=19 2(x-3)=-1(z-4) ↔ 2x+z=10 Построим матричное уравнение для системы линейных уравнений: | 5 1 0 | |x| |19| | 2 0 1 | |y|=|10| | 7 0 4 | |z| |47| Решим систему линейных уравнений отностительно x, y, z: |x| |-7 | |y|= |54| |z| |24| Ответ: координаты точки пересечения прямой (-7,54,24) 2x2 6x 4 Вычислить предел lim x2 = 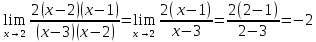 x2 5x 6 x3 4x2 28x x Вычислить предел lim 5x3 3x2 x 1 = 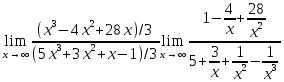 Сделаем замену:u= 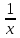 тогда 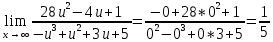 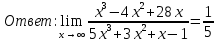   Вычислить предел lim32xx4 Вычислить предел lim32xx4x1 3x2 4x 1 .Домножим на 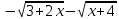 получим: 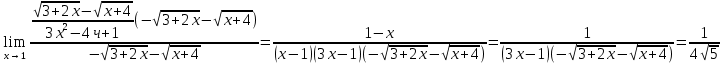 Ответ: 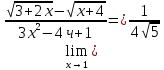 Вычислить предел limarctg6x x0 2x2 3x 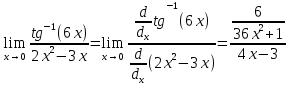 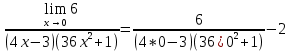 Ответ: 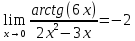 2x 5 5 x Вычислить предел lim 2x 1 x 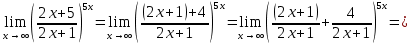 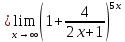 Сделаем замену: 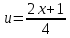 тогда: 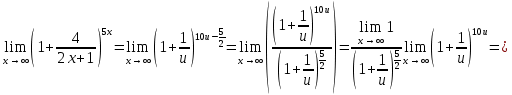 = 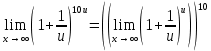 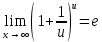 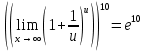 Ответ: 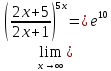 Составить уравнение нормали к данной кривой в точке с абсциссой x0 x3 , x0 1. Решение: f(x) в точке x0=1 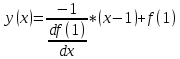 , f(1)=2 , f(1)=2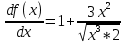 , , 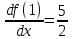 Таким образом, уравнение нормали имеет вид: 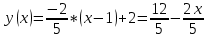 Ответ: 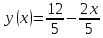 Найти дифференциал функции в точке с абсциссой x0 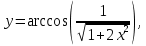 x=0 x=0Решение: Дифференциал функции y = f(x) в точке x0 вычисляется по формуле: dy=f´(x0)dx 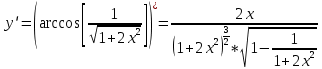 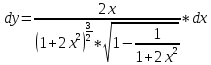 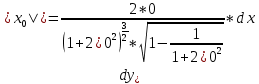 dy=f´(x0)dx mmmmmmmmmmmmmmmmmmmmm |
