Шабанов__Златоуст_2к_4сем_Теоретическая механика_КР-2. Расчетнографическая работа 2
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
Омский государственный университет путей сообщения (ОмГУПС) Кафедра «Теоретическая механика» Расчетно-графическая работа №2 Студент Р.  Г.Шабанов Г.ШабановСпец.190300 Уч. шифр 10891 30.03.2013 Руководитель – Омск 2013  Расчетно-графическая работа №2 Расчетно-графическая работа №2Вариант – 01 Динамика Задача № 1 Железнодорожный вагон М массой m, получив в точке A начальную скорость VA, движется по рельсам, которые на различных участках либо горизонтальны, либо наклонны под углом к горизонту (рис.1). Длина участка Рассматривая вагон в виде материальной точки, определить закон изменения скорости и закон движения вагона на участке AB, а также закон изменения скорости на участке BC. Единицу измерения коэффициента сопротивления следует определить самостоятельно из формулы силы сопротивления R. Исходные данные:
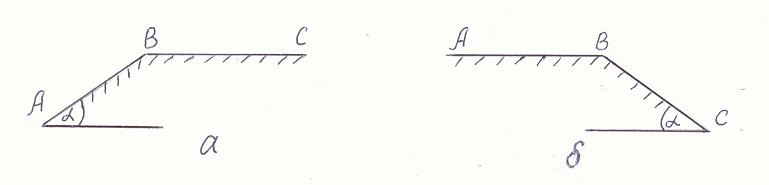 Рис.1(а) – Схема движения железнодорожного вагона.  Решение Решение1) Рассмотрим движение вагона на первом участке АВ Изображаем его на рисунке 1 (в виде материальной точки) в текущем (промежуточном положении). Указываем все действующие на вагон силы. Строим декартову систему координат Аху, взяв начало в начальном положении вагона и проведя ось Ах по АВ. 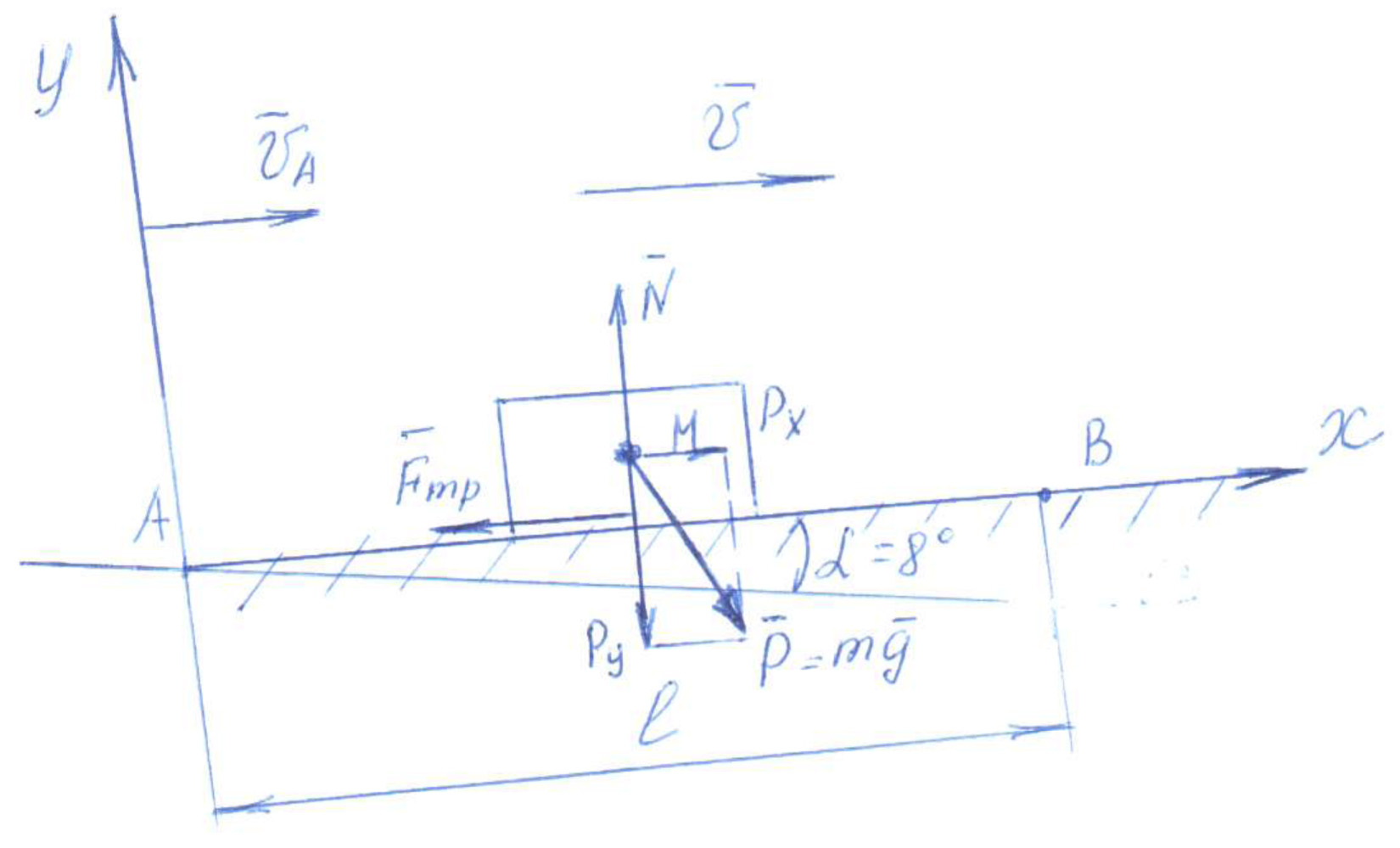 Рисунок 1 Действующие на вагон силы: Составляем дифференциальное уравнение движения вагона. Дифференциальное уравнение движения вагона в проекциях на оси декартовых координат Ах и Ау:  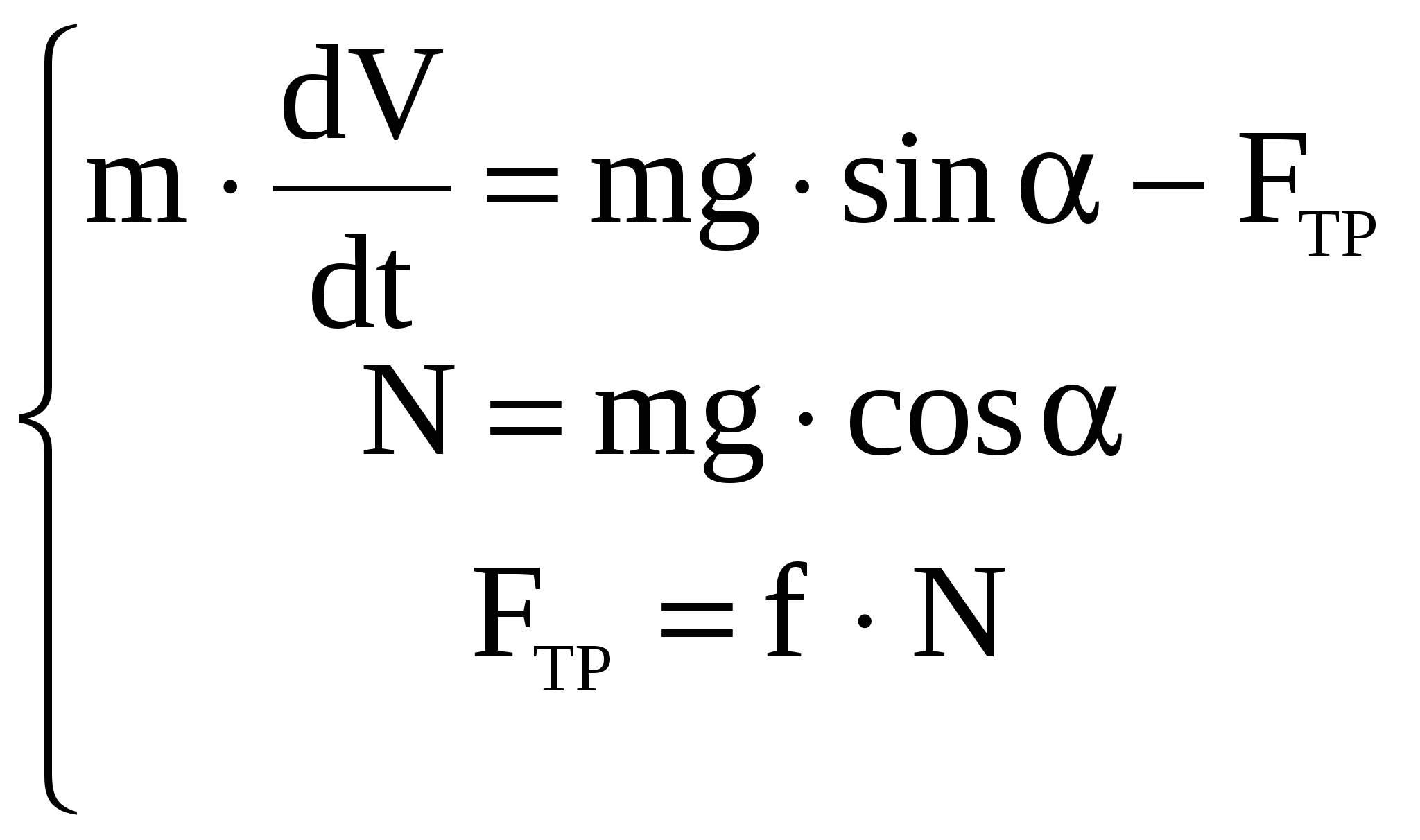 Получаем дифференциальное уравнение движения вагона на участке АВ: Решаем дифференциальное уравнение (3), подставив значения постоянных величин. V= + 0,888t+C Определяем постоянную интегрирования С . При Закон изменения скорости вагона на участке АВ в общей форме будет иметь вид: Определяем закон движения вагона на участке АВ Решаем дифференциальное уравнение (4). Определяем постоянную интегрирования С2 .  При При Получаем закон движения вагона на участке АВ в общей форме: Подставляя числовые значения в выражение (3), получаем: Закон изменения скорости вагона на участке АВ будет иметь вид: Подставляя числовые значения в выражение (5), получаем: Закон движения вагона на участке АВ: При Скорость вагона в точке В будет равна 2) Рассмотрим движение вагона на втором участке ВС Изображаем его на рисунке 2 (в виде материальной точки) в текущем (промежуточном положении). Указываем все действующие на вагон силы. Строим декартову систему координат Вху, взяв начало в начальном положении вагона и проведя ось Вх по ВС. 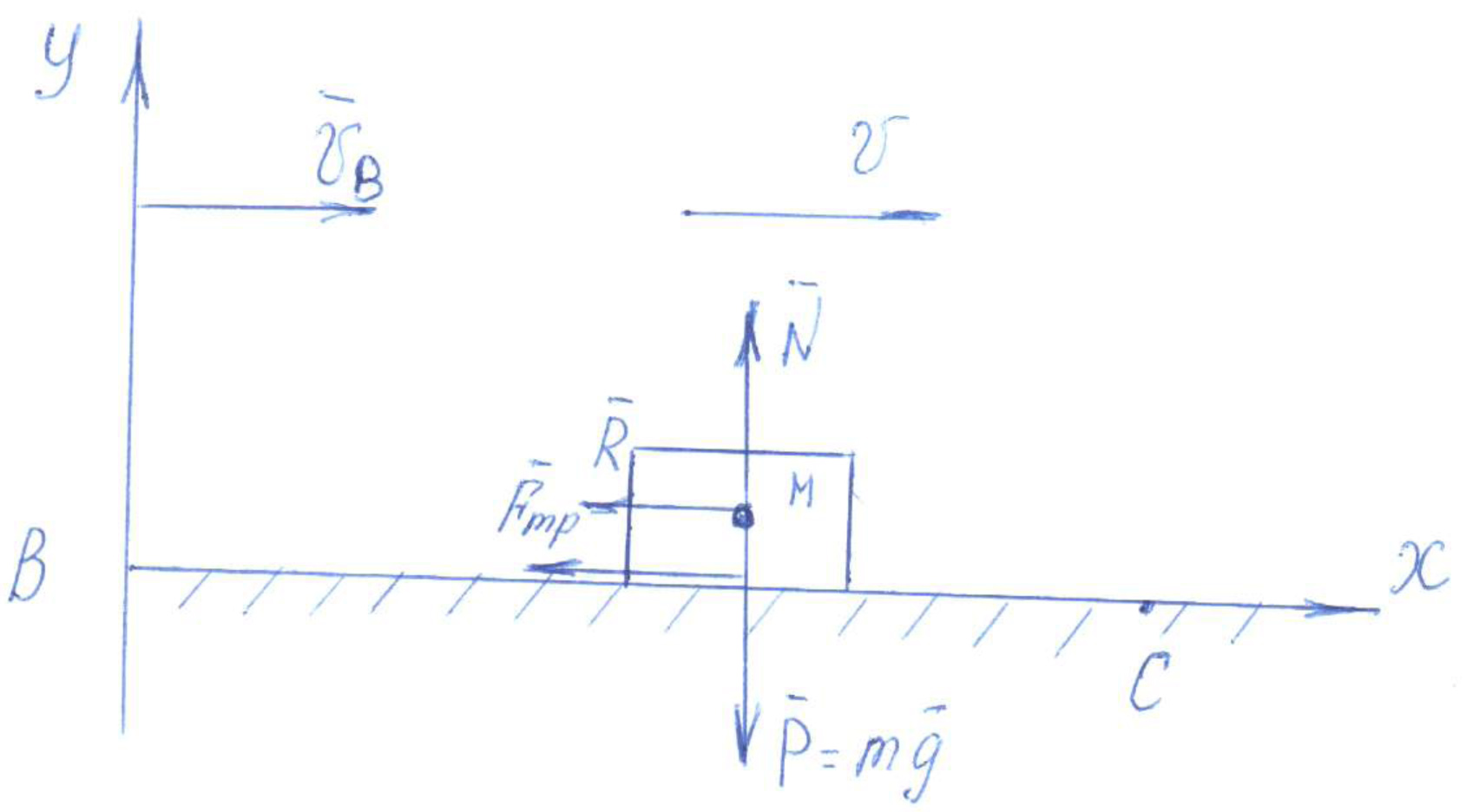 Рисунок 2. Действующие на вагон силы: Определяем единицу измерения коэффициента сопротивления : 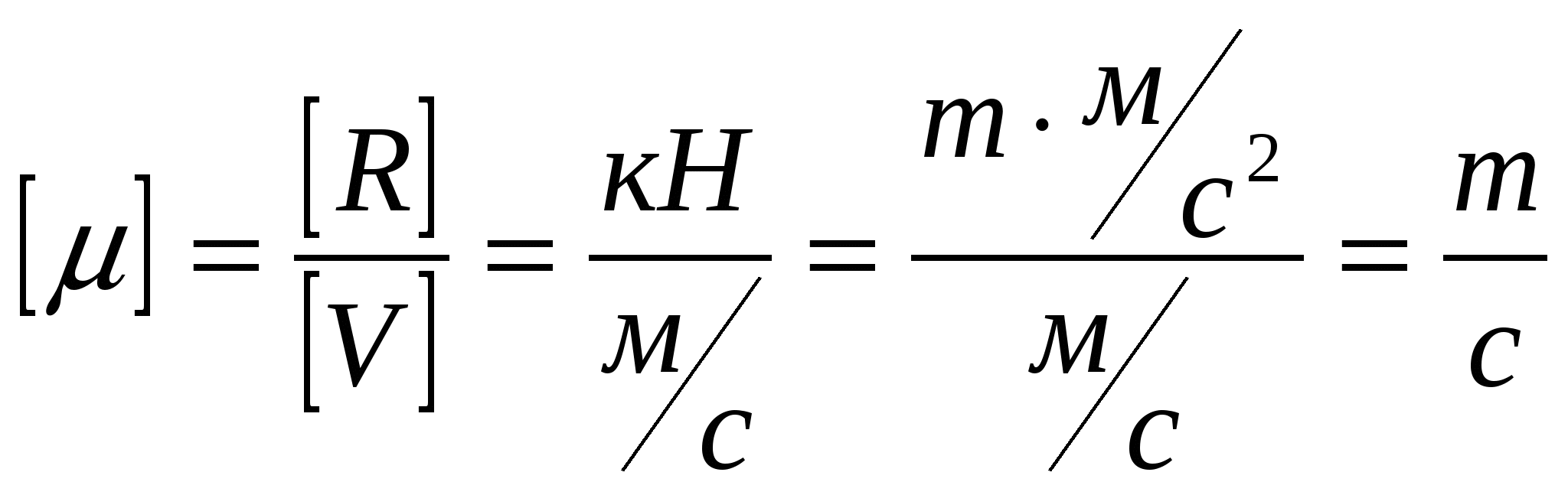 Составляем дифференциальное уравнение движения вагона.   Дифференциальное уравнение движения вагона в проекциях на оси декартовых координат Вх и Ву : 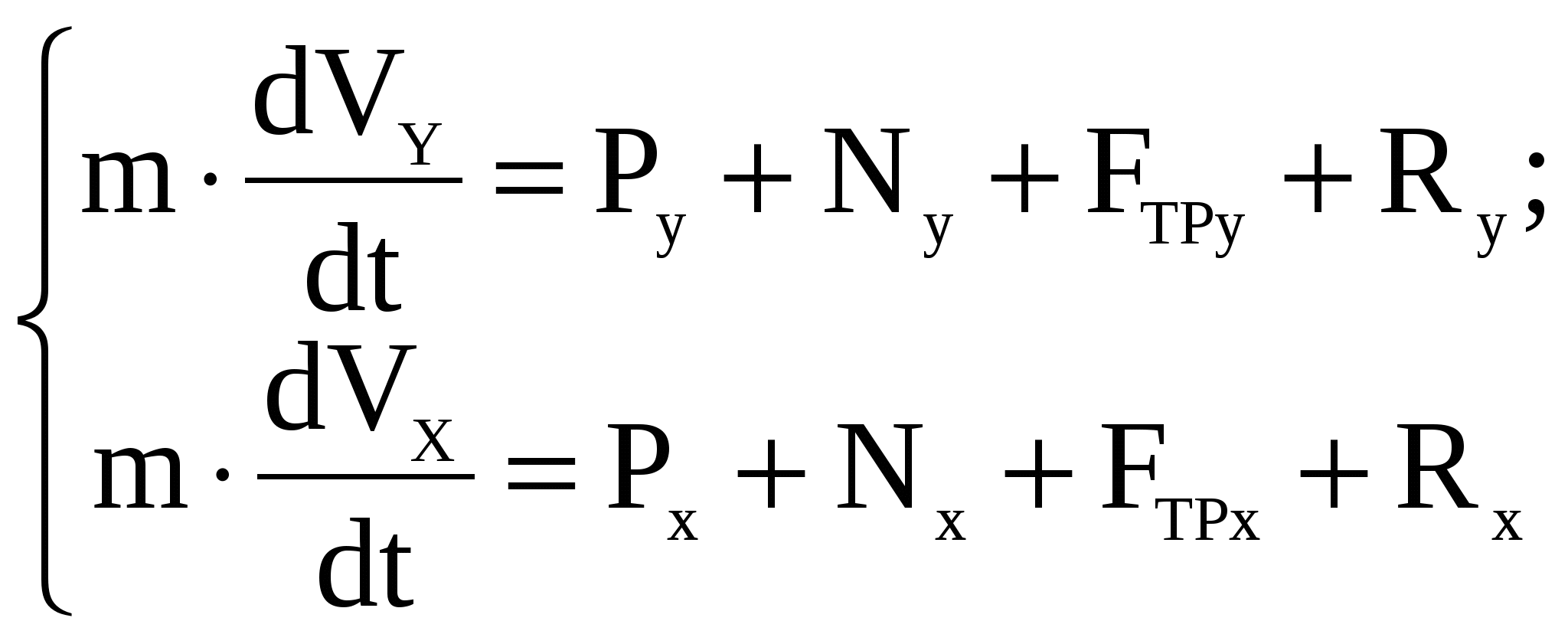 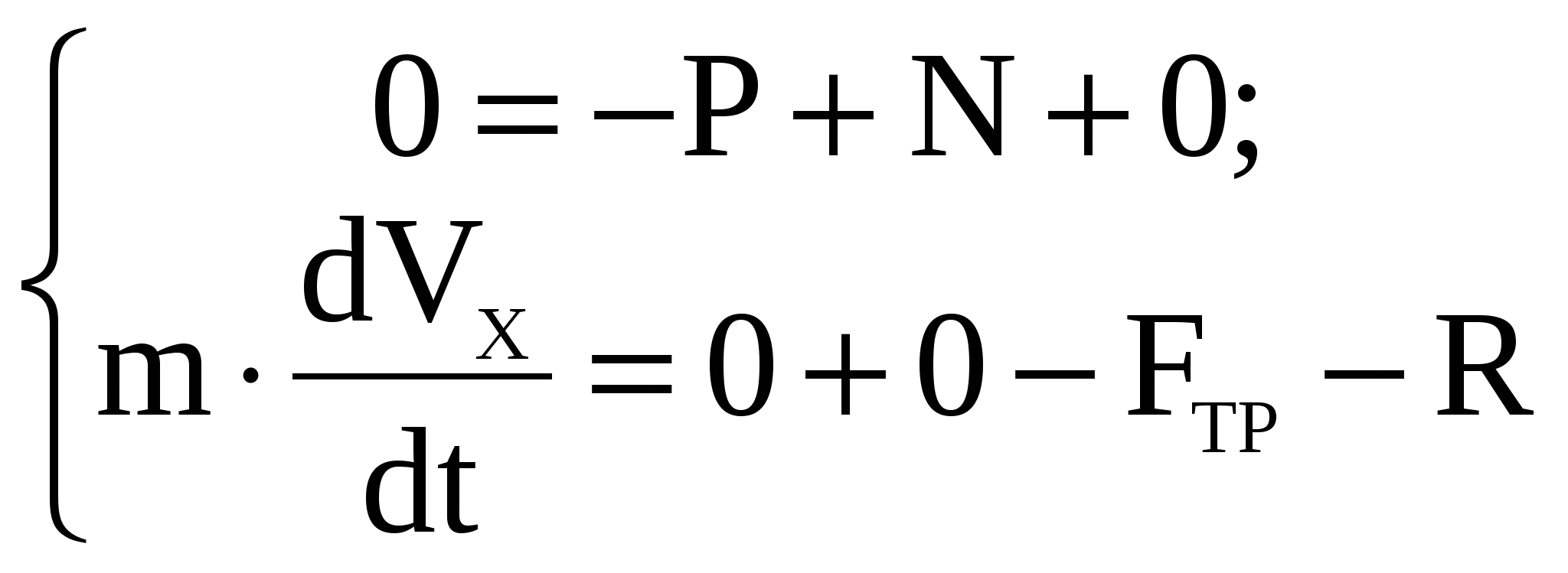 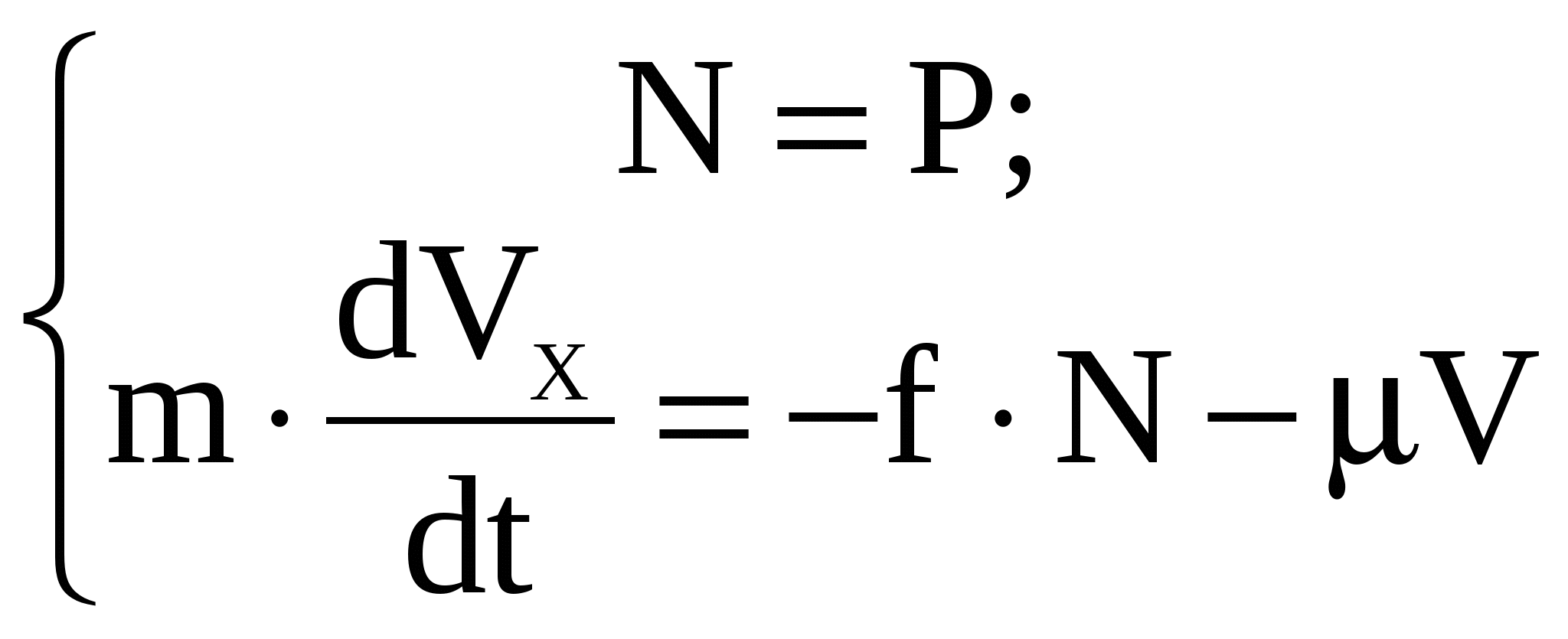 ; ; 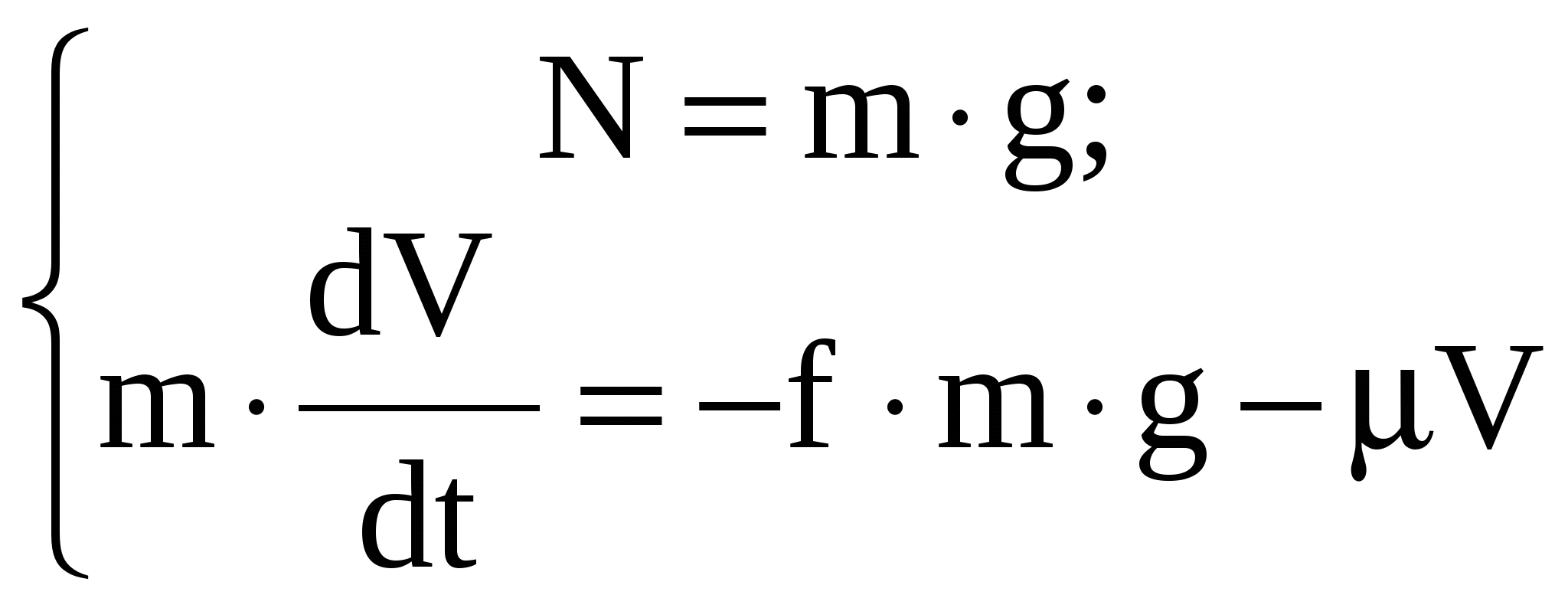 Получаем дифференциальное уравнение движения вагона на участке ВC: Решаем дифференциальное уравнение (2). 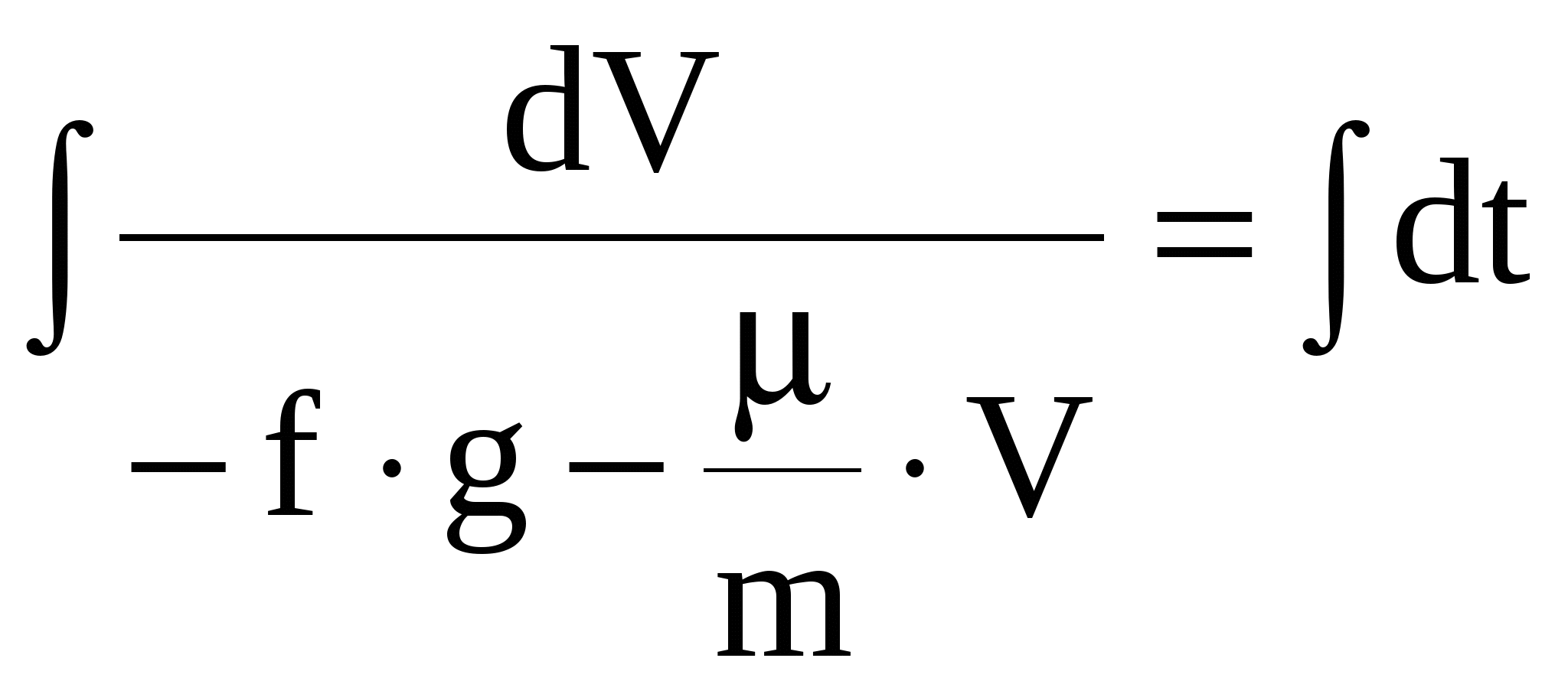 Для упрощения дальнейших расчетов подставляем в (3) числовые значения: Определяем постоянную интегрирования С. При При новом отсчете времени от начального момента в точке В, закон изменения скорости на участке BC будет иметь вид:   Задача № 2 Задача № 2Машинист электровоза посредством контроллера увеличивает мощность тяговых двигателей так, что модуль силы тяги Принимая электровоз за материальную точку, определить момент времени, когда он тронется с места, а также закон изменения скорости и уравнение движения. Участок пути считать горизонтальным. Исходные данные:
Решение 1) Изображаем электровоз на рисунке 3 (в виде материальной точки) в произвольный момент времени. Указываем все действующие на него силы. Сила   Рисунок 3. 2) Определите момент времени Электровоз трогается с места в момент времени, когда сила тяги превысит силы сопротивления движению, т.е: Подставляем (2), (3), (4) в (1), заменив для начального момента знак > на равенство. Подставляем в уравнение (5) числовые значения и определяем время начала движения Принимаем 3) Строим систему координат, взяв начало 0 в начальном положении электровоза и направив ось 0х по горизонтальному участку пути. Составляем дифференциальное уравнение движения электровоза в проекции на ось 0х. Проинтегрировав дважды дифференциальное уравнение, найдем закон изменения скорости и закон движения электровоза.  , (6) , (6) , (7) , (7) При При Закон изменения скорости электровоза: Определяем уравнение движения электровоза. Определяем постоянную интегрирования С2. При С2 = -0,031469 Закон изменения скорости электровоза: Уравнение движения электровоза:     Задача 3 Задача 3Механическая система состоит из груза массой , блока массой (большой радиус , меньший ), цилиндра массой и радиуса и призмы массой , находящейся на горизонтальной плоскости. Трение между призмой и плоскостью отсутствует. Груз получает перемещение =1 м относительно призмы вдоль ее поверхности влево или (в тех вариантах, где он висит) по вертикали вниз. Куда и на какое расстояние переместиться призма?
1) Построим неподвижную декартовую систему координат , взяв начало по левому краю призмы . 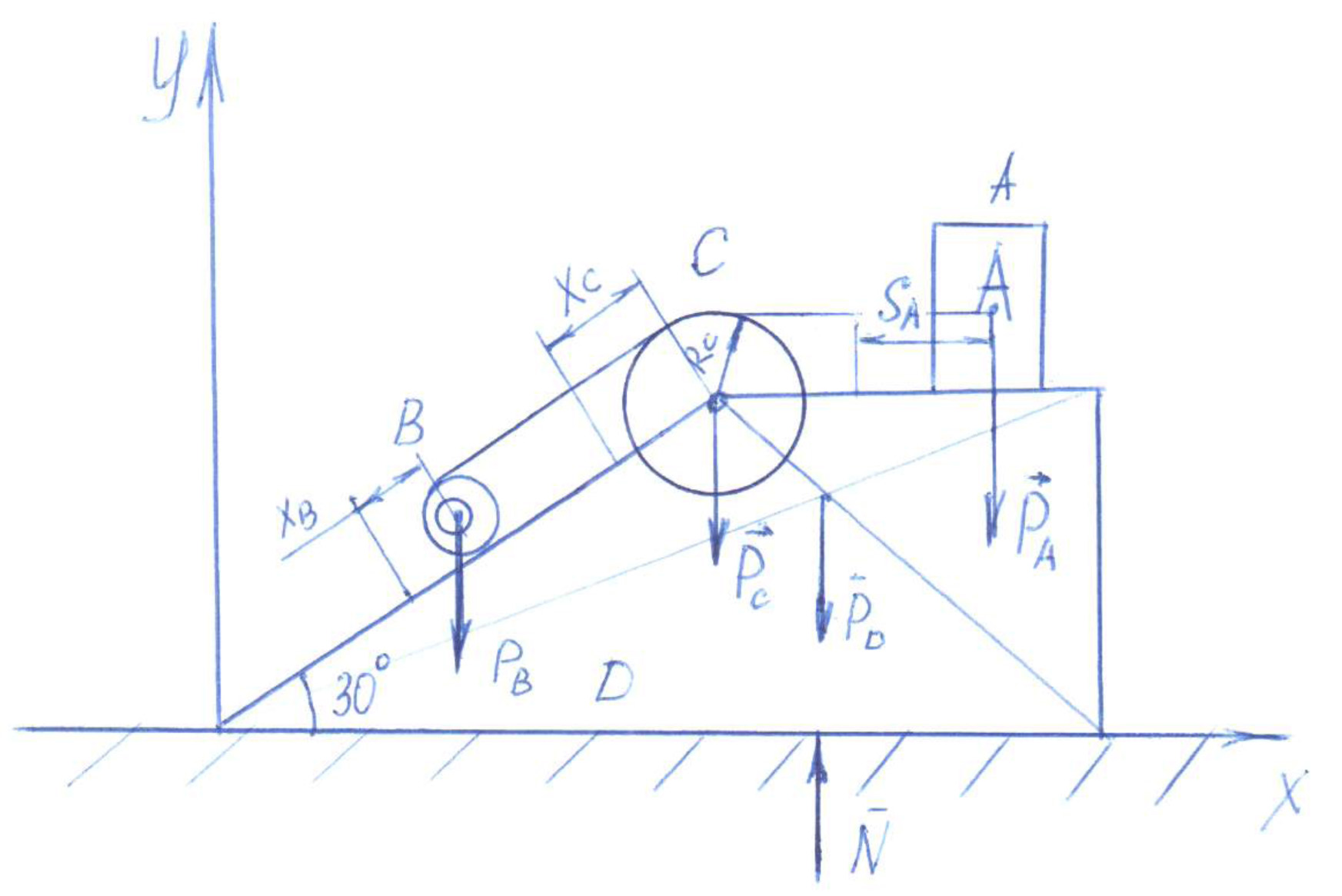 Рис. 1 – положение системы Предполагаем, что призма сместится направо. 2) Укажем на рисунке (рис. 1) все внешние активные (задаваемые) силы и реакции внешних связей, действующие на данную механическую систему. К ним относятся силы тяжести всех четырех тел – , , , , а также реакция опорной горизонтальной поверхности – . Силы тяжести всех тел приложены в их центрах тяжести (центр тяжести четырехугольной призмы находится в точке пересечения ее диагоналей), а положение точки приложения реакции связи не имеет принципиального значения. Все указанные силы направлены вдоль координатной оси . 3) Составим дифференциальное уравнение движения центра масс данной системы в проекции на горизонтальную ось : , (1) где: М – масса всей системы; – проекция ускорения центра масс всей системы на ось .  4) Проинтегрируем дважды дифференциальное уравнение (1), учитывая, что в начальный момент времени система находилась в покое. 4) Проинтегрируем дважды дифференциальное уравнение (1), учитывая, что в начальный момент времени система находилась в покое.В результате двойного интегрирования получим: Равенство (2) означает, что положение центра масс системы на координатной оси остается неизменным (несмотря на то, что отдельные тела в системе переместились по сравнению с их первоначальным положением). Отсюда следует, что координата центра масс системы вначале (когда все тела находились в покое) будет равна координате системы в конце (после перемещения отдельных тел в системе), т. е. будет выполняться равенство: . (3)  5). Воспользуемся формулами для определения координат центра масс системы вначале (когда она находилась в покое) и в конце (когда груз совершит перемещение ): 5). Воспользуемся формулами для определения координат центра масс системы вначале (когда она находилась в покое) и в конце (когда груз совершит перемещение ):где: , , , – массы тел , , и соответственно; , , , – начальные координаты центров масс тел , , , ; , , , – конечные координаты центров масс тел , , , . 6). После перемещения груза влево на расстояние призма переместится вправо на расстояние . Вследствие этого определятся абсолютные перемещения и остальных тел. Абсолютное перемещение тел А, В, С представляем как сумму относительного смещения, зависящего от величины SA относительного смещения груза А и неизвестного смещения ∆xD, равному абсолютному смещению призмы, относительно которой задавалось смещение SA. Перемещение центра цилиндра С относительно призмы и перемещение груза А связаны также, как связаны их скорости. Цилиндр С совершает плоское движение, абсолютное смещение его центра в проекции на ось x равно: ∆xС=∆D – SC cosα. Выразим SC через смещение SA. Для этого свяжем скорость груза А и центра масс цилиндра С: Исключая  Находим абсолютные смещения всех тел через SA и ∆D: ∆xA =∆xD-SA, ∆xB =∆xD , Связывая формулу (1) с абсолютным перемещением системы имеем: 7). Решая уравнение (7) относительно находим величину перемещения призмы 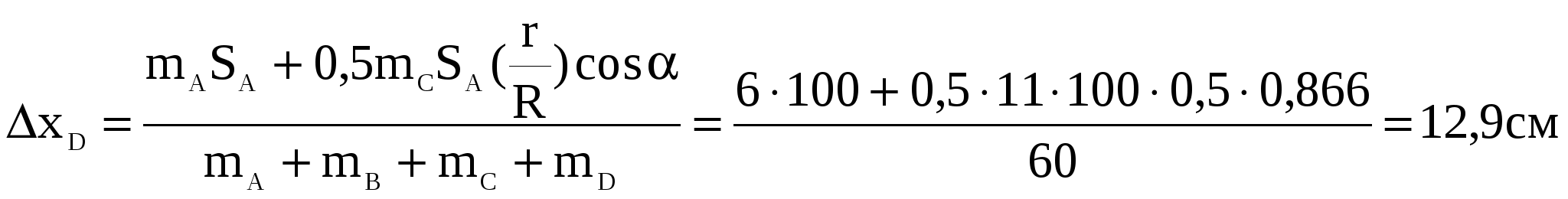 Положительное значение величины означает, что наше предположение о том, что при перемещении груза четырехугольная призма перемещается направо, оказалось верным.  Задача 4 Задача 4Механическая система состоит из тел, взаимосвязанных между собой нерастяжимой нитью. Под действием сил тяжести система из состояния покоя приходит в движение. Какую скорость приобретет груз , переместившись (вверх или вниз) на расстояние ? Качение цилиндра (или блока) происходит без проскальзывания с коэффициентом трения качения – . Коэффициент трения скольжения – . Радиусы инерции – , . Внешние радиусы – , . Внутренние радиусы – , . Кроме того, определить с каким ускорением будет двигаться груз в этот момент времени. 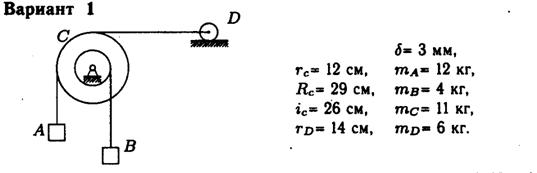 Решение Для определения скорости груза применим интегральную форму теоремы об изменении кинетической энергии механической системы: 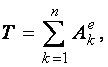 (1) (1)где: – текущее значение кинетической энергии системы; 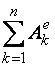 – сумма работ всех внешних сил, действующих на систему. – сумма работ всех внешних сил, действующих на систему. Зададим грузу скорость и выразим через нее скорости других точек и тел механической системы (см. рис. 1): – скорость точки блока – ; (2) – скорость груза В:   – угловая скорость блока – – угловая скорость блока – 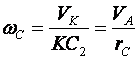 ; (3) ; (3)– скорость точки блока – 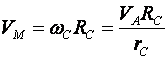 ; (4) ; (4)– скорость центра масс цилиндра – 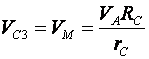 ; (5) ; (5)– угловая скорость цилиндра – 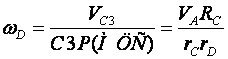 . (6) . (6)Точка контакта Р(МЦС) цилиндра с горизонтальной опорной поверхностью называется мгновенным центром скоростей (ее скорость всегда равна нулю). 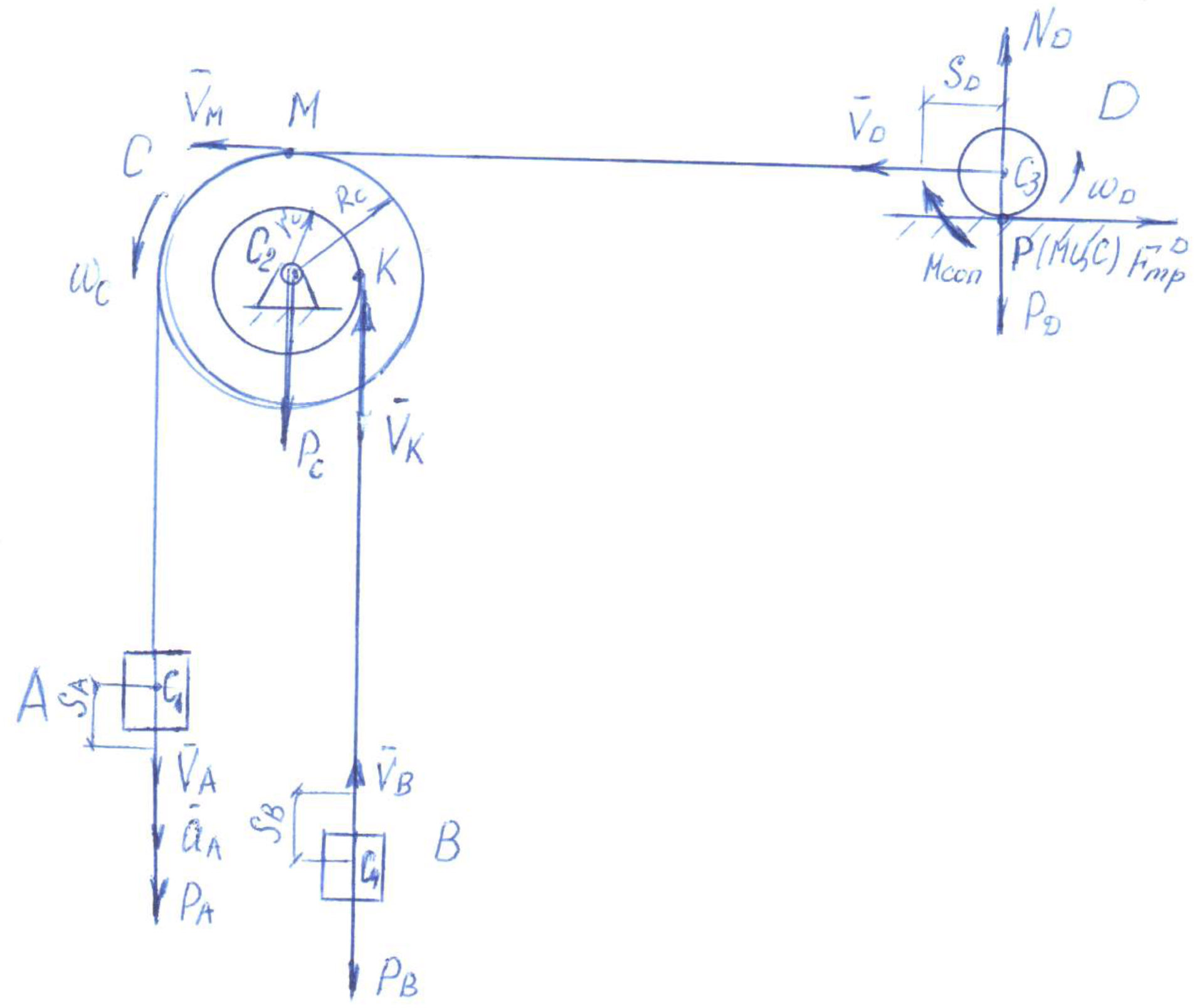 Рис. 4 3. Вычислим кинетическую энергию механической системы в виде функции от искомой скорости : где: Так как груз и В совершает поступательное движение, то его кинетическая энергия определяется по формуле: 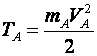 , , Так как блок совершает вращение вокруг неподвижной оси , то его кинетическая энергия определяется по формуле: 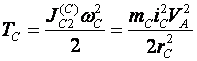 . (9) . (9)Так как цилиндр совершает плоскопараллельное движение, то его кинетическая энергия определяется по формуле: 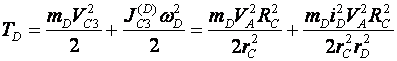 . (10) . (10)Выражения (8,9,10) подставим в (7), в результате получим окончательную формулу для вычисления кинетической энергии всей системы:  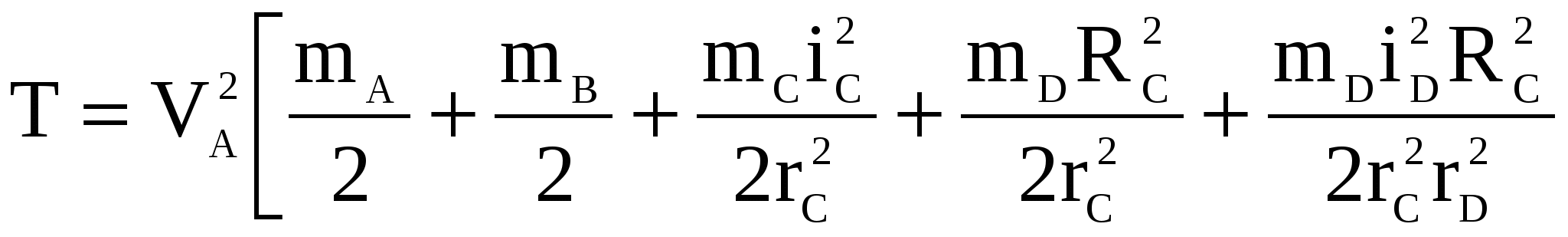 . (11) . (11)4. Вычислим сумму работ всех внешних сил, действующих на систему при заданном перемещении груза – . – работа силы тяжести груза – – работа силы тяжести груза – – работа силы тяжести блока – – работа реакции неподвижного шарнира блока – – работа силы тяжести цилиндра – – работа нормальной реакции горизонтальной опорной поверхности – – работа силы трения скольжения, действующей на цилиндр – – работа момента сопротивления качению – 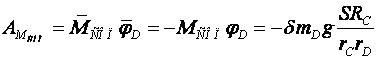 . (19) . (19)Просуммируем выражения (12–19) для получения окончательной формулы для суммарной работы всех внешних сил  5. Выражения (11) и (20) подставим в формулу (1) для определения искомой скорости. 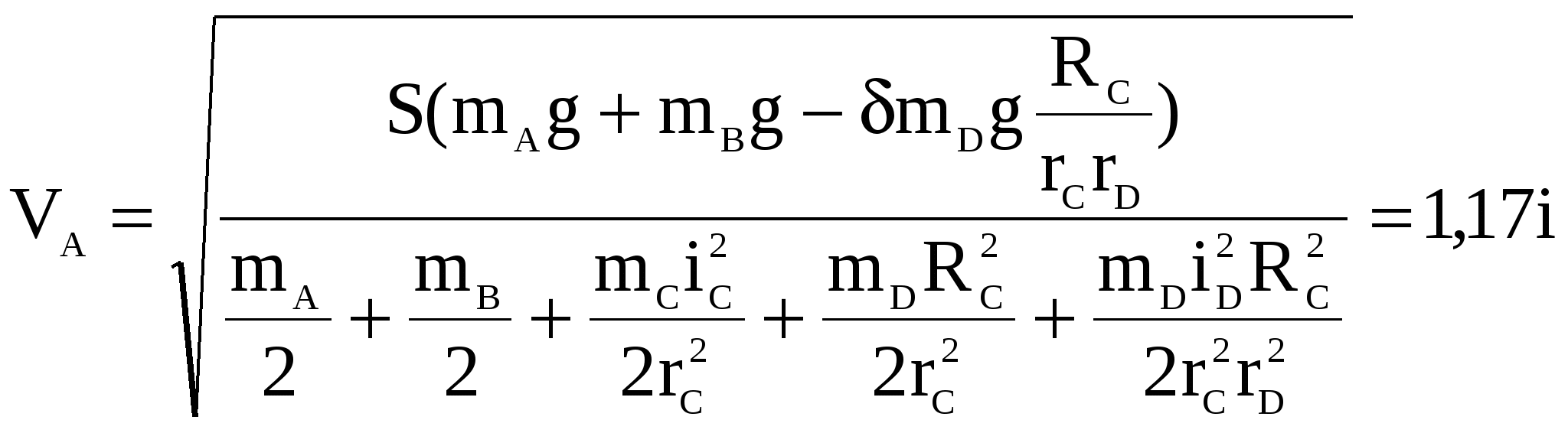 . (21) . (21)6. Для определения ускорения груза используем дифференциальную форму теоремы об изменении кинетической энергии системы 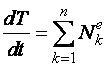 , (22) , (22)где: 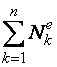 – суммарная мощность всех внешних сил, действующих на систему. – суммарная мощность всех внешних сил, действующих на систему.Выражение для суммарной мощности легко получается, если продифференцировать по времени формулу для суммарной работы этих же сил (20): так как 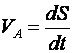 , а мощность сил по определению равна , а мощность сил по определению равна 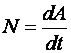 . .Теперь дифференцируем по времени выражение для кинетической энергии системы (11)  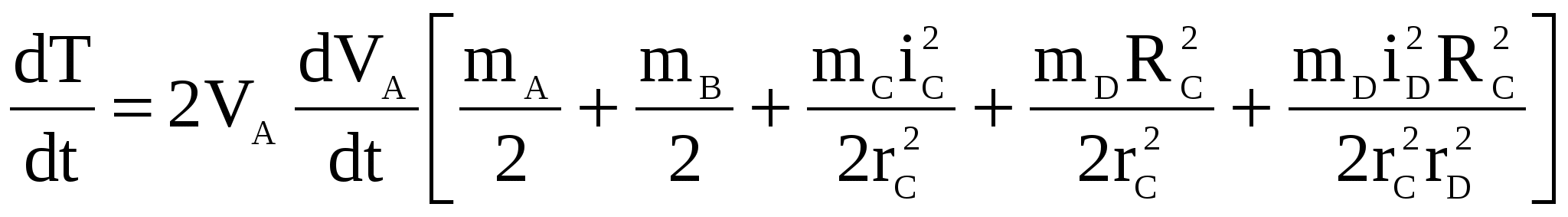 , (23) , (23)где 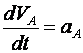 – ускорение груза. – ускорение груза.Подставляем формулы (21–22) в теорему (23) и получаем выражение для определения требуемого ускорения: 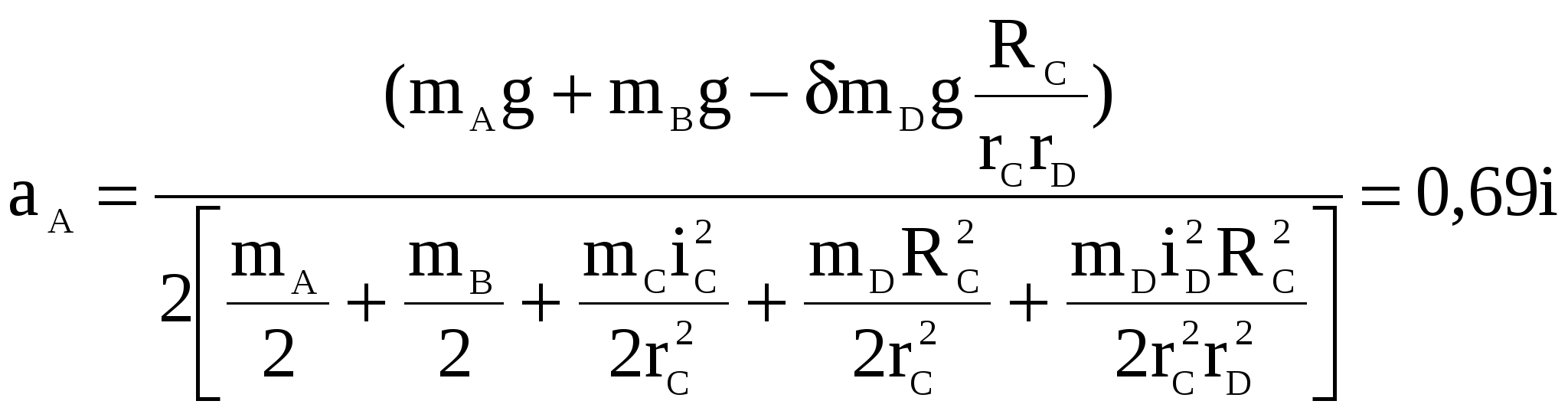  . (24) . (24)Положительное значение ускорения говорит о том, что груз движется вниз ускоренно. |
