|
|
Физика(РГЗ Теория атомов по Бору 7 Вариант). Расчётнографическое задание Формулировка задания
Расчётно-графическое задание
Формулировка задания
Атом водорода находится в возбуждённом состоянии, характеризуемом главным квантовым числом 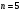 . Определите длины волн при переходе атома из возбуждённого состояния . Определите длины волн при переходе атома из возбуждённого состояния 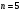 в основное. Изобразите схематически возможные переходы, соблюдая энергетический масштаб, указав численные значения энергии каждого уровня. Изобразите частотный спектр излучения. Определите радиусы стационарных орбит электрона в этих состояниях. Определите максимальную и минимальную энергии фотона в серии с наибольшим в основное. Изобразите схематически возможные переходы, соблюдая энергетический масштаб, указав численные значения энергии каждого уровня. Изобразите частотный спектр излучения. Определите радиусы стационарных орбит электрона в этих состояниях. Определите максимальную и минимальную энергии фотона в серии с наибольшим  . Как называется эта серия? Определите работу ионизации атома, т. е. полного удаления электрона с заданной орбиты. Каково изменение скорости атома при переходе электрона с заданной орбиты . Как называется эта серия? Определите работу ионизации атома, т. е. полного удаления электрона с заданной орбиты. Каково изменение скорости атома при переходе электрона с заданной орбиты 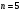 на орбиту на орбиту 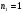 , а также изменение при этом момента импульса электрона. Вычислите минимальную разрешающую способность спектрального прибора для разрешения всех линий серии с максимальным , а также изменение при этом момента импульса электрона. Вычислите минимальную разрешающую способность спектрального прибора для разрешения всех линий серии с максимальным  . Определите скорость, с которой электрон движется по 5 орбите атома. Определите потенциальную, кинетическую и полную энергии электрона в атоме в заданном возбуждённом состоянии . Определите скорость, с которой электрон движется по 5 орбите атома. Определите потенциальную, кинетическую и полную энергии электрона в атоме в заданном возбуждённом состоянии 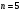 . Определите орбитальные магнитные моменты электрона, движущегося на всех орбитах, начиная с пятой по первую. . Определите орбитальные магнитные моменты электрона, движущегося на всех орбитах, начиная с пятой по первую.
Краткое теоретическое содержание
Для атома водорода формула, описывающая спектральные линии, подобрана экспериментально и называется формулой Бальмера – в честь учёного, впервые получившего ее для спектрального диапазона видимого излучения. Схема переходов приведена на рис.1.
Длины волн излучаемых атомом водорода определяются по формуле:
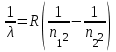 , (1) , (1)
где 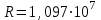 м-1 – постоянная Ридберга; м-1 – постоянная Ридберга;  и и 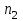 – главные квантовые числа, соответствующие энергетическим уровням, между которыми совершается электронный переход в атоме. Длина волн излучаемых водородоподобными ионами с зарядовым числом ядра Z (число Z определяется по номеру химического элемента в таблице Менделеева), могут быть рассчитаны по формуле: – главные квантовые числа, соответствующие энергетическим уровням, между которыми совершается электронный переход в атоме. Длина волн излучаемых водородоподобными ионами с зарядовым числом ядра Z (число Z определяется по номеру химического элемента в таблице Менделеева), могут быть рассчитаны по формуле:
 . (2) . (2)
Водородоподобными ионами называют атомы с одним электроном на внешней оболочке.
Рентгеновское излучение возникает при переходах на внутренних оболочках. Частоты и длины волн соответствующего излучения можно определить, используя закон Мозли:
 , (3) , (3)
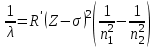 , (4) , (4)
где Z – порядковый номер элемента в системе Менделеева, R и R' – постоянные Ридберга для частот и длин волн (R= 3,29 ∙ 1015 c-1 и R' = 1,10 ∙ 107 м-1), n1 – номер уровня, с которого переходит электрон, n2 – номер уровня, на который переходит электрон. Величина σучитывает экранировку внутренними электронами Кулоновского взаимодействия ядра и рассматриваемого электрона и называется постоянной экранирования.
Правила отбора для электромагнитных переходов:
Δj= 0, ±1; Δmj = 0, ±1; Δℓ = ±1; Δmℓ = 0, ±1; Δms= 0.
Первый постулат Бора (постулат стационарных состояний): в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии.
Второй постулат Бора (правило частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией
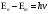 (5). (5).
Фотон — элементарная частица, квант электромагнитного излучения. Это безмассовая частица, способная существовать только двигаясь со скоростью света.
Энергия фотона — это энергия элементарной частицы (фотона), квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света.
 . .
О дин электрон-вольт равен энергии, которая необходима для переноса электрона в электростатическом поле между точками с разницей потенциалов в 1В. Так как работа при переносе заряда q равна qU (где U — разность потенциалов), а заряд электрона составляет −1,6·10−19 Кл, то 1 эВ = 1,6·10−19 Дж . дин электрон-вольт равен энергии, которая необходима для переноса электрона в электростатическом поле между точками с разницей потенциалов в 1В. Так как работа при переносе заряда q равна qU (где U — разность потенциалов), а заряд электрона составляет −1,6·10−19 Кл, то 1 эВ = 1,6·10−19 Дж .
Наиболее вероятное расстояние электрона в состоянии n от ядра:
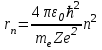 , (6) , (6)
где me – масса электрона, Z– заряд ядра (атомный номер), n= 1, 2, 3… – главные квантовые числа. При n= 1 и Z= 1 это расстояние совпадает с радиусом первой боровской орбиты.
Одновременное измерение модуля момента импульса и трёх его проекций на оси координат в квантовой механике невозможно. Модуль момента импульса определяется:
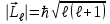 . (7) . (7)
Число ℓ = 0, 1, 2, …, n-1 называется орбитальным квантовым числом.
Проекция момента импульса на любую ось (z) тоже может принимать лишь определённые значения
 , (8) , (8)
где mℓ = 0, ± 1, ± 2, …, ± ℓ и называется магнитным квантовым числом. Такое название связано с тем, что оно определяет также проекцию магнитного момента, создаваемого движением электрона вокруг ядра:
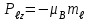 . (9) . (9)
Модуль магнитного момента электрона
 , (10) , (10)
где  = 0,927∙10-23 Дж/Тл – магнетон Бора. = 0,927∙10-23 Дж/Тл – магнетон Бора.
Квантовые значения энергии электрона в водородоподобном атоме:
 , (11) , (11)
n=1, 2, 3, … - главное квантовое число.
Решение поставленных задач
Для определения длины волн при переходе атома из возбуждённого состояния 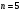 в основное в основное 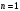 используем формулу (4). С этой формулы получим используем формулу (4). С этой формулы получим
 , где , где 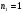 , , 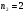 . .
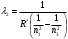 , где , где 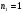 , , 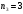 . .
 , где , где 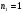 , ,  . .
 ; ; 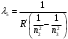 ; ; 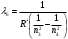 ; ; 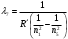 ; ; 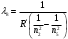 ; ;  ; ; 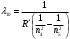 . .
Проверка размерности:  . .
Расчёты
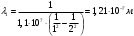 ; ; 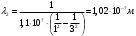 ; ; ; ;  ; ;  ; ;  ; ;  ; ; 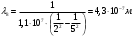 ; ;
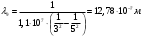 ; ; 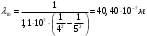 . .
Изобразим схематически возможные переходы, соблюдая энергетический масштаб, указав численные значения энергии каждого уровня.
Квантовые значения энергии электрона в водородоподобном атоме определяются по формуле (11). С этой формулы
 . .
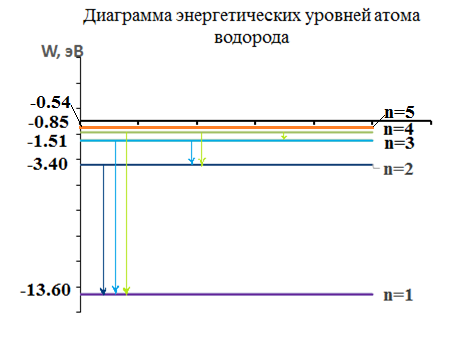
Изобразим частотный спектр излучения.

Определим радиусы стационарных орбит электрона в состояниях 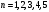 . При этом воспользуемся формулой (6): . При этом воспользуемся формулой (6):
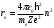 . .
Проверка размерности:
 . .
Расчёт:
 ; ;
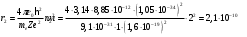 ; ;
 . .
 . .

Определим максимальную и минимальную энергии фотона в серии с наибольшим  ( в моем случае для серии Брекетта ). Исходя их формул (3) и (5) находим ( в моем случае для серии Брекетта ). Исходя их формул (3) и (5) находим
 , где , где  и и
 , где , где 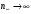 . .
Проверка размерности:  . .
Расчёт: 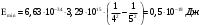 ; ;
 . .
Определим работу ионизации атома, т. е. полного удаления электрона с заданной орбиты  в бесконечность. То есть, исходя их формул (3) и (5) находим что в бесконечность. То есть, исходя их формул (3) и (5) находим что 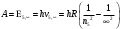 . .
Проверка размерности:  . .
Расчёт: 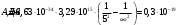 . .
Определим изменение скорости атома при переходе электрона с заданной орбиты 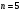 на орбиту на орбиту 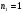 , а также изменение при этом момента импульса электрона. Пользуясь теорией Бора находим скорость электрона на n-ой орбите: , а также изменение при этом момента импульса электрона. Пользуясь теорией Бора находим скорость электрона на n-ой орбите:
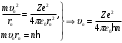 . .
Тогда изменение скорости при переходе электрона с заданной орбиты 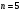 на орбиту на орбиту 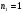 будет равно будет равно 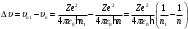
Проверка размерности:  . .
Расчёт: 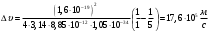 . .
Пользуясь формулой (7) находим изменение момента импульса электрона:
 , где , где 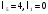 . .
Проверка размерности: 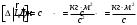 . .
Тогда
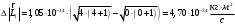 . .
Вычислим минимальную разрешающую способность спектрального прибора для разрешения всех линий серии Брекетта.
Так как разрешающая способность спектрального прибора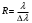 , то минимальная разрешающая способность для серии Брекета , то минимальная разрешающая способность для серии Брекета
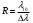 , где , где
Проверка размерности:  - безразмерная величина. - безразмерная величина.
Расчёт:  . .
Определим скорость, с которой электрон движется по 5-ой орбите атома.
Пользуясь формулой, выведенной в пункте 7 находим искомую скорость 
Проверка размерности:  . .
Расчёт: 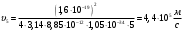 . .
Определим потенциальную, кинетическую и полную энергии электрона в атоме в заданном возбуждённом состоянии 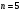 . .
Пользуясь теорией Бора находим скорость электрона на n-ой орбите:
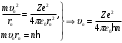 . Тогда кинетическая энергия электрона . Тогда кинетическая энергия электрона
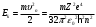 . Полная энергия электрона . Полная энергия электрона 
Потенциальная энергия равна 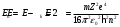 . .
Расчёты: 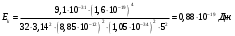 ; ;
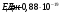 ; ; 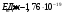 . .
Определим орбитальные магнитные моменты электрона, движущегося на всех орбитах, начиная с 5-ой по первую.
Воспользуемся формулой (10)
 , ,
где  = 0,927∙10-23 Дж/Тл – магнетон Бора. = 0,927∙10-23 Дж/Тл – магнетон Бора.
На пятой орбите:
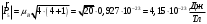 . .
На четвертой орбите:
 . .
На третей орбите:
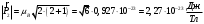 . .
На второй орбите:
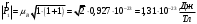 . .
На первой орбите:
 . . |
|
|
 Скачать 288.43 Kb.
Скачать 288.43 Kb.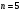 . Определите длины волн при переходе атома из возбуждённого состояния
. Определите длины волн при переходе атома из возбуждённого состояния 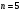 в основное. Изобразите схематически возможные переходы, соблюдая энергетический масштаб, указав численные значения энергии каждого уровня. Изобразите частотный спектр излучения. Определите радиусы стационарных орбит электрона в этих состояниях. Определите максимальную и минимальную энергии фотона в серии с наибольшим
в основное. Изобразите схематически возможные переходы, соблюдая энергетический масштаб, указав численные значения энергии каждого уровня. Изобразите частотный спектр излучения. Определите радиусы стационарных орбит электрона в этих состояниях. Определите максимальную и минимальную энергии фотона в серии с наибольшим  . Как называется эта серия? Определите работу ионизации атома, т. е. полного удаления электрона с заданной орбиты. Каково изменение скорости атома при переходе электрона с заданной орбиты
. Как называется эта серия? Определите работу ионизации атома, т. е. полного удаления электрона с заданной орбиты. Каково изменение скорости атома при переходе электрона с заданной орбиты 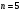 на орбиту
на орбиту 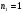 , а также изменение при этом момента импульса электрона. Вычислите минимальную разрешающую способность спектрального прибора для разрешения всех линий серии с максимальным
, а также изменение при этом момента импульса электрона. Вычислите минимальную разрешающую способность спектрального прибора для разрешения всех линий серии с максимальным  . Определите скорость, с которой электрон движется по 5 орбите атома. Определите потенциальную, кинетическую и полную энергии электрона в атоме в заданном возбуждённом состоянии
. Определите скорость, с которой электрон движется по 5 орбите атома. Определите потенциальную, кинетическую и полную энергии электрона в атоме в заданном возбуждённом состоянии 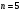 . Определите орбитальные магнитные моменты электрона, движущегося на всех орбитах, начиная с пятой по первую.
. Определите орбитальные магнитные моменты электрона, движущегося на всех орбитах, начиная с пятой по первую.
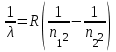 , (1)
, (1)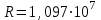 м-1 – постоянная Ридберга;
м-1 – постоянная Ридберга;  и
и 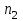 – главные квантовые числа, соответствующие энергетическим уровням, между которыми совершается электронный переход в атоме. Длина волн излучаемых водородоподобными ионами с зарядовым числом ядра Z (число Z определяется по номеру химического элемента в таблице Менделеева), могут быть рассчитаны по формуле:
– главные квантовые числа, соответствующие энергетическим уровням, между которыми совершается электронный переход в атоме. Длина волн излучаемых водородоподобными ионами с зарядовым числом ядра Z (число Z определяется по номеру химического элемента в таблице Менделеева), могут быть рассчитаны по формуле: . (2)
. (2) , (3)
, (3)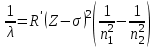 , (4)
, (4)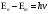 (5).
(5). дин электрон-вольт равен энергии, которая необходима для переноса
дин электрон-вольт равен энергии, которая необходима для переноса 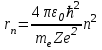 , (6)
, (6)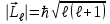 . (7)
. (7) , (8)
, (8)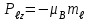 . (9)
. (9) , (10)
, (10) = 0,927∙10-23 Дж/Тл – магнетон Бора.
= 0,927∙10-23 Дж/Тл – магнетон Бора. , (11)
, (11)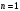 используем формулу (4). С этой формулы получим
используем формулу (4). С этой формулы получим , где
, где 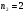 .
.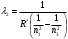 , где
, где 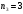 .
. , где
, где  .
. ;
; 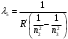 ;
; 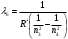 ;
; 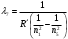 ;
; 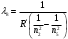 ;
;  ;
; 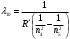 .
. .
.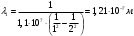 ;
; 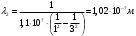 ;
; ;
;  ;
;  ;
;  ;
;  ;
; 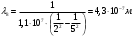 ;
;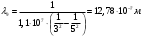 ;
; 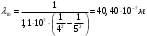 .
. .
.

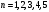 . При этом воспользуемся формулой (6):
. При этом воспользуемся формулой (6):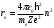 .
. .
. ;
;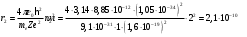 ;
; .
. .
.
 , где
, где  и
и , где
, где 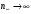 .
. .
.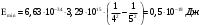 ;
; .
. в бесконечность. То есть, исходя их формул (3) и (5) находим что
в бесконечность. То есть, исходя их формул (3) и (5) находим что 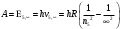 .
.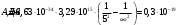 .
.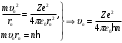 .
.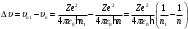
 .
.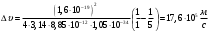 .
. , где
, где 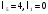 .
. 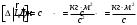 .
.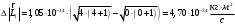 .
.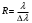 , то минимальная разрешающая способность для серии Брекета
, то минимальная разрешающая способность для серии Брекета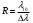 , где
, где  - безразмерная величина.
- безразмерная величина. .
.
 .
.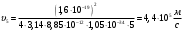 .
.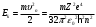 . Полная энергия электрона
. Полная энергия электрона 
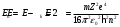 .
.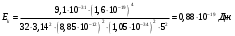 ;
;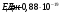 ;
; 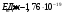 .
.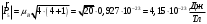 .
. .
.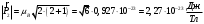 .
.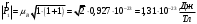 .
. .
.