Лабораторная работа 4. Расход по расходомерной
 Скачать 148.57 Kb.
|
|
Определяю расход по расходомерной диафрагме 𝐻 = ℎ2 − ℎ1 𝐻1 = 0,62 − 0,6 = 0,02 м 𝐻2 = 0,67 − 0,63 = 0,04 м 𝐻3 = 0,69 − 0,64 = 0,05 м 𝐻4 = 0,67 − 0,63 = 0,04 м 𝐻5 = 0,66 − 0,62 = 0,04 м 𝐻6 = 0,68 − 0,64 = 0,04 м 𝐻7 = 0,70 − 0,65 = 0,05 м 𝐻8 = 0,69 − 0,65 = 0,04 м Измерим с помощью линейки по графику (1 условная единица = 1 мм на чертеже): Если 81 единица – 200 мм То тогда х единиц – 20 мм  81 𝑥 81 ∙ 20  200 = 20 ⇒ 𝑥 =200 = 8,1 единиц Отложив значение Н на графике в масштабе с помощью линейки, получим значение Q в единицах Если 61 единица – 0,2 л/с То тогда 49 единиц – х л/с 61  0,2 =49 𝑥 ⇒ 𝑥 =0,2 ∙ 49  61 = 0,16 л м3  = 1,6 ∙ 10−4 с с Аналогично м3 𝑄1 = 1,6 ∙ 10−4 с Если 81 единица – 200 мм То тогда х единиц – 40 мм 81 𝑥 81 ∙ 40 200 = 40 ⇒ 𝑥 =Если 61 единица – 0,2 л/с То тогда 72 единицы – х л/с 200 = 16,2 единиц 61 0,2 =72 𝑥 ⇒ 𝑥 =0,2 ∙ 72 61 = 0,24 л м3 = 2,4 ∙ 10−4 с с м3 𝑄2 = 2,4 ∙ 10−4 с м3 𝑄2 = 𝑄3 = 𝑄4 = 𝑄5 = 2,4 ∙ 10−4 с Если 81 единица – 200 мм То тогда х единиц – 30 мм 81 𝑥 81 ∙ 30 200 = 30 ⇒ 𝑥 =Если 61 единица – 0,2 л/с 200 = 12,2 единиц То тогда 61 единица – также 0,2 л/с м3 𝑄6 = 2 ∙ 10−4с м3 𝑄6 = 𝑄7 = 2 ∙ 10−4с Если 81 единица – 200 мм То тогда х единиц – 10 мм 81 𝑥 81 ∙ 10 200 = 10 ⇒ 𝑥 =Если 61 единица – 0,2 л/с То тогда 36 единиц – х л/с 200 = 4,1 единиц 61 0,2 =36 𝑥 ⇒ 𝑥 =0,2 ∙ 36 61 = 0,12 л м3 = 1,2 ∙ 10−4 с с м3 𝑄8 = 1,2 ∙ 10−4 с Определяю среднюю скорость движения воды в трубопроводе 4 ∙ 𝑄  𝑉 = 𝜋 ∙ 𝑑24 ∙ 1,6 ∙ 10−4  𝑉1 = 𝜋 ∙ 0,022 = 0,509 м/с𝑉2 = 𝑉3 = 𝑉4 = 𝑉5 = 4 ∙ 2,4 ∙ 10−4 𝜋 ∙ 0,022 = 0,764 м/с𝑉6 = 𝑉7 = 4 ∙ 2 ∙ 10−4  𝜋 ∙ 0,022 = 0,637 м/с𝑉8 = 4 ∙ 1,2 ∙ 10−4 𝜋 ∙ 0,022 = 0,382 м/сОпределяю по формуле Пуазейля кинематическую вязкость воды 0,0178  𝜈 = 1 + 0,6337 ∙ 𝑡 + 0,000221 ∙ 𝑡20,0178  𝜈 = 1 + 0,6337 ∙ 20 + 0,000221 ∙ 202= 1,29 ∙ 10−3 Ст 𝜈 = 1,29 ∙ 10−3 Ст = 1,29 ∙ 10−7 м2/с Определяю число Рейнольдса 𝑅𝑒 = 𝑉 ∙ 𝑑  𝜈 𝑅𝑒1 = 0,509 ∙ 0,02  1,29 ∙ 10−7 = 79000𝑅𝑒2 = 𝑅𝑒3 = 𝑅𝑒4 = 𝑅𝑒5 = 0,764 ∙ 0,02 1,29 ∙ 10−7 = 118501𝑅𝑒6 = 𝑅𝑒7 = 0,637 ∙ 0,02 1,29 ∙ 10−7 = 98751𝑅𝑒8 = 0,382 ∙ 0,02 1,29 ∙ 10−7 = 59251Определяю потери напора по длине ℎ𝐼 ℎ𝐼 = ℎ3 − ℎ4 1)ℎ𝐼 = 0,56 − 0,5 = 0,06 м 2)ℎ𝐼 = 0,59 − 0,54 = 0,05 м 3)ℎ𝐼 = 0,61 − 0,57 = 0,04 м 4)ℎ𝐼 = 0,60 − 0,55 = 0,05 м 5)ℎ𝐼 = 0,58 − 0,53 = 0,05 м 6)ℎ𝐼 = 0,60 − 0,56 = 0,04 м 7)ℎ𝐼 = 0,62 − 0,59 = 0,03 м 8)ℎ𝐼 = 0,61 − 0,57 = 0,04 м Определяю опытное значение коэффициента гидравлического трения 𝜆оп = ℎ𝐼 ∙ 2𝑔𝑑  𝑉2 ∙ 𝑙𝜆оп1 = 0,06 ∙ 2 ∙ 9,81 ∙ 0,02  0,5092 ∙ 0,65 = 0,14𝜆оп2 = 𝜆оп3 = 𝜆оп4 = 𝜆оп5 = 0,05 ∙ 2 ∙ 9,81 ∙ 0,02 0,7642 ∙ 0,65 = 0,0520,04 ∙ 2 ∙ 9,81 ∙ 0,02 0,7642 ∙ 0,65 = 0,0410,05 ∙ 2 ∙ 9,81 ∙ 0,02 0,7642 ∙ 0,65 = 0,0520,05 ∙ 2 ∙ 9,81 ∙ 0,02 0,7642 ∙ 0,65 = 0,052 0,04 ∙ 2 ∙ 9,81 ∙ 0,02𝜆оп6 = 0,6372 ∙ 0,65 = 0,041 𝜆оп7 = 𝜆оп8 = 0,03 ∙ 2 ∙ 9,81 ∙ 0,02 0,6372 ∙ 0,65 = 0,0310,04 ∙ 2 ∙ 9,81 ∙ 0,02 0,3822 ∙ 0,65 = 0,041Определяю расчетные значения коэффициента гидравлического трения 10𝑑 𝑅𝑒пр1 = ∆10 ∙ 0,02  𝑅𝑒пр1 = 0,00001 = 20000500𝑑  𝑅𝑒пр2 = ∆𝑅𝑒пр2 = 500 ∙ 0,02  0,00001 = 100000𝑅𝑒пр1 < 𝑅𝑒 < 𝑅𝑒пр2 зона смешанного трения, используем формулу Альштуля 68 ∆ 0,25 𝜆 = 0,11 ∙ (𝑅𝑒 + 𝑑)68  𝜆1 = 0,11 ∙ (79000 +0,01  20 )0,25 = 0,021 68  𝜆2 = 0,11 ∙ (118501 +68 𝜆3 = 0,11 ∙ (118501 +68 𝜆4 = 0,11 ∙ (118501 +68 𝜆5 = 0,11 ∙ (118501 +0,01 20 )0,01 20 )0,01 20 )0,01 20 )0,25 0,25 0,25 0,25 = 0,02 = 0,02 = 0,02 = 0,02 68 𝜆6 = 0,11 ∙ (98751 +68 𝜆7 = 0,11 ∙ (98751 +68 𝜆8 = 0,11 ∙ (59251 +0,01 20 )0,01 20 )0,01 20 )0,25 0,25 0,25 = 0,020 = 0,020 = 0,022 8. График зависимости 𝑙𝑔100𝜆 = 𝑓(𝑙𝑔𝑅𝑒) 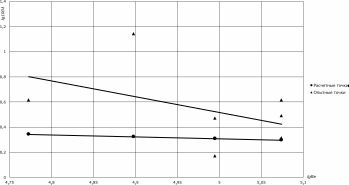 9. Среднее квадратическое 𝜆оп и 𝜆ращ ∑𝑛 𝑥2 𝑆 = √𝑖=1 𝑖 𝑛  𝑆(𝜆оп) = 0,142 + 0,0522 + 0,0412 + 0,0522 + 0,0522 + 0,0412 + 0,0312 + 0,0412 = √ =8 = 0,065  𝑆(𝜆ращ) = √0,0212 + 0,022 + 0,022 + 0,022 + 0,022 + 0,0202 + 0,0202 + 0,0222 = 8 = = 0,020 |