Раскраски. 6. Волчёнков С.Г. Раскраски. Раскраски Приведите пример правильной раскраски в 4 цвета карты, изображенной на рисунке справа 2
 Скачать 37.53 Kb.
|
|
Раскраски 1 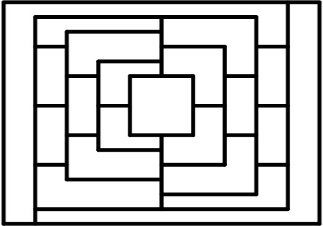 . Приведите пример правильной раскраски в 4 цвета карты, изображенной на рисунке справа? 2. Можно ли обойтись тремя цветами? 3. На плоскости нарисовано несколько равносторонних треугольников. Они не пересекаются, но могут иметь общие участки сторон. Найдите наименьшее количество цветов, которых хватит для их правильной раскраски. 4. Многоугольник разбит на треугольные области (триангулирован). Каждые две граничащие друг с другом области имеют целую общую сторону (т.е. вершина одного треугольника не лежит на стороне другого). Докажите, что все области допускают правильную раскраску тремя цветами. 5. На плоскости нарисовано несколько треугольников (не обязательно правильных). Они не пересекаются, но могут иметь общие участки сторон. Найдите наименьшее количество цветов, которых хватит для их правильной раскраски. 6. Плоскость разбита на части прямыми и окружностями. Докажите, что получившуюся карту можно правильно раскрасить в два цвета. 7. Можно ли разместить на плоскости несколько одинаковых непересекающихся по внутренним точкам квадратов, которые нельзя правильно раскрасить в три цвета? 8. Разместите на поверхности тора пять областей, касающихся друг друга по участкам границ. 9. Прямая раскрашена в два цвета. Докажите, что найдётся отрезок, оба конца и середина которого покрашены в один и тот же цвет. 10. Плоскость покрашена в 2 цвета. Докажите, что найдутся 2 точки одного цвета на расстоянии 1. 11. Плоскость покрашена в 2 цвета. Докажите, что найдутся 2 точки разных цветов на расстоянии 1. 12. Некоторые клетки белого прямоугольника размером 3×7 произвольным образом покрасили в чёрный цвет. Докажите, что обязательно найдутся четыре клетки одного цвета, центры которых являются вершинами некоторого прямоугольника со сторонами, параллельными сторонам исходного прямоугольника. 13. Бесконечная клетчатая плоскость раскрашена в три цвета. Докажите, что найдутся четыре точки одного цвета, расположенные в вершинах прямоугольника. 14. Точки сторон правильного треугольника раскрашены в два цвета. Докажите, что найдётся прямоугольный треугольник с вершинами одного цвета. 15. Все точки плоскости покрашены в один из N цветов. Каждая прямая проходит через точки не более чем двух цветов. При каком наибольшем N это возможно? 16. Все точки плоскости покрашены в один из двух цветов. Докажите, что найдётся равносторонний треугольник с вершинами одного цвета. 17. Все точки плоскости покрашены в один из трёх цветов. Докажите, что найдётся равносторонний треугольник с вершинами одного цвета. 18. Докажите, что хроматическое число прямой равно 2. 19. Докажите, что хроматическое число плоскости больше 3. 20. Докажите, что хроматическое число плоскости меньше 10. 21. Докажите, что хроматическое число плоскости меньше 9. 22. Докажите, что хроматическое число плоскости меньше 8. |