СПЕКТР АТОМА ВОДОРОДА» и «РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОННОЙ ПЛОТНОСТИ АТОМА ВОДОРОДА. Распределение электронной плотности атома водорода

• Название: Распределение электронной плотности атома водорода
• Анкор: СПЕКТР АТОМА ВОДОРОДА» и «РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОННОЙ ПЛОТНОСТИ АТОМА ВОДОРОДА
• Дата: 15.12.2022
• Размер: 302.9 Kb.
• Имя файла: lab_3 (1).docx
• Тип: Лабораторная работа; #847124

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет радиофизики и компьютерных технологий

Лабораторные работы №3+5

«СПЕКТР АТОМА ВОДОРОДА» и «РАСПРЕДЕЛЕНИЕ ЭЛЕКТРОННОЙ ПЛОТНОСТИ АТОМА ВОДОРОДА»

Выполнил: Крицкий А.О., 3 курс, 6+7 ПИ

Преподаватель: Прокопович И.П.

Минск, 2022

Лабораторная работа №3

Цель работы: Для атома водорода определить экспериментально длины волн первых трех спектральных линий (H_α, H_β, H_γ) в серии Бальмера; вычислить значение постоянной Ридберга

Краткая теория
И
зучение атомных спектров послужило ключом к познанию строения атома. Прежде всего было замечено, что линии в спектрах атомов располагаются не беспорядочно, а группируется в так на­зываемые серии. Отчетливее всего это обнаруживается в спектре атома водорода, изображенном на рис. 3.1.

Очевидно, что линии располагаются в определенном порядке в виде серий, а расстояние между линиями в каждой серии закономерно убывает по мере перехода от более длинных волн кболее коротким. Швейцарский физик И. Бальмер обнаружил (1885 г.), что длины волн линий водорода могут быть точно представлены формулой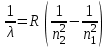

(3.1)

или при переходе от длины волны к частоте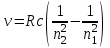

, (3.2)

где R = 109737 см^–1 эмпирическая постоянная, называемая постоянной Ридберга; с  скорость света в вакууме.

С помощью формул (3.1) и (3.2) можно получить λ или  любой линии в любой серии. Так, если положить n₂ = 1, а величине n₁ придавать значения 2, 3, 4,... то получим длины волн (частоты) линий в серии Лаймана. Аналогично, линии остальных серий получаются при следующих значениях n₂ и n₁:

серия Лаймана: n₂ = 1, n₁ = 2, 3, 4 ... (ультрафиолетовая область).

серия Бальмера: n₂ = 2, n₁ = 3, 4, 5 .. (видимая область)

серия Пашена: n₂ = 3, n₁ = 4, 5, 6... (инфракрасная область)

серия Брэкета: n₂ = 4, n₁ = 5, 6, 7… (инфракрасная область)

серия Пфунда: n₂ = 5, n₁ = 6, 7, 8 ... (инфракрасная область)

Экспериментальная установка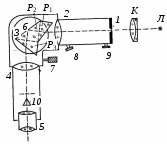



Рис. 1

Свет от источника Л конденсоромK собирается на входной

щели 1 монохроматора УМ-2. Входная щель снабжена микрометрическим винтом 9, который позволяет открывать щель на нужную ширину. Обычная рабочая ширина щели равна 0,02 – 0,03 мм. Коллиматорный объектив 2 снабжен микрометрическим винтом 8. С помощью винта можно смещать объектив относительно щели при фокусировке спектральных линий различных цветов. Объективом 2 излучение источника направляется на сложную призму 3, установленную на поворотном столике 6. Первые две призмы P₁ и P₂ с преломляющими углами 30 изготовлены из тяжелого флинта, обладающего большой дисперсией. Промежуточная призма P₃ сделана из крона. Лучи отражаются от ее гипотенузной грани и поворачиваются на 90. Благодаря такому устройству дисперсии призм P₁ и P₂ складываются. При помощи микрометрического винта с отсчетным барабаном 7 поворотный столик 6 вращается вокруг вертикальной оси. На барабан нанесена винтовая дорожка с градусными делениями. Вдоль дорожки скользит указатель поворота барабана. При вращении барабана призма поворачивается, и в центре поля зрения появляются различные участки спектра.

Результаты измерений

1. 
   Первые три спектральные линии серии Бальмера (n₂ = 2), при R = 1,09737 * 10⁷ м^-1
   

• 
  При n₁ = 3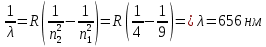
  

• 
  При n₁ = 4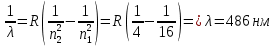
  

• 
  При n₁ = 5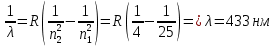
  

2. 
   Экспериментальное определение длины волны водородных линий H_α, H_β, H_γ в видимой области спектра
   

волна	цвет	угол поворота барабана, °	λ,	λ, нм (практ)	λ, нм (теор)
Hα	красный	2772	6600	660	656
Hβ	сине-зеленый	1732	4950	495	486
Hγ	фиолетовый	1598	4530	453	433

Таблица 1

3. 
   Вычисления среднего значения Ридберга по значениям, полученным в ходе работы: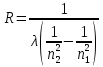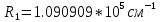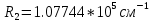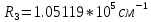
   

< R > =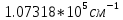

Вывод: Теоретическое значение постоянной Ридберга (R_теор = 1,09737*10⁵ см^-1) немного отличается от среднего значения постоянных, полученных нами для водородных линий H_α, H_β, H_γ (< R > = 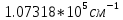). Такой результат может быть следствием возможного попадания на щель монохроматора солнечного света, приборной погрешности, возможной неточностью градуировочного графика и другими факторами.

Лабораторная работа №5

Цель работы: рассчитать распределение радиальной электронной плотности вероятности в различных состояниях для атома водорода.

Краткая теория

Состояние некоторой частицы в квантовой (волновой) механике задаётся так называемой волновой функцией 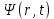. Её вид получается из решения уравнения Шрёдингера: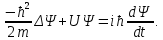



Для нахождения волновой 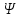функции необходимо записать вид функции 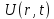для данной конкретной задачи и решить уравнение Шредингера относительно 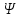. Если силовое поле, в котором движется частица, стационарно, то уравнение Шредингера примет вид: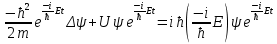



и решение 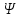можно представить в виде двух сомножителей:

.

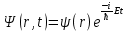Потенциальная энергия водорода не зависит от времени и равно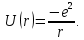



Волновые функции состояний атома водорода: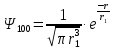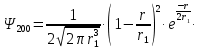





Радиальная плотность вероятности вычисляется следующим образом: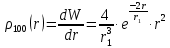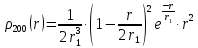





Ход работы

1. 
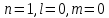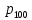   Для состояния распределение плотности вероятности выглядит следующим образом:
   

Плотность вероятности ρ₁₀₀(r)

r,Å

ρ,Å^-1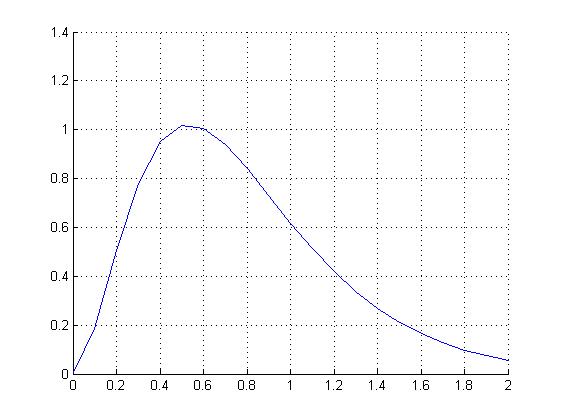

2. 
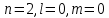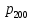   Для состояния распределение плотности вероятности выглядит следующим образом :
   

Плотность вероятности ρ₂₀₀(r)

ρ,Å^-1

r,Å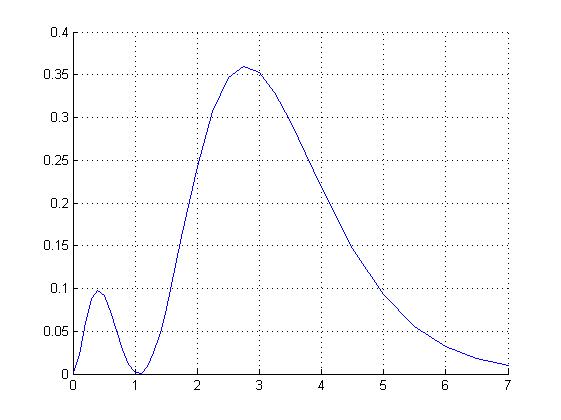

Вывод: Из графиков видно, что для атома водорода находящегося в основном состоянии, наиболее вероятное удаление электрона от ядра соответствует первому боровскому радиусу, в то время как для квантового состояния 200 характерно наиболее вероятное радиальное положение электрона около 2,7Å от ядра, но так же электрон может оказаться на расстоянии первого боровского радиуса.

^{Ответы на контрольные вопросы по лабораторной работе № 3}

1. Каковы закономерности спектра атома водорода?

Очевидно, что линии располагаются в определенном порядке в виде серий, а расстояние между линиями в каждой серии закономерно убывает по мере перехода от более длинных волн к более коротким. Швейцарский физик И. Бальмер обнаружил (1885 г.), что длины волн линий водорода могут быть точно представлены формулой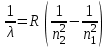



где R = 109737 см^–1 эмпирическая постоянная, называемая постоянной Ридберга; с  скорость света в вакууме.

Так, если положить n₂ = 1, а величине n₁ придавать значения 2, 3, 4,... то получим длины волн линий в серии Лаймана:

серия Лаймана: n₂ = 1, n₁ = 2, 3, 4 ... (ультрафиолетовая область).

Аналогично, линии остальных серий получаются при следующих значениях n₂ и n₁:

серия Бальмера: n₂ = 2, n₁ = 3, 4, 5 .. (видимая область)

серия Пашена: n₂ = 3, n₁ = 4, 5, 6... (инфракрасная область)

серия Брэкета: n₂ = 4, n₁ = 5, 6, 7… (инфракрасная область)

серия Пфунда: n₂ = 5, n₁ = 6, 7, 8 ... (инфракрасная область)

2. В чем заключаются постулаты Бора?

Атомы могут пребывать только в определенных стационарных состояниях, в которых они не излучают и не поглощают энергии. В этих состояниях атомы обладают энергиями, образующими дискретный ряд Е₁, Е_2, Е_3, Е_4…

Атомы могут излучать или поглощать энергию лишь при переходе из одного стационарного состояния в другое, причем частоты излучения (поглощения) определяются правилом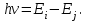

В стационарных состояниях электрон движется вокруг ядра по круговым орбитам, для которых момент импульса электрона принимает значения, кратные 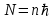: , n = 1, 2, 3, 4…

где h и =h/2 – постоянные Планка

3. Как образуются спектры с точки зрения теории Бора?

Имея в виду, что полная энергия атома как системы ядро – электрон связана с радиусом обращения электрона как E = –е²/2r, можно получить выражение для возможных значений энергий атома в стационарных состояниях: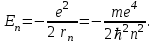



На рис. 3.2 графически изображены возможные значения энергии и соответствующие орбиты электронов в атоме водорода.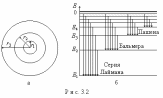


Основному (невозбужденному) состоянию при n = 1 соответствуют

= –13,6 эВ и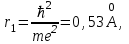

где r₁  так называемый первый боровский радиус.

При возбуждении атомы переходят в состояния c бóльшими значениями энергии и затем при обратных переходах, которые изображены стрелками и сгруппированы определенным образом на рис. 3.2, б, излучают, согласно правилу частот 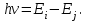серии линий

4. Покажите связь между формулой Бальмера и правилом частот Бора?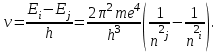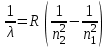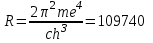

-> -> см^-1

5. Назовите основные аспекты развития теории атома водорода

Теория Бора верно отражала основные черты спектрального поведения атома водорода, однако не могла объяснить, например, тонкую структуру спектральных линий или их расщепление при помещении атома во внешнее поле. Следующий шаг в развитии теории атома был сделан А. Зоммерфельдом, который предположил, что электрон в атоме водорода может двигаться не только по круговым, но и по эллиптическим орбитам, для которых также должно выполняться условие квантования момента импульса

В развитие идей Бора Зоммерфельд распространил квантование на ориентации орбит электронов в атоме. Согласно идее «пространственного квантования», возможны лишь такие ориентации плоскости орбиты, при которых проекция момента импульса электрона на некоторое выделенное направление z принимает значения кратные 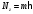, т. е. , где m – так называемое магнитное квантовое число, которое, может принимать значения, равные m = 0, 1, 2,…,  l.

Таким образом, состояние атома можно охарактеризовать тремя квантовыми числами n,l,m, которые определяют возможные траектории электрона и соответствующие физические величины Ε_n, N,N_z.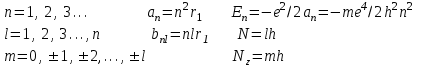



Следует отметить, что теория Бора–Зоммерфельда позволила не только качественно, но количественно, объяснить основные закономерности в атомных спектрах

6. Каковы основные недостатки теории атома Бора – Зоммерфельда?

• 
  Не смогла объяснить интенсивность спектральных линий.
  
• 
  Справедлива только для водородоподобных атомов и не работает для атомов, следующих за ним в таблице Менделеева без экспериментальных данных (энергии ионизации или других).
  
• 
  Теория Бора логически противоречива: не является ни классической, ни квантовой. В системе двух уравнений, лежащих в её основе, одно — уравнение движения электрона — классическое, другое — уравнение квантования орбит — квантовое.
  

Теория Бора являлась недостаточно последовательной и общей. Поэтому она в дальнейшем была заменена современной квантовой механикой, основанной на более общих и непротиворечивых исходных положениях. Сейчас известно, что постулаты Бора являются следствиями более общих квантовых законов. Но правила квантования широко используются и в наши дни как приближённые соотношения: их точность часто бывает очень высокой.

7. Какая взаимосвязь существует между квантовыми числами и каким образом они характеризуют возможные состояния атома водорода с квантовомеханической точки зрения?

Кратко рассмотрим конечный результат квантовомеханического описания атома водорода. Здесь состояние атома задается также тремя квантовыми числами: главным n, орбитальным lи магнитным m, которые принимают несколько иные значения, а именно:

n = 1, 2, 3,...; l = 0, 1, 2,..., n–1; m = 0, 1, 2, …, l.

С одной стороны, эти квантовые числа задают состояние электрона в виде так называемой волновой функции , квадрат модуля которой определяет вероятность dWтого, что частица будет обнаружена в пределах элементарного объема dV: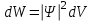



или, другими словами, 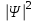дает плотность вероятности (вероятность, приходящуюся на единицу объема) нахождения частицы в данном месте пространства, т. е.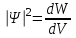

.

С другой стороны, квантовые числа n, l, m определяют некоторые физические величины, характеризующие состояния атома водорода. Так, возможные значения энергии атома определяется точно так же, как и в случае модели Бора – Зоммерфельда, а именно: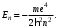



Момент импульса и его проекции определяются следующим образом: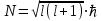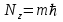



.

Чисто внешне приведенные результаты похожи на результаты теории Зоммерфельда.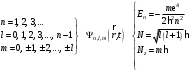



Однако результаты этих двух теорий имеют и существенные различия. Так, в квантовой теории нельзя говорить о траектории электрона; величину 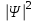весьма утрированно (и не совсем корректно) можно трактовать как распределение электрического заряда электрона около ядра; плотность такого электронного облака выше там, где величина 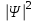имеет большее значение.

При квантовомеханическом рассмотрении атома водорода оказывается, что при различных значениях nквантовое число lможет принимать, в частности, нулевое значение, т. е. в состояниях с определенными, отличными от нуля, значениями энергии атома 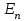величина момента импульса электрона может оказаться равной нулю (такие случаи соответствуют сферически симметричным волновым функциям). Кроме того, из сравнения выражений (3.9) и (3.10) следует, что при разрешенных взаимосвязях между квантовыми числами l и m величина проекции момента импульса N_z никогда не может достигать величины самого момента N. Эти и подобные им эффекты, согласующиеся с экспериментом, не имеют аналога в классической физике и поэтому называются квантовыми эффектами.

Ответы на контрольные вопросы по лабораторной работе №5
1. Перечислите стандартные условия, накладываемые на волновую функцию. Откуда эти условия возникают?

Поскольку волновая функция, с одной стороны, имеет вероятностный смысл, а, с другой – является решением уравне­ния Шредингера, т. е. дифференциального уравнения 2-го порядка, то на нее накладываются определенные, так называемые стандартные условия:

• 
  волновая функция 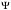должна быть конечна, непрерывна, однозначна;
  

• 
  производные 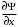, , 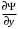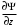должны быть непрерыв­ны;
  

• 
  волновая функция должна быть квадратично интегрируема, т. е. интеграл 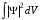должен быть конечным.
  

2. В чем состоит физический смысл распределения плотности в электронном облаке?

Кривая радиального распределения вероятности показывает, что электрон находится в тонком концентрическом шаровом слое радиуса r толщины dr вокруг ядра атома водорода.

Проекция максимума кривой соответствует боровскому радиусу α₀=0,53 Å.

3. Что определяет квадрат модуля волновой функции?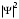

дает плотность вероятности (вероят­ность, отнесенную к единице объема) нахождения частицы в данном месте пространства, т. е.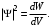



Интеграл взятый по всему пространству, должен быть равен единице: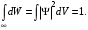



4. Что характеризуют квантовые числа: главное, орбитальное и магнитное? Какие значения они могут принимать?

Главное квантовое число (n) — целое число, для водорода и водородоподобных атомов определяет возможные значения энергии. В случаях сложных атомов нумерует уровни энергии с фиксированным значением азимутального (орбитального) квантового числа

Орбитальное (побочное или азимутальное) (l) квантовое число — в квантовой физике квантовое число ℓ, определяющее форму распределения амплитуды волновой функции электрона в атоме, то есть форму электронного облака.

Магни́тное ква́нтовое число́ (m) — квантовое число, параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы). Магнитное квантовое число характеризует ориентацию в пространстве орбитального момента импульса электрона или пространственное расположение атомной орбитали. {\displaystyle l}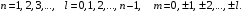



5. Какова кратность вырождения уровней энергии атома водорода?

Состояния с одинаковой энергией называются вырожденными, а число различных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня. Кратность вырождения уровней водорода легко вычислить, исходя из возможных значений для l и т.Каждому из пзначений квантового числа l соответствует 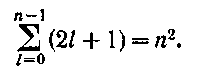значений квантового числа т. Следовательно, число различных состояний, соответствующих данному n, равно



Таким образом, каждый уровень энергии водородного атома имеет вырождение кратности п².

Однако это число можно удвоить из-за наличия спина электрона, то есть кратность вырождения будет равна 2n²

6. Каков квантовомеханический смысл первого боровского радиуса?

В основном состоянии атома водорода наиболее вероятным расстоянием от электрона до ядра является расстояние, равное боровскому радиусу. В этом заключается квантово-механический смысл боровского радиуса.

7. Каковы правила квантования орбитального механического и собственного механического моментов импульса электрона? Их проекций на направление внешнего магнитного поля?

Орбитальный момент импульса L электрона в атоме также может принимать лишь ряд дискретных значений L=(h/2π)√l(l+1), где l – орбитальное квантовое число

Проекция орбитального момента импульса L_z на выбранное направление OZ (например, направление внешнего магнитного поля) тоже квантуется L_z=(h/2π)m, где m – магнитное квантовое число

Собственный момент импульса (спин) электрона L_s также может принимать только ряд дискретных значений L_s=(h/2π)√s(s+1), где s – спиновое квантовое число

Проекция собственного момента импульса _Lsz на выбранное направление OZ (например, направление внешнего магнитного поля) тоже квантуется L_sz=(h/2π)m_s, где m_s – магнитное спиновое квантовое число

8. Почему атом водорода может иметь одну и ту же энергию, находясь в различных состояниях?

n – главное квантовое число,

l – орбитальное квантовое число,

m – магнитное квантовое число.

При данном n числа l и m могут принимать следующие значения:

l = 0, 1, 2, ..., n – 1 т. е. всего n различных значений;

m = – l,– l + 1, …–1, 0, +1, … , l – 1, l, т. е. всего 2l + 1 различных значений.

Таким образом, каждому Е_п(кроме Е₁)соответствует несколько волновых функций  , отличающихся значениями квантовых чисел l и m. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.