физика. 11 12 физика. Распределение Максвелла
 Скачать 0.5 Mb.
|
|
11 билет  Распределе́ние Ма́ксвелла — общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа. Вид соответствующей функции плотности вероятности диктуется тем, какая величина: скорость частицы, проекция скорости, модуль скорости, энергия, импульс и т. д. — выступает в качестве непрерывной случайной величины. В ряде случаев распределение Максвелла может быть выражено как дискретное распределение по множеству уровней энергии. Наиболее значимое распределение Максвелла записывается для модуля скорости частицы V в непрерывном случае и имеет плотность:  Распределение Максвелла лежит в основе кинетической теории газов, объясняющей многие фундаментальные свойства газов, включая давление и диффузию. С его помощью вычисляются средние и наиболее вероятные скорости и энергии молекул газа. Оно также применимо для описания электронных процессов переноса и других явлений в физике и химии. Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Данное распределение является реализующимся с наивысшей вероятностью распределением изучаемого параметра. Распределение Больцмана. 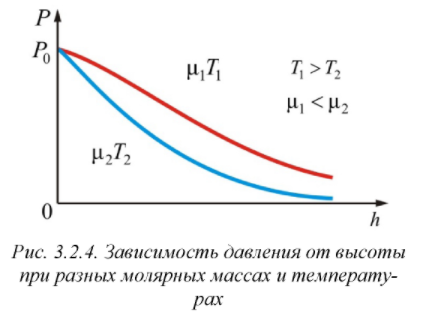   2) Ква́нтовая меха́ника — раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине с постоянной Планка. Предсказания квантовой механики могут существенно отличаться от предсказаний классической механики. Поскольку постоянная Планка является чрезвычайно малой величиной по сравнению с действием объектов при макроскопическом движении, квантовые эффекты в основном проявляются в микроскопических масштабах. Если физическое действие системы намного больше постоянной Планка, квантовая механика органически переходит в классическую механику. В свою очередь, квантовая механика является нерелятивистским приближением (то есть приближением малых энергий по сравнению с энергией покоя массивных частиц системы) квантовой теории поля. Квантовая теория родилась в 1901 г., когда Макс Планк предложил теоретический вывод о соотношении между температурой тела и испускаемым этим телом излучением, вывод, который долгое время ускользал от других ученых. Как и его предшественники, Планк предположил, что излучение испускают атомные осцилляторы, но при этом считал, что энергия осцилляторов (и, следовательно, испускаемого ими излучения) существует в виде небольших дискретных порций, которые Эйнштейн назвал квантами. Энергия каждого кванта пропорциональна частоте излучения. Хотя выведенная Планком формула вызвала всеобщее восхищение, принятые им допущения оставались непонятными некоторое время, так как противоречили классической физике. Е = h v где V - частота света, а h - универсальная постоянная, характеризующая меру дискретной порции энергии, которой обмениваются вещество и излучение. В атомную теорию вошли, таким образом, прерывистые физические величины, которые могут изменятся только скачками. Квантовая теория и теория относительности не относятся к классической физики. В 1900 г. немецкий физик Макс Планк предлагает Квантовую теорию излучения, согласно которой свет излучается не непрерывно (как это предполагается классической теорией), а дискретно — порциями, которые Планк назвал квантами. Несмотря на парадоксальность этой теории (в которой излучение света рассматривается, как непрерывный волновой процесс, и, в то же время, как поток частиц — квантов), она хорошо описывала форму непрерывного спектра теплового излучения твёрдых и жидких тел. В 1905 г. Альберт Эйнштейн предложил Специальную теорию относительности, в которой отвергается концепция абсолютности пространства и времени, и декларируется их относительность: величины пространственных и временных отрезков, относящихся к некоторому физическому объекту зависят от скорости движения объекта относительно выбранной системы отсчёта (системы координат). В разных системах координат эти величины могли принимать разные значения. В частности, одновременность независимых физических событий также была относительной: события происходившие одновременно в одной системе координат, в другой могли происходить в разные моменты времени. Эта теория позволяла построить логически непротиворечивую кинематическую картину мира без использования понятий ненаблюдаемых абсолютного пространства, абсолютного времени и эфира. ЗАДАЧА    12 билет 1) Распределения Больцмана и Максвелла позволяют определить соответственно зависимость концентрации молекул от координат  и функцию распределения по скоростям  . При этом распределение Больцмана описывается в пространстве координат  ,  и  , а распределение Максвелла в пространстве скоростей  ,  и  .Если ввести 6-мерное пространство, координатами молекулы в котором являются величины , , , ,  и , то функция распределения в таком пространстве будет зависеть от этих шести переменных:  . Считая пространственные переменные , ,  и компоненты скорости , , статистически независимыми друг от друга, на основании формулы можно записать:
или
где выражение для кинетической энергии имеет вид:
Первая формула описывает распределение, называющееся распределением Максвелла-Больцмана. Она может быть использована в случае, когда полная энергия молекулы  равна сумме её потенциальной энергий  во внешнем силовом поле и кинетической энергии  её поступательного движения:  .2) Диспе́рсия све́та (разложение света; светорассеяние]) — это совокупность явлений, обусловленных зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимостью фазовой скорости света в веществе от частоты (или длины волны). Экспериментально открыта Исааком Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее. Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является различие фазовых скоростей распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и, следовательно, цвета). Обычно, чем меньше длина световой волны, тем больше показатель преломления среды для неё и тем меньше фазовая скорость волны в среде. Электромагнитные волны способны распространяться не только в вакууме, но и в различных средах, т. е. в веществе. При этом претерпевает изменения и характеристики излучения, и характеристики вещества. Рассмотрим вкратце основанный' на представлениях классической физики механизм взаимодействия электромагнитной волны и вещества. Переменное поле волны действует на носители заряда в веществе (прежде всего на свободные электроны проводимости в металлических проводниках, электронные оболочки атомов, разноименные ионы, а также диполи в диэлектриках). При этом оказывается, что действие электрического поля в сотни раз сильнее, чем действие магнитного поля. Это позволяет в дальнейшем не принимать во внимание магнитные свойства вещества, для объяснения которых необходимо привлекать понятия квантовой механики, и рассматривать только электрические взаимодействия, т.е. , по сути, считать электромагнитную волну световым вектором. Поскольку электрическое поле световой волны периодическое, то микроскопические заряды вещества под действием волны совершают колебания. Энергия этих колебаний частично передастся другим частицам среды, в результате происходит поглощение излучения; вещество нагревается. С другой стороны колеблющиеся заряды, как и всякие ускоренные, излучают свои вторичные волны. Так осуществляется распространение электромагнитной волны. ЗАДАЧА При освещении фотокатода светом с длиной волны 400 нм, а затем 500 нм, обнаружили, что задерживающее напряжение для прекращения фотоэффекта изменилось в 2 раза. Определите работу выхода электронов из этого металла. Результат представьте в электрон – вольтах.   |
,
.
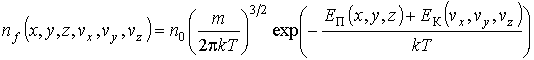