работы. 5 растяжения и сдвиги. Растяжения и сдвиги Задание 5 34

• Название: Растяжения и сдвиги Задание 5 34
• Анкор: работы
• Дата: 23.05.2022
• Размер: 0.57 Mb.
• Имя файла: 5 растяжения и сдвиги.docx
• Тип: Документы; #545594

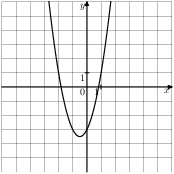
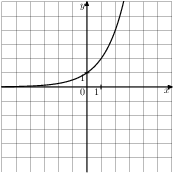
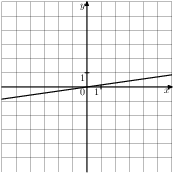
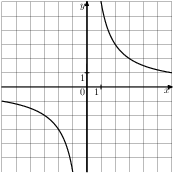
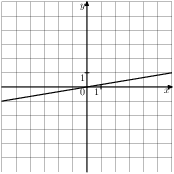
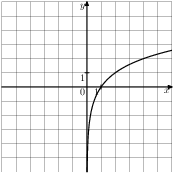
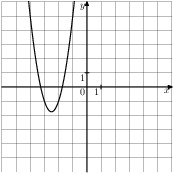
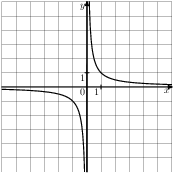
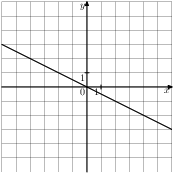
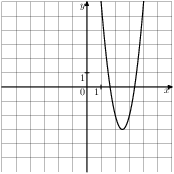
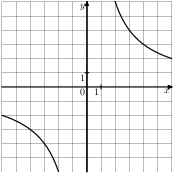
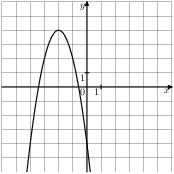
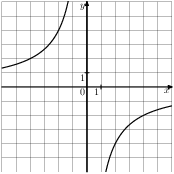
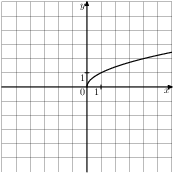
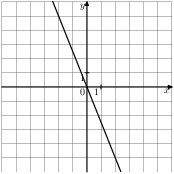
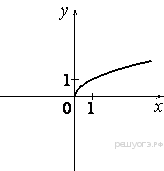
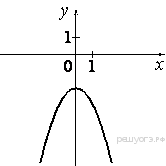
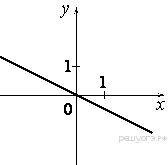
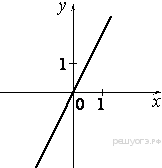
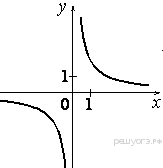
Рас­тя­же­ния и сдви­ги

1. За­да­ние 5 № 34. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют.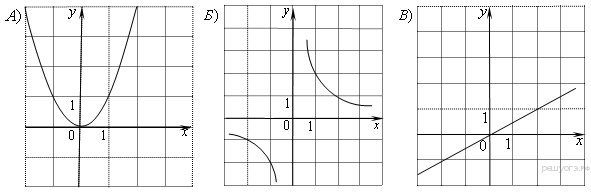



 1)  2)  3)  4) 

 Ответ ука­жи­те в виде по­сле­до­ва­тель­но­сти цифр без про­бе­лов и за­пя­тых в ука­зан­ном по­ряд­ке.

А	Б	В

 

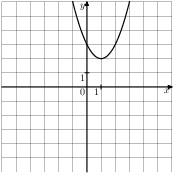
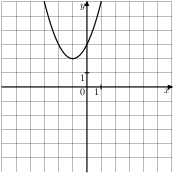
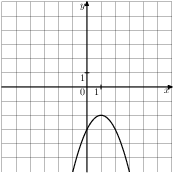
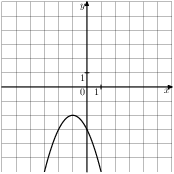
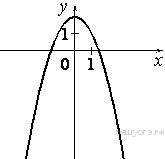
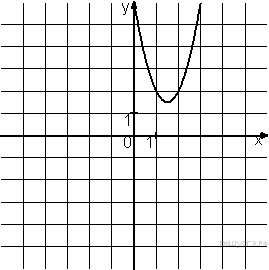
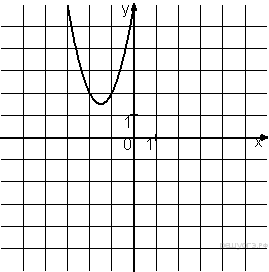
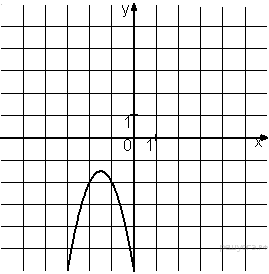
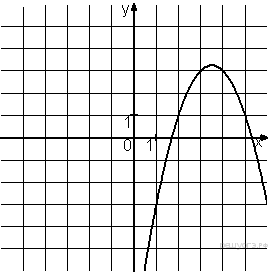
Ре­ше­ние. Опре­де­лим вид гра­фи­ка каж­дой из функ­ций.

1)   — урав­не­ние па­ра­бо­лы, ветви ко­то­рой на­прав­лен­ны вверх.

2)   — урав­не­ние пря­мой.

3)   — урав­не­ние верх­ней ветви па­ра­бо­лы, на­прав­лен­ной впра­во.

4)   — урав­не­ние ги­пер­бо­лы. Тем самым най­де­но со­от­вет­ствие: A — 1, Б — 4, В — 2. Ответ: 142.

2. За­да­ние 5 № 193087. Гра­фик какой из при­ве­ден­ных ниже функ­ций изоб­ра­жен на ри­сун­ке?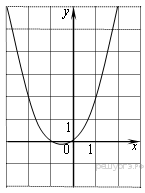

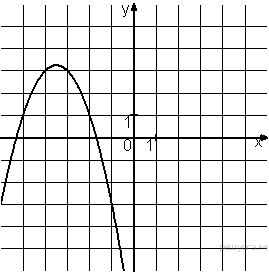
1)

2)

3)

4)

Ре­ше­ние. Ветви изоб­ражённой на ри­сун­ке па­ра­бо­лы на­прав­лен­ны вверх, а абс­цис­са вер­ши­ны от­ри­ца­тель­на. Сле­до­ва­тель­но, дан­но­му гра­фи­ку могут со­от­вет­сво­вать функ­ции   или  Вы­де­лим пол­ный квад­рат в обоих вы­ра­же­ни­ях:





Гра­фи­ку со­от­вет­ству­ет ва­ри­ант под но­ме­ром 3. Ответ: 3

3. За­да­ние 5 № 193093. На одном из ри­сун­ков изоб­ра­жен гра­фик функ­ции  . Ука­жи­те номер этого ри­сун­ка.

1)		2)
3)		4)

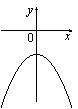
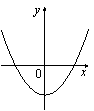
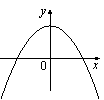
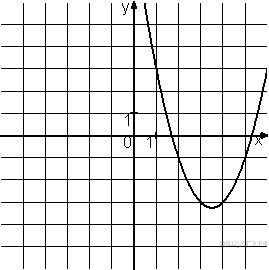
  Ре­ше­ние. Ко­эф­фи­ци­ент  , по­это­му ветви па­ра­бо­лы на­прав­ле­ны вверх. Абс­цис­са вер­ши­ны па­ра­бо­лы равна:  Пра­виль­ный ва­ри­ант от­ве­та ука­зан под но­ме­ром 1. Ответ: 1

4. За­да­ние 5 № 193097. На одном из ри­сун­ков изоб­ра­же­на па­ра­бо­ла. Ука­жи­те номер этого ри­сун­ка.

 

1)		2)
3)		4)

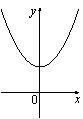
Ре­ше­ние. Па­ра­бо­ла изоб­ра­же­на на ри­сун­ке 1.Пра­виль­ный ответ ука­зан под но­ме­ром 1. Ответ: 1

5. За­да­ние 5 № 198175. Гра­фик какой из при­ве­ден­ных ниже функ­ций изоб­ра­жен на ри­сун­ке?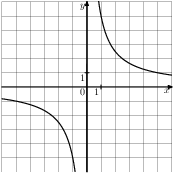

 

1)

2)

3)

4)

Ре­ше­ние. Изоб­ражённая на ри­сун­ке ги­пер­бо­ла рас­по­ло­же­на в пер­вой и тре­тьей чет­вер­тях, сле­до­ва­тель­но, дан­но­му гра­фи­ку могут со­от­вет­сво­вать функ­ции   или   При   ор­ди­на­та функ­ции на гра­фи­ке равна 5, сле­до­ва­тель­но, это гра­фик функ­ции  Ответ: 3.

6. За­да­ние 5 № 200515. На одном из ри­сун­ков изоб­ра­жен гра­фик функ­ции  . Ука­жи­те номер этого ри­сун­ка.

1)		2)
3)		4)

Ре­ше­ние.

Гра­фик функ­ции   — па­ра­бо­ла. Опре­де­лим тип каж­до­го гра­фи­ка функ­ции.

1) На пер­вом ри­сун­ке изоб­ра­же­на ли­ней­ная функ­ция.

2) На вто­ром ри­сун­ке изоб­ра­же­на ло­га­риф­ми­че­ская функ­ция.

3) На тре­тьем ри­сун­ке изоб­ра­же­на па­ра­бо­ла.

4) На четвёртом ри­сун­ке изоб­ра­же­на ги­пер­бо­ла. Ответ: 3.

7. За­да­ние 5 № 201145. На одном из ри­сун­ков изоб­ра­жен гра­фик функ­ции  . Ука­жи­те номер этого ри­сун­ка.

1)		2)
3)		4)

Ре­ше­ние.

Гра­фик функ­ции   — ги­пер­бо­ла. Опре­де­лим тип каж­до­го гра­фи­ка функ­ции.

1) На пер­вом ри­сун­ке изоб­ра­же­на ли­ней­ная функ­ция.

2) На вто­ром ри­сун­ке изоб­ра­же­на па­ра­бо­ла.

3) на тре­тьем ри­сун­ке изоб­ра­же­на по­ка­за­тель­ная функ­ция.

4) На четвёртом ри­сун­ке изоб­ра­же­на ги­пер­бо­ла.Ответ: 4.

8. За­да­ние 5 № 202195. На одном из ри­сун­ков изоб­ра­же­на ги­пер­бо­ла. Ука­жи­те номер этого ри­сун­ка.

1)		2)
3)		4)

Ре­ше­ние.

Ги­пер­бо­ла изоб­ра­же­на на ри­сун­ке 2.Ответ: 2.

9. За­да­ние 5 № 314771. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют. Гра­фи­ки

А)	Б)	В)

 Фор­му­лы

1)

2)

3)

4)

 За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В

Ре­ше­ние. Опре­де­лим вид гра­фи­ка каж­дой из функ­ций.

1)   — урав­не­ние пря­мой. 2)   — урав­не­ние ги­пер­бо­лы.

3)   — урав­не­ние па­ра­бо­лы, ветви ко­то­рой на­прав­лен­ны вниз.

4)   — урав­не­ние верх­ней ветви па­ра­бо­лы, на­прав­лен­ной впра­во.Ответ: 431.

10. За­да­ние 5 № 314772. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют. Гра­фи­ки

А)	Б)	В)

 Фор­му­лы

1)

2)

3)

4)

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В

Ре­ше­ние. Опре­де­лим вид гра­фи­ка каж­дой из функ­ций.

1)   — урав­не­ние ги­пер­бо­лы.

2)   — урав­не­ние па­ра­бо­лы, ветви ко­то­рой на­прав­лен­ны вверх.

3)   — урав­не­ние пря­мой.

4)   — урав­не­ние па­ра­бо­лы, ветви ко­то­рой на­прав­лен­ны вниз. Ответ: 314.

11. За­да­ние 5 № 316368. Уста­но­ви­те со­от­вет­ствие между функ­ци­я­ми и их гра­фи­ка­ми.

 ФУНК­ЦИИ

А)

Б)

В)

 ГРА­ФИ­КИ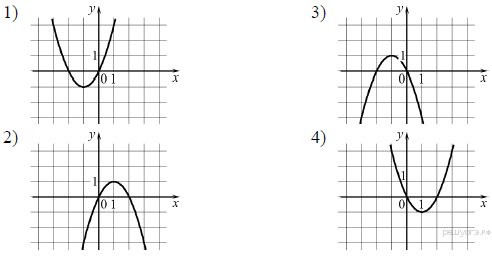



 За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В

Ре­ше­ние. На­пом­ним, что если па­ра­бо­ла за­да­на урав­не­ни­ем  , то: при   то ветви па­ра­бо­лы на­прав­ле­ны вверх, а при   — вниз; абс­цис­са вер­ши­ны па­ра­бо­лы вы­чис­ля­ет­ся по фор­му­ле   па­ра­бо­ла пе­ре­се­ка­ет ось Oy в точке с.

Урав­не­ние   за­да­ет па­ра­бо­лу, ветви ко­то­рой на­прав­ле­ны вверх, абс­цис­са вер­ши­ны равна  , она пе­ре­се­ка­ет ось ор­ди­нат в точке 0. Ее гра­фик изоб­ра­жен на ри­сун­ке 4).

Урав­не­ние   за­да­ет па­ра­бо­лу, ветви ко­то­рой на­прав­ле­ны вверх, абс­цис­са вер­ши­ны равна  , она пе­ре­се­ка­ет ось ор­ди­нат в точке 0. Ее гра­фик изоб­ра­жен на ри­сун­ке 1).

Урав­не­ние   за­да­ет па­ра­бо­лу, ветви ко­то­рой на­прав­ле­ны вниз, абс­цис­са вер­ши­ны равна  , она пе­ре­се­ка­ет ось ор­ди­нат в точке 0. Ее гра­фик изоб­ра­жен на ри­сун­ке 3).

Тем самым, ис­ко­мое со­от­вет­ствие: А—4, Б—1, В—3. Ответ: 413.

12. За­да­ние 5 № 321867. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = ax² + c. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми и зна­ка­ми ко­эф­фи­ци­ен­тов a и c.

 ГРА­ФИ­КИ

А)

Б)

В)

Г)

 ЗНАКИ КО­ЭФ­ФИ­ЦИ­ЕН­ТОВ

1) a > 0, c < 0

2) a < 0, c > 0

3) a > 0, c > 0

4) a < 0, c < 0

 За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В	Г

 Ре­ше­ние. Гра­фик функ­ции   — па­ра­бо­ла. Ветви этой па­ра­бо­лы на­прав­ле­ны вверх, если  и вниз, если   Зна­че­ние   опре­де­ля­ет ор­ди­на­ту вер­ши­ны па­ра­бо­лы. Если   то вер­ши­на па­ра­бо­лы на­хо­дит­ся над осью абс­цисс, а если мень­ше нуля, то ниже. Таким об­ра­зом, по­лу­ча­ем, ответ: A — 4, Б — 1, В — 2, Г — 3.Ответ: 4123.

13. За­да­ние 5 № 321919. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют.

А)

Б)

В)

 1)  2)  3)  4)   

Ответ ука­жи­те в виде по­сле­до­ва­тель­но­сти цифр без про­бе­лов и за­пя­тых в ука­зан­ном по­ряд­ке.

А	Б	В

 Ре­ше­ние. Вы­де­лим во всех вы­ра­же­ни­ях пол­ный квад­рат:

1)  Ветви па­ра­бо­лы на­прав­ле­ны вниз, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Та­ко­го гра­фи­ка среди име­ю­щих­ся — нет.

2)  Ветви па­ра­бо­лы на­прав­ле­ны вниз, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Такой гра­фик изоб­ражён на ри­сун­ке В).

3)  Ветви па­ра­бо­лы на­прав­ле­ны вверх, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Такой гра­фик изоб­ражён на ри­сун­ке Б).

4)  Ветви па­ра­бо­лы на­прав­ле­ны вверх, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Такой гра­фик изоб­ражён на ри­сун­ке А).Ответ: 432.

14. За­да­ние 5 № 321920. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют.

А)

Б)

В)

 

1)  2)  3)  4) 

 Ответ ука­жи­те в виде по­сле­до­ва­тель­но­сти цифр без про­бе­лов и за­пя­тых в ука­зан­ном по­ряд­ке.

А	Б	В

 Ре­ше­ние. Вы­де­лим во всех вы­ра­же­ни­ях пол­ный квад­рат:

1)   Ветви па­ра­бо­лы на­прав­ле­ны вверх, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Такой гра­фик изоб­ражён на ри­сун­ке Б).

2)  Ветви па­ра­бо­лы на­прав­ле­ны вниз, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Такой гра­фик изоб­ражён на ри­сун­ке В).

3)   Ветви па­ра­бо­лы на­прав­ле­ны вверх, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Та­ко­го гра­фи­ка нет среди пред­став­лен­ных.

4)  Ветви па­ра­бо­лы на­прав­ле­ны вниз, вер­ши­на па­ра­бо­лы на­хо­дит­ся в точке   Такой гра­фик изоб­ражён на ри­сун­ке А).

 Ответ: 412

15. За­да­ние 5 № 322008. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и фор­му­ла­ми, ко­то­рые их за­да­ют.

А)

Б)

В)

 1)  2)  3)  4) 

 Ответ ука­жи­те в виде по­сле­до­ва­тель­но­сти цифр без про­бе­лов и за­пя­тых в ука­зан­ном по­ряд­ке.

А	Б	В

  Ре­ше­ние.Все изоб­ражённые здесь гра­фи­ки — пря­мые. Урав­не­ние пря­мой: 

1) В пер­вом слу­чае пря­мая па­рал­лель­на оси абс­цисс, сле­до­ва­тель­но,   При этом 

2) Вто­рой гра­фик про­хо­дит через на­ча­ло ко­ор­ди­нат, зна­чит,   При уве­ли­че­нии   на еди­ни­цу, зна­че­ние   воз­рас­та­ет на две, сле­до­ва­тель­но, 

3) При   зна­чит,   ри уве­ли­че­нии   на еди­ни­цу, зна­че­ние   также воз­рас­та­ет на еди­ни­цу, сле­до­ва­тель­но,  Тем самым най­де­но со­от­вет­ствие: A — 4, Б — 1, В — 3. Ответ: 413

16. За­да­ние 5 № 339073. Уста­но­ви­те со­от­вет­ствие между функ­ци­я­ми и их гра­фи­ка­ми.

 Функ­ции

А)

Б)

В)

 Гра­фи­ки__Ре­ше­ние.'>Гра­фи­ки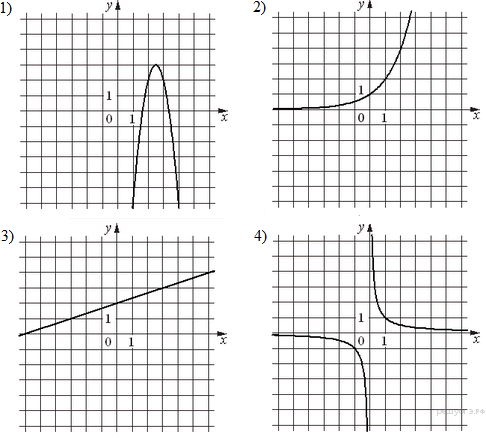

 

 За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В

Ре­ше­ние. Опре­де­лим вид гра­фи­ка для каж­дой из функ­ций.

А)   — ли­ней­ная функ­ция.

Б)   — па­ра­бо­ла.

В)   — ги­пер­бо­ла.

Таким об­ра­зом, ис­ко­мое со­от­вет­ствие: A — 3, Б — 1, В — 4. Ответ: 314.

17. За­да­ние 5 № 339091. Уста­но­ви­те со­от­вет­ствие между функ­ци­я­ми и их гра­фи­ка­ми.

 Функ­ции

А) y = −2x + 4

Б) y = 2x − 4

В) y= 2x + 4

 Гра­фи­ки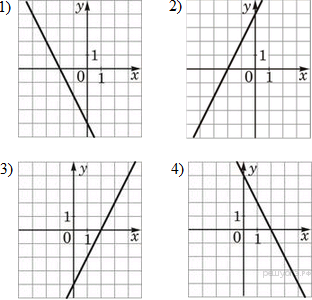

 

 За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В

Ре­ше­ние. Если пря­мая за­да­на урав­не­ни­ем   то при  функ­ция воз­рас­та­ет, при   — убы­ва­ет. Зна­че­нию   со­от­вет­сву­ет зна­че­ние функ­ции в точке 

Урав­не­ние   задаёт убы­ва­ю­щую функ­цию, пе­ре­се­ка­ю­щую ось ор­ди­нат в точке 4.

Урав­не­ние   задаёт воз­рас­та­ю­щую функ­цию, пе­ре­се­ка­ю­щую ось ор­ди­нат в точке −4.

Урав­не­ние   задаёт воз­рас­та­ю­щую функ­цию, пе­ре­се­ка­ю­щую ось ор­ди­нат в точке 4.

 Тем самым, ис­ко­мое со­от­вет­ствие: А — 4, Б — 3, В — 2. 

Ответ: 432.

18. За­да­ние 5 № 339114. Уста­но­ви­те со­от­вет­ствие между функ­ци­я­ми и их гра­фи­ка­ми.

Функ­ции  А)

Б)

В)

 Гра­фи­ки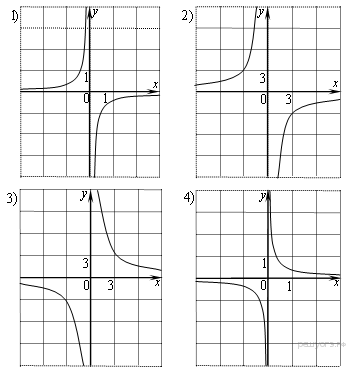

 

Ре­ше­ние. Все пред­став­лен­ные здесь функ­ции — ги­пер­бо­лы. Общая фор­му­ла для урав­не­ния ги­пер­бо­лы:  , если  , то ветви ги­пер­бо­лы рас­по­ла­га­ют­ся в пер­вой и тре­тьей чет­вер­тях, в про­тив­ном слу­чае — во вто­рой и четвёртой чет­вер­тях.

Для того, чтобы от­ли­чить ги­пер­бо­лы ле­жа­щие в оди­на­ко­вых чет­вер­тях нужно под­ста­вить какое-ни­будь зна­че­ние   в фор­му­лу и про­ве­рить, ка­ко­му гра­фи­ку будет со­от­вет­ство­вать по­лу­чен­ное зна­че­ние.

Таким об­ра­зом, уста­но­вим со­от­вет­ствие: А — 4, Б — 3, В — 2. Ответ: 432.
19. За­да­ние 5 № 339254. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = ax² + bx + c. Уста­но­ви­те со­от­вет­ствие между зна­ка­ми ко­эф­фи­ци­ен­тов a и c и гра­фи­ка­ми функ­ций.

 Ко­эф­фи­ци­ен­ты

А) a > 0, c < 0

Б) a < 0, c > 0

В) a > 0, c > 0

 Гра­фи­ки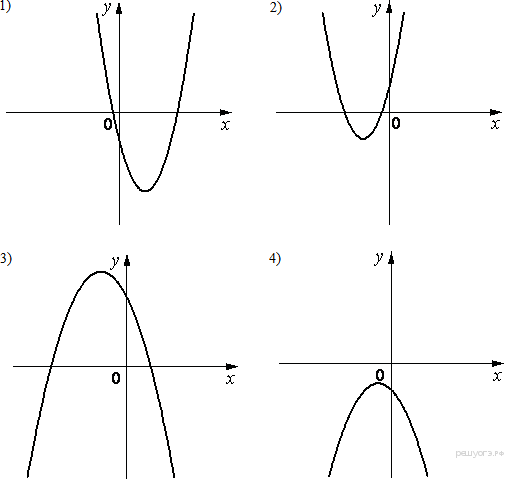

 

 За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В

Ре­ше­ние. Если па­ра­бо­ла за­да­на урав­не­ни­ем  , то: при   то ветви па­ра­бо­лы на­прав­ле­ны вверх, а при   — вниз. Зна­че­ние c со­от­вет­ству­ет зна­че­нию функ­ции в точке x = 0. Сле­до­ва­тель­но, если гра­фик пе­ре­се­ка­ет ось ор­ди­нат выше оси абс­цисс, то зна­че­ние c по­ло­жи­тель­но, если ниже оси абс­цисс — от­ри­ца­тель­но.  Таким об­ра­зом, функ­ци­ям со­от­вет­ству­ют сле­ду­ю­щие гра­фи­ки: А  1, Б  3, В 2. Ответ: 132.

20. За­да­ние 5 № 341325. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = kx + b. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и зна­ка­ми ко­эф­фи­ци­ен­тов k и b.

Гра­фи­ки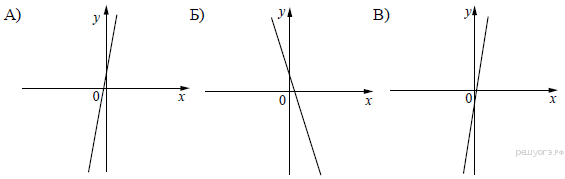

 

 Ко­эф­фи­ци­ен­ты

1) k < 0, b > 0

2) k > 0, b > 0

3) k < 0, b < 0

4) k > 0, b < 0

 За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам: 

А	Б	В

Ре­ше­ние. Если пря­мая за­да­на урав­не­ни­ем   то при   функ­ция воз­рас­та­ет, при   — убы­ва­ет. Зна­че­нию   со­от­вет­сву­ет зна­че­ние функ­ции в точке   Таким об­ра­зом, гра­фи­ку A со­от­вет­ству­ют ко­эфи­ци­ен­ты 2, Б − 1, В − 4. Ответ: 214.