|
|
опорный конспект Виды прямолинейного движения. конспект виды движения. Равномерное неравномерное
 
Виды движения: прямолинейное
равномерное
|
неравномерное
|
Движение, при котором тело за любые равные промежутки времени совершает одинаковое перемещение
|
Движение, при котором тело за любые равные промежутки времени совершает не одинаковое перемещение
|
Скорость равномерного прямолинейного движения – это физическая величина, численно равная изменению координаты тела за единицу времени
При равномерном движении скорость постоянна. ( ускорение а равно 0)
Обозначение : ϑ
Единица измерения в СИ : м / с
Перевод из км/ч в м/с
Х км/ ч = 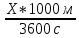
18 км/ ч = 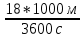 = 5 м / с = 5 м / с
S = ϑ t x = x0 + ϑ t
Графики зависимости от времени
|
Средняя скорость неравномерного движения равна отношению всего пройденного пути ко всему затраченному времени ϑ ср. = 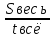
|
Равнопеременное движение – движение при котором тело изменяет свою скорость на одну и ту же величину.
|
Равноускоренное ( тело разгоняется - ускорение положительное ( 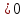 ) ) ) )
Ускорение – физическая величина, показывающая быстроту изменения скорости. Ускорение постоянно (для каждого вида движения)
|
Равнозамедленное ( тело тормозит -ускорение отрицательное ( 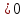 ) ) ) )
Ускорение численно равно изменению скорости за единицу времени
a = 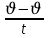 0 0
|
В формулах для расчёта скорости, перемещения, координат и ускорения
при разгоне перед ускорением а стоит знак « + плюс »
|
В формулах для расчёта скорости, перемещения, координат и ускорения
при торможении перед ускорением а стоит знак « - минус »
|
  координаты координаты
 х х
0 t
|
Перемещения
  S S
 0 t 0 t
|
Скорости


 0 t 0 t
|
Формулы: Скорости ϑ = ϑ0 + аt
Перемещения S = ϑ0 t + 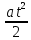
 S =( ϑ2 - ϑ0 2 )/2 а S =( ϑ2 - ϑ0 2 )/2 а
Координаты X = X0 + ϑ0 t + 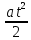
|
Графики
скорости
|
Перемещения, координат
|
ускорения
|
  a a

 0 t 0 t
|
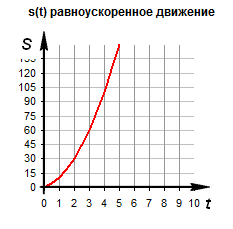
|
 a a
а 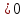

 0 t 0 t
|
1.Найти среднюю скорость движения автобуса, если первую половину пути он проехал за 3 минуты, а вторую половину пути проехал за 2 минуты. Весь путь составляет 5 км.
|
2.Найти скорость и перемещение тела через 4 с.Тело двигалось без начальной скорости с ускорением 2
м/ с
|
3.От станции А выехал поезд со скоростью 54 км/ч, навстречу ему движется поезд со скоростью 72 км/ч. Расстояние между станциями 33,6 км. Определить время, через которое поезда встретятся и место встречи.
|
  Дано: С И Решение Дано: С И Решение
S1 = 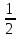 S ϑ ср = S ϑ ср = 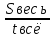
S2 = 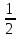 S Sвесь = S1 + S2 = S S Sвесь = S1 + S2 = S
t1 = 3 180 с t всё = t1 + t2
t2 = 2 120 с ϑ ср = 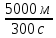 = 16,7 м/с = 16,7 м/с
S = 5 км 5000 м
 ϑ ср -? Ответ: 16,7 м/ с ϑ ср -? Ответ: 16,7 м/ с
|
  Дано: СИ Решение Дано: СИ Решение
ϑ0 = 0 ϑ = ϑ0 + аt
t = 4 c S = ϑ0 t + 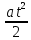
a = 2 м/c2 ϑ = 0 + (2 м/ с2 4с)
 S = ? м ϑ = 8м/с S = ? м ϑ = 8м/с
ϑ = ? м/с S = 16 м
|
Дано: СИ
 ϑ1 =54 км/ч 15 м/с ϑ1 =54 км/ч 15 м/с
ϑ2 = 72 км/ч 20 м/с
 S = 33,6 км 33600 м S = 33,6 км 33600 м
Х ? м
t-? с
|
В формулах , чтобы учитывать направление , записывают проекции величин на ось.
 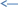
  ϑ1 ϑ2 ϑ1 ϑ2
  Х Х
Ось Х
ϑ1х = ϑ1
ϑ2х = - ϑ2
|
 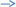 
 ϑ1 ϑ2 ϑ1 ϑ2
Х01 33600 м Х02
|
Решение: место встречи – одинаковая координата, значит запишем уравнение координат ( формулу) для обоих поездов:
Х 1 = Х01 + ϑ01 t 1
Х 2 = Х0 2 + ϑ02 t2
скорость постоянная, поэтому её можно обозначить как ϑ0 или ϑ, движение равномерное, значит ускорение а = 0
Х1 = Х2 , Х01 =0, Х02 = S
время движения одинаково, т.е.
t1 = t2 . ϑ01 t = S - ϑ02 t
t (ϑ01 + ϑ02 ) = S
Выразим t , найдём Х1
t= 960 с, Х1 = 14,4 км
| |
|
|
 Скачать 65.68 Kb.
Скачать 65.68 Kb.
