Разработка программы расчета значений функций, решения нелинейного уравнения и вычисления интеграла

• Название: Разработка программы расчета значений функций, решения нелинейного уравнения и вычисления интеграла
• Дата: 19.11.2020
• Размер: 0.84 Mb.
• Имя файла: Otchyot_RGR_Alsu_ispravlenny.docx
• Тип: Пояснительная записка; #151794
• страница: 2 из 3

Оглавление

Задание к расчетно-графической работе 2

Математическая формулировка задачи 3

Общая схема алгоритмов 6

Текст программы 13

Таблица значений функций 27

Графики функций 28

Интерфейс программы 29

Список используемой литературы 34

Задание к расчетно-графической работе

1. 
   Реализовать анимированную заставку.
   
2. 
   Разработать схему алгоритма, написать и отладить программу для расчёта и построения графиков двух функций (результаты расчётов должны храниться в виде массивов и распечатываться в виде таблицы) необходимо выделить наибольшее и наименьшее значения для каждой функций.
   

Исходные данные: a=2, b=4, n=16,

F1= ,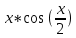

F2=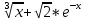

3.Разработать программу нахождения корней уравнения f(x) = 0 на интервале [a,b] с точностью е = 0.001 (интервал подобрать или рассчитать самостоятельно). При реализации можно использовать метод половинного деления (бисекции) или метод хорд: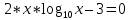



4.Разработать программу для вычисления значения определённого интеграла на интервале [a,b] (a,b подобрать самостоятельно) численными методами прямоугольников и трапеций для следующего варианта: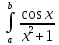

Математическая формулировка задачи

Для нахождения данных функции заданная область их определения, равномерно делится на 12 частей (n=12). Длина полученных интервалов (шаг) находится по формуле 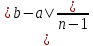. Затем вычисляются значения в каждой точке, которые в цикле подставляются в функции. Результаты выводятся в виде таблицы. Далее находятся минимальные и максимальные значения функций. Вычисления производятся для функций

F1= ,,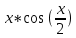

F2= .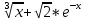

Пусть задано 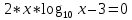и интервал (a,b). Алгоритм нахождения корня на интервале методом половинного деления сводится к следующей последовательности действий:

1) вычисляется середина интервала с=(a+b)/2;

2) если |f(c)|-5 определяет погрешность вычислений, то c будет являться приближенным значением корня уравнения и выводится как результат расчетов;

3) если |f(c)|>e, то проверяются знаки функций f(a) и f(c) на концах отрезка (a,c), для чего вычисляется их произведение. Если f(a)*f(c)<0, то функции будут иметь противоположные знаки и корень находится на отрезке (a,c). В этом случае интервал (a,b) заменяется отрезком (a,c), для чего присвоим b=c;

4) иначе, если f(a)*f(c)>0, корень уравнения находится на отрезке (c,b) и в расчетах интервал (a,b) заменяется (c,b), для чего присвоим a=c;

5) вычисления по схеме п.1-п. 4 повторяются в итерационном цикле до тех пор, пока не выполнится условие п. 2 - |f(c)|< e.

В случае метода хорд схема алгоритма расчета корня уравнения остается прежней за исключением п.1, в котором используется формула с = (a f(b) – b f(a))/(f(b) – f(a)).
Приближенное значение определенного интеграла вычисляется как сумма площадей N прямоугольников, построенных на интервале интегрирования (a,b). Интервал (a,b) разбивается на N равных частей длиной h = (b-a)/N, на каждой из которых строится прямоугольник с высотой, равной значению функции f(x_i) в центре участка с координатой x_i = a+(i-0.5)h, где i =1,2,...,N

Формула прямоугольников для приближенного вычисления значения интеграла имеет вид: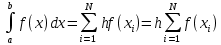



В методе трапеций интервал (a,b) разбивается на N равных частей длиной h = (b–a)/N, на каждой из которых строится трапеция. Приближенное значение интеграла определяется суммой площадей трапеций, построенных на интервале (a,b):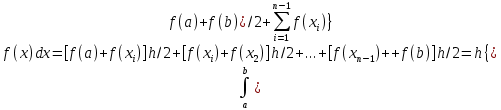

, где x_i =a+i* h.

Общая схема алгоритмов

Расчетно-графическая работа содержит:

1. 
   Сведения об авторе
   
2. 
   Вычисление значений двух функций с выводом результатов на экран в виде таблицы и выделением минимальных и максимальных значений;
   
3. 
   Построение графиков этих функций;
   
4. 
   Вычисление определенного интеграла;
   
5. 
   Решение нелинейного уравнения;
   
6. 
   Анимированную заставку;
   

Для выполнения этих задач было разработано меню, в котором управление осуществляется путем нажатия стрелок на клавиатуре. Общая схема меню представлена на рисунке 1. На рисунках 2.1 и 2.2 представлена детальная схема алгоритма табулирования функции. На рис. 3 детальный алгоритм построения графика функций. На рисунке 5 алгоритм решения интеграла методами прямоугольника и трапеции. На рисунке 4 алгоритм решения уравнений методами половинного деления и хорд .


Начало





While=folse



true



2

Управление стрелками



Menu





about


1


first
2


second
3




third
4




grafiki


5


anime
6


exit

2


7


1

Рисунок 1 Схема алгоритма реализации меню



first начало



z[16],

r[16],

k[16],

zmin=0,

rmin=0,

zmax=0,

rmax=0

b=4,

a=2, n=16,



r[i] =pow(k[i],1/3)+sqrt(2)*pow(exp(k[i]),-k[i])

zmin = z[0], zmaz=z[0],

rmin = r[0], rmax=r[0]

Рисунок 2.1 Схема алгоритма табулирования функции

i=0;i
1

k[i+1]=k[i]+dx

да

нет

нет

да

rmin = r[i]; 

rmax = r[i]; 

r[i] < rmin

r[i] > rmax

нет

zmin = z[i]; 

да

z[i] < zmin

нет

zmax=z[i]; 

z[i] > zmax

да

z[i] = k[i]*cos(k[i]/2)

k[0]=a;

dx=fabs(b-a)/(n-1)



1

Конец

first

Рисунок 2.2 Схема алгоритма табулирования функции

Вывод

zmin,rmin,zmax,rmax

k[i+1]=k[i]+dx

нет

нет

да

да

Вывод r[i]

Вывод a2[n]

Вывод r[i]

Выбор красного цвета

r[i]=rmin

Выбор зеленого цвета

r[i]=rmax

n=0,133

Вывод r[i]

Вывод z[i]

Вывод z[i]

нет

нет

да

Выбор красного цвета

z[i]=zmin

да

Выбор зеленого цвета

z[i]=zmax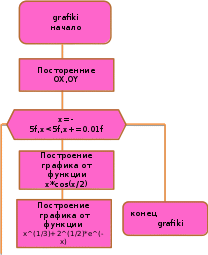







Рисунок 3 Схема алгоритма построения графиков





Рисунок 4 Решения уравнений методами половинного деления и хорд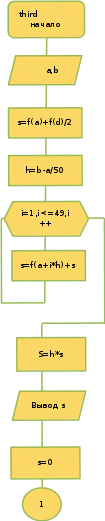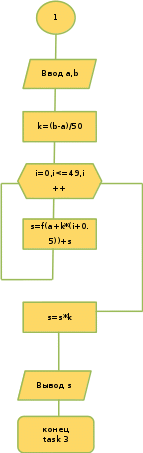



Рисунок 5 Схема алгоритма решение интегралов