урок по математике. Тюжин Аркадий. Разработка урока алгебры в 9 классе по теме Решение неравенств второй степени с одной переменной

• Название: Разработка урока алгебры в 9 классе по теме Решение неравенств второй степени с одной переменной
• Анкор: урок по математике
• Дата: 21.11.2022
• Размер: 78.52 Kb.
• Имя файла: Тюжин Аркадий.docx
• Тип: Разработка урока; #802749

Разработка урока алгебры
в 9 классе по теме
«Решение неравенств второй

степени с одной переменной»

(






ax² + bx + c > 0

Выполнил: Тюжин Аркадий ученик 9 класса

Данный урок является уроком систематизации знаний. К этому уроку обучающиеся обладают знаниями решения неравенств второй степени с одной переменной, но у них нет прочно сформированного навыка.
Цель: сформировать навык решения неравенств второй степени с одной переменной.
Задачи:

1) развивающая: развивать логическое мышление путем нахождения соответствий между ответами и символами;

2) образовательная: закрепить применение алгоритма решения неравенств второй степени с одной переменной при решении заданий;
Ход урока:

1. 
   Организационный момент. Здравствуйте.
   

Ребята, познакомившись на прошлом уроке с решением неравенств второй степени с одной переменной, как выдумаете, чем мы займемся сегодня? (Предполагаемый ответ: продолжим решать такие неравенства.) Все верно. Цель нашего урока – сформировать навык решения подобных неравенств.


1




2




3




4




М




5




6




7

1. 
   Степень квадратичной функции (вторая)
   
2. 
   Зависимость, при которой каждому значению икса соответствует единственное значение игрека (функция)
   
3. 
   Части параболы, симметричные друг другу относительно оси симметрии (ветви)
   
4. 
   Линия, являющаяся графиком квадратичной функции (парабола)
   
5. 
   Точка, из которой исходят ветви параболы (вершина)
   
6. 
   Результат решения уравнения (корень)
   
7. 
   Какое максимальное количество корней может иметь уравнение a 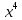+ bx³ + cx² + dx = 0 (четыре)
   

2. 
   Устная работа.
   

Решив ряд уравнений и неравенств, и найдя соответствие ответов


x² - 4 = 0 (корни 2 и -2)

2x - x² = 0 (корни 0 и 2)

x² + 10x + 25 = 0 (корень 5)

(x – 5) (x + 1) = 0 (корни 5 и -1)

x² - 3x + 2 = 0 (корни 2 и 1)

x² - 4 >0 (- ∞; - 2) U ( 2; + ∞)

(x – 3) (x – 4) < 0 (3; 4)

(x – 5) (x + 1) >0 (- ∞; - 1) U (5; +∞)

3. 
   Закрепление темы (работа у доски).
   

Решим несколько неравенств. Используя найденные множества решений и данные таблицы (см. приложение №1)

А

В 3412
x² - 10x – 24 > 0 x² - 7x + 10 < 0

4. 
   Музыкальная физминутка. (Ученики под руководством учителя делают упражнения)
   

5. 
   Закрепление материала (продолжение)
   

В 3412

C 3412



5x² - 9x - 2> 0 - x² + x + 30 < 0


D 3412

E 3412



14x² - 49x + 42 ≥ 0 x² - 6x < 4x - 25


(За работу у доски ученикам выставляется отметка.

6. 
   Итог урока.
   

Завершая урок, я попрошу вас ответить на следующие вопросы:

- какова была цель урока?

- что нового вы узнали на уроке?

- что вам понравилось на уроке?

- достигли ли мы цели урока?
7. Домашняя работа.

Откройте дневники и запишите домашнее задание:

параграф ____; №____, № ____.