Дипломная работа. Разработка виртуального лабораторного комплекса по дисциплине Методы оптимизации
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
4. РАЗРАБОТКА АЛГОРИТМОВВесь лабораторный комплекс при его проектировании и разработке можно разделить на три основных модуля, которые необходимо реализовать: модуль регистрации/авторизации, основной модуль обработки функции и модуль тестирования. Разработка каждого из них будет описана далее. 4.1. Модуль регистрации/авторизацииЧтобы ввести в виртуальный комплекс систему индивидуального оценивания прохождения студентом лабораторной работы, этого студента необходимо каким-либо образом идентифицировать. Самый простой способ сделать это – обеспечить разрабатываемому приложению поддержку функций регистрации/авторизации пользователя. Для хранения данных обо всех студентах и в дальнейшем их результатов выполнения лабораторных работ, создаётся база данных. Для этого используется интегрированная в среду разработки Visual Studio технология Entity Framework, поддерживающая базы данных MySQL. При создании базы данных используется так называемый «Model First» подход, при котором сперва строится модель базы данных (Рисунок 11), а уже по ней автоматически генерируется программный код. Так как в системе должны храниться лишь основные сведения о студентах и результаты их лабораторных работ, в базе будут содержаться минимальные данные: ФИО студента, уникальный логин, пароль, № группы, а также баллы за каждую из 4-ёх включенных в программу лабораторных работ. 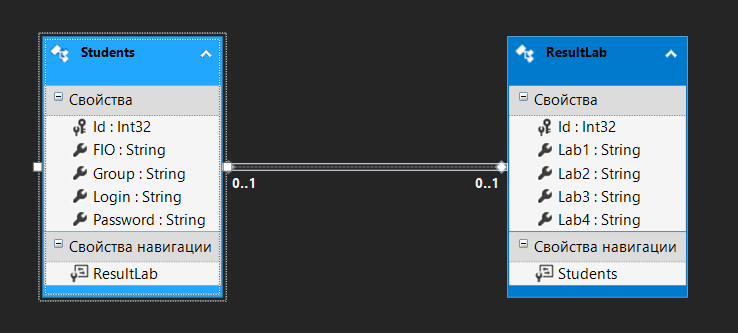 Рисунок 11 – Модель базы данных Прежде всего генерируются отдельные публичные классы Students.cs (студенты) (Рисунок 12), каждый экземпляр которого обладает четырьмя свойствами (выше перечисленные данные), и ResultLab.cs (результаты лабораторных работ) (Рисунок 13), где свойствами каждого экземпляра являются номера лабораторных работ с первой по четвертую. 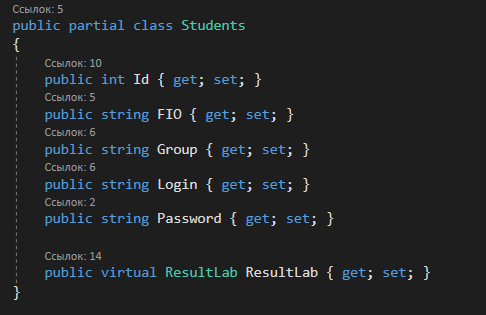 Рисунок 12. Класс «студенты» 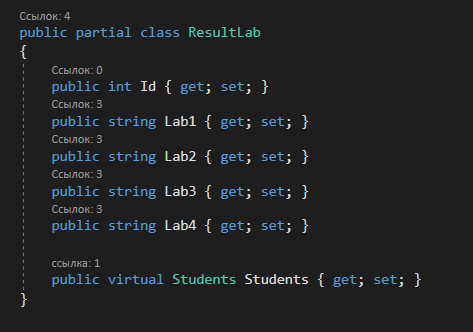 Рисунок 13 - Класс «Лабораторные работы» Связь в базе данных между двумя этими сущностями осуществляется посредством введения характеристики – idстудента, являющегося уникальным. Для обращения к базе данных используются запросы на языке SQL. Так, например, для добавления нового студента при его первом входе в комплекс и выборе функции регистрации используется следующая конструкция запроса: Students students = new Students() { FIO = txtbFIO.Text, Group = txtbGroup.Text, Login = txtbLog.Text, Password = txtbPass.Text }; db.StudentsSet.Add(students); db.SaveChanges(); В первой строке мы создаём новый экземпляр класса Students, которому присваиваем характеристики, введенные пользователем в текстовые поля формы. Затем мы добавляем данные нового студента в базу данных и сохраняем изменения. При авторизации студента программой проверяется наличие введенного им в базе данных логина и соответствия этому логину введенного пароля. В случае возникновения ошибок в ходе этих проверок программа требует ввести данные корректно, либо зарегистрировать студента с новым логином. В случае успешной регистрации или авторизации программа осуществляет переход к главной части комплекса – выбору лабораторной работы и соответственно к следующему модулю – обработки функции и алгоритмов методов оптимизации. В данный модуль также входит функция авторизации в системе преподавателя. Она осуществляется при введении преподавателем программно обозначенного кода, который даёт доступ к окну успеваемости студентов, что является частью уже другого модуля – модуля тестирования. 4.2. Модуль обработки функцииПосле выбора лабораторной работы программа переходит непосредственно к работе с алгоритмом, соответствующим выбранной теме. Программа на этом этапе должна обработать введенную студентом функцию и начальные данные, произвести над ними вычисления согласно определенному методу оптимизации и выдать результат в виде значений минимальной точки функции в заданном отрезке и значения этой функции в данной минимальной точке. За этап самой логической обработки и представления введенной пользователем функции в доступном программе виде отвечает алгоритм преобразования обратной польской записи, а за исполняемые на следующем для программы шаге вычисления алгоритмы методов оптимизации. Далее реализация каждой из этих двух частей рассматривается подробнее. 4.2.1. Обратная польская записьТак как вводимая пользователем в текстовое поле функция является для программы всего лишь строкой, то есть переменной типа string, возникает необходимость преобразовать эту строку таким образом, чтобы над ней можно было производить дальнейшие вычисления согласно алгоритму метода оптимизации. Чаще всего для таких преобразований используется обратная польская запись, или сокращенно ОПЗ. Обратная польская запись (англ. Reverse Polish notation, RPN) — форма записи математических и логических выражений, в которой операнды расположены перед знаками операций. Отличительной особенностью обратной польской нотации является то, что все аргументы (или операнды) расположены перед знаком операции. В общем виде запись выглядит следующим образом: Запись набора операций состоит из последовательности операндов и знаков операций. Операнды в выражении при письменной записи разделяются пробелами. Выражение читается слева направо. Когда в выражении встречается знак операции, выполняется соответствующая операция над двумя последними встретившимися перед ним операндами в порядке их записи. Результат операции заменяет в выражении последовательность её операндов и её знак, после чего выражение вычисляется дальше по тому же правилу. Результатом вычисления выражения становится результат последней вычисленной операции. Существует два наиболее известных способа преобразования в ОПЗ: Преобразование выражения в ОПЗ с использованием стека; Преобразование выражения в ОПЗ с помощью рекурсивного спуска. Во втором случае реализация алгоритма представляет собой несколько функций, последовательно вызывающих друг друга. Для программной реализации больше подходит первый способ. Алгоритм обработки польской записи следующий: Рассматриваем поочередно каждый символ. Если этот символ - число (или переменная), то поместить его в выходную строку. Если символ - знак операции, то проверить приоритет данной операции. Операции умножения и деления имеют наивысший приоритет. Операции сложения и вычитания имеют меньший приоритет. Наименьший приоритет имеет открывающая скобка. Получив один из этих символов, нужно проверить стек: Если стек все еще пуст, или находящиеся в нем символы (а находится в нем могут только знаки операций и открывающая скобка) имеют меньший приоритет, чем приоритет текущего символа, то поместить текущий символ в стек. Если символ, находящийся на вершине стека имеет приоритет, больший или равный приоритету текущего символа, то извлечь символы из стека в выходную строку до тех пор, пока выполняется это условие; затем перейти к пункту а). Если текущий символ - открывающая скобка, то поместить ее в стек. Если текущий символ - закрывающая скобка, то извлечь символы из стека в выходную строку до тех пор, пока не встретится в стеке открывающая скобка (т.е. символ с приоритетом, равным 1), которую следует просто уничтожить. Закрывающая скобка также уничтожается. Если вся входная строка разобрана, а в стеке еще остаются знаки операций, извлекаем их из стека в выходную строку. Для реализации данного алгоритма необходимо для начала создать несколько классов: operators.cs (Рисунок 14); OperatorContainer (Рисунок 15). Класс operatorsимеет публичный доступ – нужен для того, чтобы проверять и записывать у каждого оператора (знака операции) само значение знака и его приоритет. 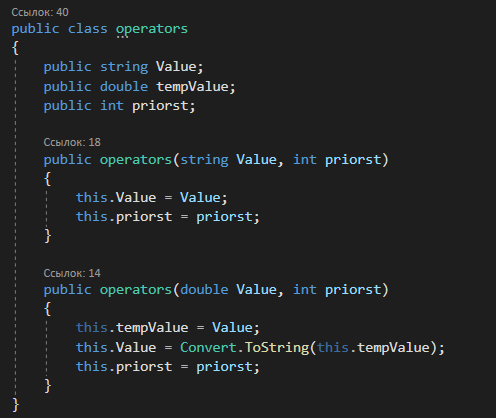 Рисунок 14 – Класс «Операторы» Класс OperatorContainer также имеет публичный доступ – это класс который содержит все возможные знаки операций и их приоритеты, и метод Find(), который позволяет найти знак, то есть сравнить текущий символ читаемой строки со списком операторов и найти нужный. 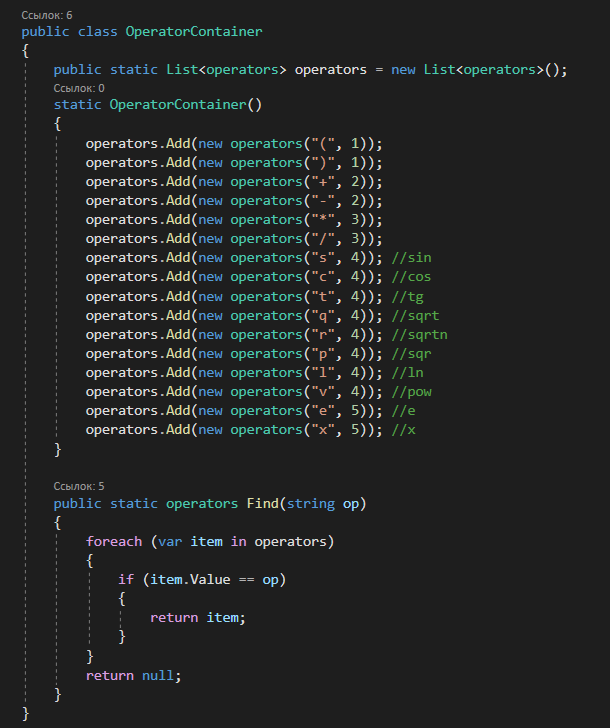 Рисунок 15 – Класс «контейнер операторов» Преобразование обратной польской записью происходит в функции Calculation (function.cs). Обработка строки происходит в цикле for, в котором выполняются следующие шаги: определяется, чем является символ: знаком операции или переменной; если это переменная, то она добавляется в выходную строку; если это знак операции, то определяется его приоритет и согласно алгоритму обратной польской записи, размещается либо в стек, либо в выходную строку вместе с другими знаками операции, уже хранившимися в стеке; стек опустошается до конца, если в нем что-то остается, когда все выражение функции обработано. Для обозначения операций используются следующие специальные обозначения, которые потом преобразуются в логические операции, доступные для выполнения программой: 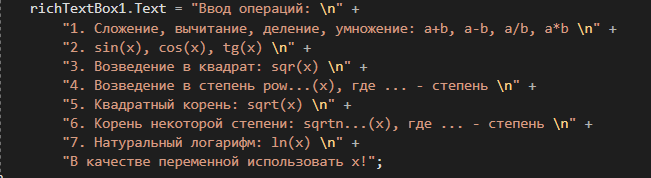 Рисунок 16 – Ввод операций 4.2.2. Методы оптимизацииЗадачей дипломного проекта было реализовать 4 метода оптимизации из курса соответствующей дисциплины: Равномерный поиск; Поразрядный поиск; Метод дихотомии; Метод золотого сечения. Все эти методы относятся к разделу методов одномерной оптимизации. Задачей одномерной оптимизации является следующее: min {f(x) | a≤x≤b}, то есть найти число x*∈ [a;b], такое чтоf(x*) ≤ f(x), ∀x∈ [a;b]. Здесь а, b - заданные числа, причем а Поставленная задача может быть решена классическим методом, а именно; используя необходимое условие экстремума найдем все стационарные точки на интервале (а;b). Сравним значения функции f(x) в найденных точках, на концах отрезка [а;b] и в точках разрыва f'(х). Наименьшему из этих значений и будет соответствовать точка х* минимума функции f(х) на отрезке [а;b]. Однако, даже если функция f(х) задана аналитически и производная f'(х) найдена, то решение уравнения зачастую вызывает затруднения. Кроме того, вычисление производной может быть весьма трудоемко или же функция f(х) может быть задана не аналитически. Поэтому классический метод имеет ограниченное применение и для решения задачи на практике, как правило, применяют приближенные методы. 1. Метод равномерного поиска. Метод перебора, или метод равномерного поиска, является простейшим из прямых методов одномерной оптимизации и состоит в следующем. Отрезок [a;b] разбивается на n равных частей точками деления: xi= a + i (b – a) / n,i = 0…n. Сравнением значений функции f(x) во всех точках xi,i = ̅0̅,̅n находится точка xk, 0≤k≤n для которой f(xk) = min{f(x0),f(x1)…f(xn). Полагая x*≈xk,f* ≈ f(xk), получается решение задачи с погрешностью, не превосходящей величины Еn= (b-a)/n. Для того, чтобы обеспечить требуемую точность определения точки х*, число n отрезков разбиения необходимо выбирать из условия Еn≤E, т.е. назначить n = (b-a)/E. Программно этот алгоритм реализован с помощью цикла for (Рисунок 17). 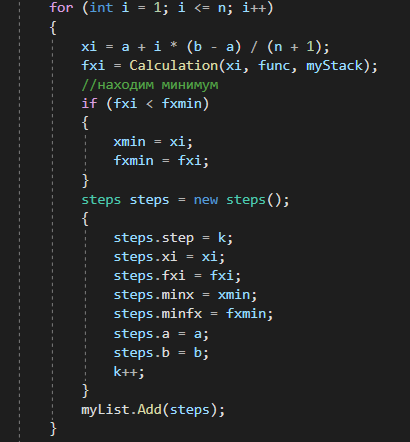 Рисунок 17 – Реализация равномерного поиска Здесь используется публичный класс steps.cs (Рисунок 18), который необходим для сохранения результатов каждой переменной на каждом шаге цикла алгоритма для того, чтобы затем их итерационно выводить в таблицу. 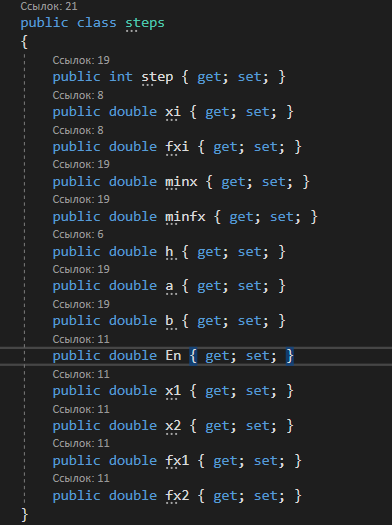 Рисунок 18 – Класс «steps» 2. Метод поразрядного поиска. Более усовершенствованный способ, так как в сравнении с предыдущим алгоритмом уменьшается количество значений функций f(x), которые необходимо находить в процессе минимизации. В методе поразрядного поиска перебор точек отрезка предлагается выполнять сначала с достаточно большим шагом h=xi+1 –xi>Е (например, h=(b - а)/4 ) до тех пор, пока не выполнится условие f(xi+1)≥f(xi) или пока очередная точка не совпадет с концом отрезка. После этого шаг уменьшается и перебор точек с новым шагом производится в противоположном направлении до тех пор, пока значения функции снова не перестанут уменьшаться или пока очередная точка не совпадет с другим концом отрезка. Описанный процесс завершается, когда перебор в данном направлении закончен, а использованный при этом шаг h не превосходит Е. Алгоритм выглядит следующим образом: Шаг 0. Задать параметр точности Е > 0, выбрать начальный шаг h=(b - а)/4, положить x0 = a, вычислить f(x0). Шаг 1. Найти очередную точку x1 =x0 + h, вычислить f(x1). Шаг 2. Сравнить значения функции f(x0) и f(x1) Если f(x0)>f(x1), то перейти к шагу 3, иначе - к шагу 4. Шаг3. Положить x1= x0 и f(x0)=f(x1). Проверитьусловие x0∈(a,b) Если a Шаг 4. Проверить условие окончания поиска |h| ≤E. Если оно выполняется, то вычисления завершить, положив x*≈x0, f*≈f(x0),иначе - перейти к шагу 5. Шаг 5. Изменить направление и шаг поиска, положив h = -h/4,x1= x0, f(x0)=f(x1). Перейти к шагу 1. Программно (Рисунок 19) алгоритм реализован согласно алгоритму, вычисления проводятся по шагам с использованием условного оператора if. Для перехода к шагам используется label.  Рисунок 19 – Часть кода реализации поразрядного поиска 3. Метод дихотомии. Относится к методам исключения отрезка, как и метод золотого сечения. Суть этого метода в том, чтобы делить очередной отрезок, содержащий точку минимума функции, пополам и исключать из рассмотрения ту часть, где минимума быть не может. Алгоритм данного метода следующий: Шаг 0. Задать параметр точности Е > 0, параметр алгоритма δ∈(0;2E) Шаг 1. Вычислить x1 иx2 по формулам: x1= 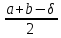 ; x2 = ; x2 =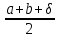 , где δ >0 - некоторое число, малое настолько, что еще можно отличить значения f(x1)иf(x2)друг от друга; , где δ >0 - некоторое число, малое настолько, что еще можно отличить значения f(x1)иf(x2)друг от друга;и значения функции f(x1)иf(x2). Шаг 2. Сравнить эти значения. Если f(x1)≤f(x2) , то перейти к отрезку [a; x2], положив b = x2, иначе - к отрезку [x1;b], положив a = x1. Шаг 3. Найти достигнутую точность En= (b-a)/2. Если En>E, то перейти к шагу 1 для выполнения следующей итерации, иначе завершить поиск, положив x* ≈ (a+b) / 2. Программно (Рисунок 20) этот алгоритм также реализован по шагам с использованием условного оператора ifи меток label. 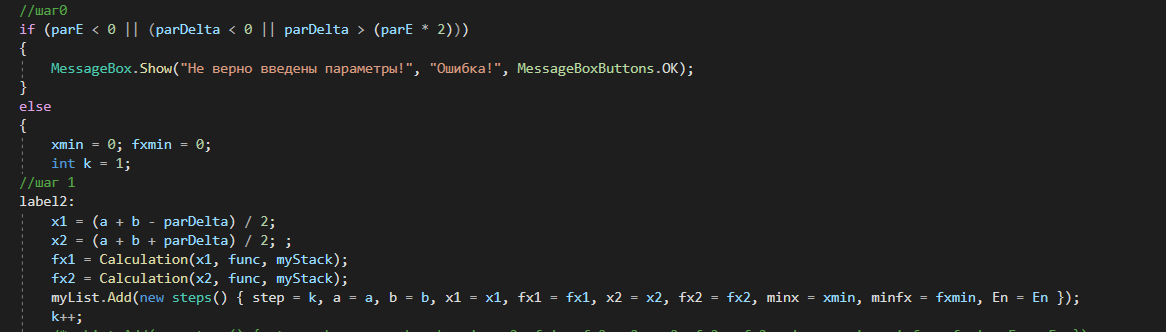 Рисунок 20 – Часть кода реализации метода дихотомии 4. Метод золотого сечения. В методе дихотомии при выполнении каждой итерации определяются две новые пробные точки x1 и x2. Рассмотрим такое симметричное их расположение на отрезке [а;b], при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением значения функции f(х) только в одной точке, т.к. другое значение уже найдено на предыдущей итерации. Таким свойством обладают точки золотого сечения отрезка [а;b]. Золотым сечением отрезка называется такое деление отрезка на две неравные части, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей частей отрезка. Алгоритм этого метода следующий: Шаг 0: Задать E> 0, 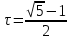 . .Шаг 1: Найти x1и x2по формулам: x1 = a + 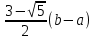 ; x2 = a + ; x2 = a + 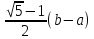 ; ;Вычислитьf (x1) и f (x2), En= 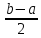 . .Шаг 2: Проверить условие окончания поиска En≤E. Если это условие выполняется, то перейти к шагу 4, иначе – к шагу 3. Шаг 3: Перейти к новому отрезку и к новым пробным точкам. Еслиf(x1) <f (x2), тоb = x2, x2 = x1, f(x2) = f (x1), x1 = b + a – x2, вычислить f(x1). Иначеa = x1, x1 = x2, f(x1) = f (x2),x2= b + a – x1, вычислитьf(x2).Положить En= 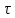 Enи перейти к шагу 2. Enи перейти к шагу 2.Шаг 4: Завершить поиск, положив x* ≈ (a+b) / 2. Программно (Рисунок 21) этот алгоритм также реализован по шагам с использованием условного оператора ifи меток label. 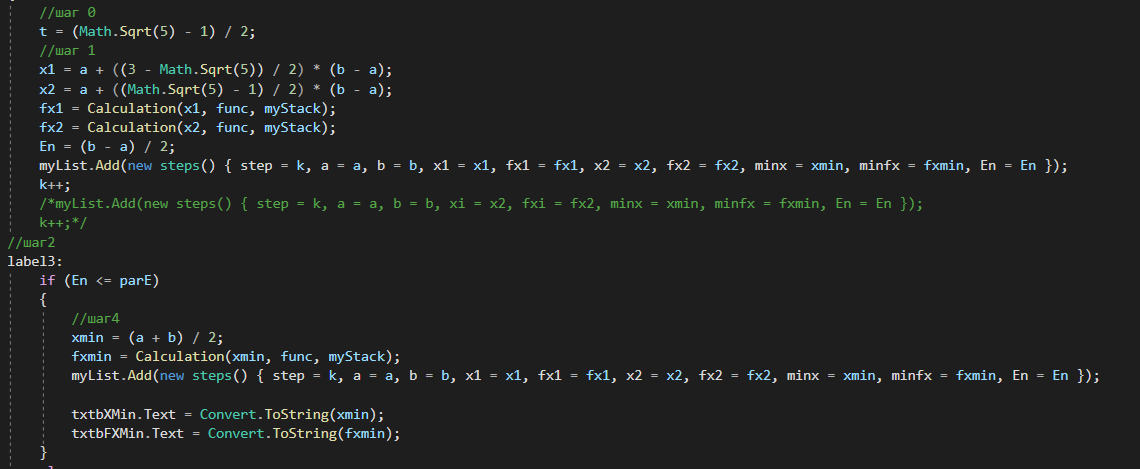 Рисунок 21 – Часть кода реализации метода золотого сечения |
