ИДЗ по физике Можно ли прочитать газету из космоса. Разрешающая способность
 Скачать 17.64 Kb. Скачать 17.64 Kb.
|
|
Можно ли прочитать газету из космоса? Разрешающая способность (разрешающая сила) оптических приборов, характеризует способность этих приборов давать раздельные изображения двух близких друг к другу точек объекта. Наименьшее линейное или угловое расстояние между двумя точками, начиная с которого их изображения сливаются, называется линейным или угловым пределом разрешения. Обратная ему величина обычно служит количественной мерой Р. с. Вследствие дифракции света на краях оптических деталей даже в идеальной оптической системе изображение точки есть не точка, а кружок с центральным светлым пятном, окруженным кольцами (попеременно тёмными и светлыми в монохроматическом свете, радужно окрашенными — в белом свете). Теория дифракции позволяет вычислить наименьшее расстояние, разрешаемое системой, если известно, при каких распределениях освещённости приёмник (глаз, фотослой) воспринимает изображения раздельно. Предел разрешения телескопов и зрительных труб выражают в угловых секундах для длины волны = 560 нм, соответствующей максимальной чувствительности человеческого глаза, он равен a"= 140/D (D в мм). Для фотообъективов Р. с. обычно определяют как максимальное количество раздельно видимых линий на 1 мм изображения стандартного тест-объекта и вычисляют по формуле N = 1470, где — относительное отверстие объектива. Приведённые соотношения справедливы лишь для точек, находящихся на оси идеальной оптической системы. Наличие аберраций и погрешностей изготовления увеличивает размеры дифракционных пятен и снижает Р. с. реальных систем, которая, кроме того, уменьшается по мере удаления от центра поля зрения. Диаметр зеркала космического телескопа Хаббла — 2,4 м, поэтому его теоретическое разрешение составляет 0,04 угловой секунды. Это обеспечивает гораздо более высокую детальность, чем для телескопа такого же размера, расположенного на поверхности Земли, поскольку космический телескоп Хаббла не подвержен влиянию атмосферной рефракции(преломления). Ни с Хаббла, ни с обычного земного телескопа не удаться рассмотреть газету из космоса, точнее прочитать. Слишком малое угловое разрешение. Для того чтобы прочитать буквы на ней , с разрешением Хаббла буквы должны быть с Египетские пирамиды. Хаббл предназначен для объектов, которые находятся далеко. Расстояние между буквами S = 0,001 метра. Высота на которой летают спутники 400 км = 400000 метров Самый большой телескоп в мире имеет зеркалом диаметром D= 39,3 метра, угловое разрешение = 0,005”, Давайте рассчитаем ,что он сможет увидеть при идеальных условиях без рефракции света, при длине волны 560 нм. 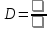 - необходимый диаметр главной линзы (объектива) ,м - необходимый диаметр главной линзы (объектива) ,м= 560 нм = 560* 10-9 метров Отсюда найдем значение арктангенса необходимого для дальнейших вычислений угла 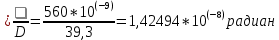 Между двумя буквами и направленным объективом образуется прямоугольный треугольник. С катетом S (расстояние между буквами) и h = 400000 метров – расстояние от буквы до объектива. Следовательно угловое разрешение будет отношением противолежащего катета s к прилежащему катету h. 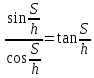 Найдем S ,зная 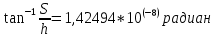 S= 0,00569976 м = 5 мм, что уже неплохо, но это при ИДЕАЛЬНЫХ условиях. Газету все равно не прочесть. Между буквами 1 мм. Найдем необходимый диаметр линзы 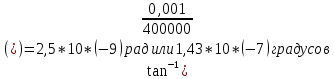 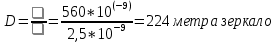 Но нужно учитывать рефракцию света, количество падающего света. При таких условиях диаметр зеркала должен быть в несколько десятков раз больше. Даже если смотреть с высоты 100 км (линия Кармана),то понадобится зеркало d= 56 метров при идеальных условиях. Таких зеркал у нас тоже нет. Вывод: Чтобы прочитать газету с высоты 400 км при идеальных условиях, понадобится зеркало D=224 метра. Таких зеркал у телескопов пока что нет. В наше время ,при наших технологиях, даже при идеальных условиях нельзя прочитать газету с высоты спутника. |
