"разветвленная цепь постоянного тока"
 Скачать 376.23 Kb.
|
  Министерство науки и высшего образования Российской Федерации федеральное государственное бюджетное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ МОРДОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. Н.П. ОГАРЁВА» (ФГБОУ ВО «МГУ им. Н.П. Огарёва») Институт электроники и светотехники Кафедра информационной безопасности и сервиса ОТЧЁТ ПО КОНТРОЛЬНОЙ РАБОТЕ №1 по дисциплине: Основы электротехники Автор отчёта о лабораторной работе ____________________ В. С. Горохова подпись, дата Обозначение лабораторной работы ЛР-02069964-430301-11-21 Направление подготовки 43.03.01 «Сервис» Руководитель работы ______________________ О. В. Кабанов подпись, дата Саранск 2021 "РАЗВЕТВЛЕННАЯ ЦЕПЬ ПОСТОЯННОГО ТОКА". Цель расчета: Изучение основных законов и методов анализа электрических цепей постоянного тока. Содержание работы: 1. Написать по законам Кирхгофа систему уравнений для определения неизвестных токов в ветвях схемы и решить ее на ЭВМ. 2. Определить неизвестные токи в ветвях схемы методом контурных токов и узловых потенциалов. 3. Составить баланс мощностей для исходной схемы. 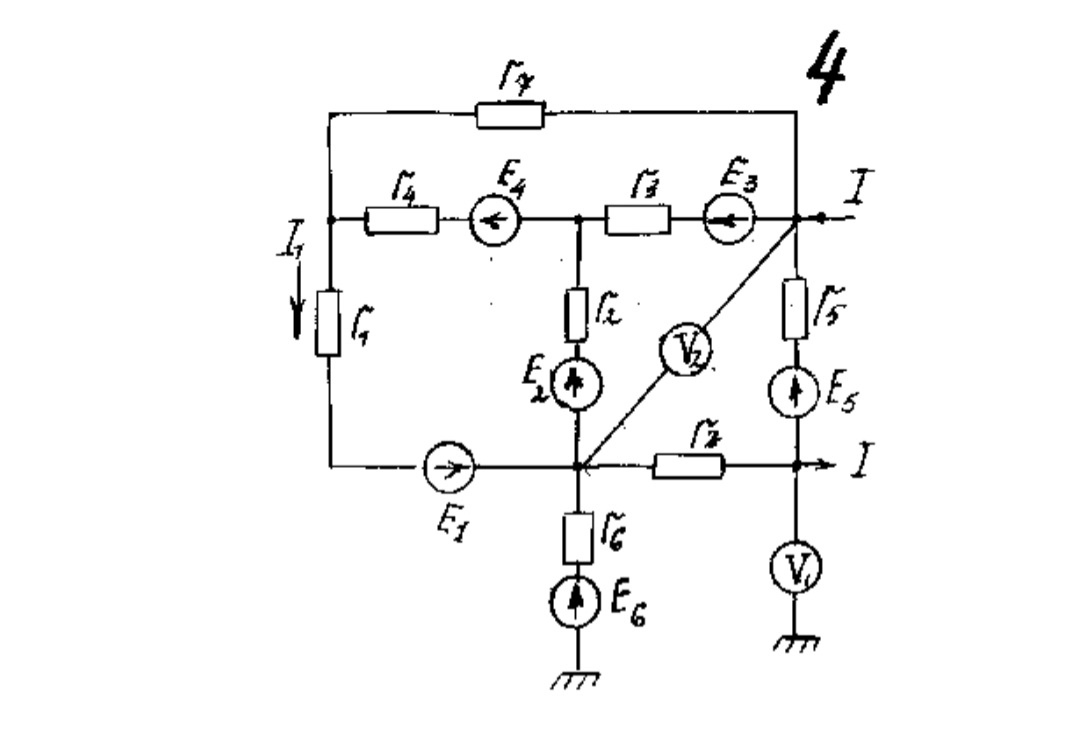 Рисунок 1 – Цепь постоянного тока. Таблица 1:Значение источников ЭДС и резисторов:
Написать по законам Кирхгофа систему уравнений для определения неизвестных токов в ветвях схемы и решить ее. Рассчитаем электрическую цепь, схема которой приведена задании. Цепь содержит четыре узла (у = 5) и семь ветвей (b = 7). По законам Кирхгофа составим систему уравнений и решим их. Изобразим расчетную схему цепи (рисунок 2), на которой показываем произвольно выбранные положительные направления токов в ветвях, а также направления обхода контуров. Обозначим узлы цепи буквами A, B, C, D. Уберём из цепи ветвь с R7 и вольтметры. 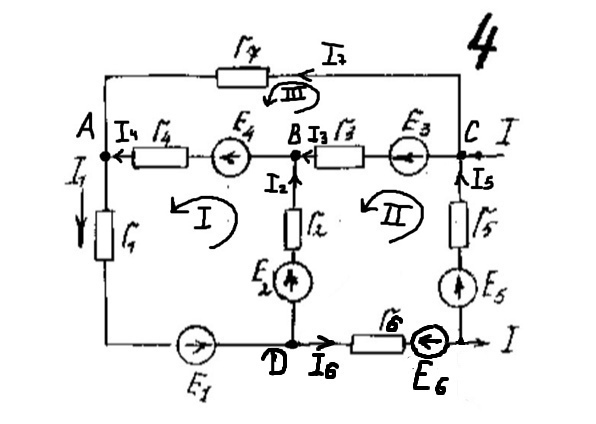 Рисунок 2 – Расчетная схема По первому закону Кирхгофа можно составить 3 независимых уравнения. Положительными считаем токи, направленные к узлу. Записываем эти уравнения для узлов A, B, C: A:-I1+I4 +I7=0 B: I2+I3-I4=0 C:- I3+I5-I7=0 По второму закону Кирхгофа можно составить уравнения для трех независимых контуров. Падение напряжения в сопротивлении считается положительным при условии, если направление тока в нем совпадает с произвольно выбранным направлением обхода контура, ЭДС источника считается положительной в том случае, если ее направление совпадает с направлением обхода контура. Контур, для которого составляется уравнение по второму закону Кирхгофа, должен быть независимым, т.е. отличаться от предыдущих хотя бы одной новой ветвью. Запишем уравнения по второму закону Кирхгофа: 1: I1R1 + I2R2 + I4R4 =E1+E2+E4 2:-I2R2 – I6R6 +I5R5+I3R3 = E5+E3-E2-E6 3: I7R7-I4R4-I3R3=-E3-E4 Подставим в уравнения числовые значения сопротивления и ЭДС: 1: 2I1+5I2+6I4=115 2: -5I2-3I6+2I5+4I3=30 3: 3I7-6I4-4I3=-140 Сформируем матрицу для решения данной системы уравнений с помощью доступных программных средств ЭВМ:     -1 0 0 1 0 0 1 0 0 1 1 -1 0 0 0 0 0 0 -1 0 1 0 -1 0 А= 2 5 0 6 0 0 0 B= 115 0 -5 0 4 2 3 0 30 0 0 4 6 0 0 3 -140 Получим: I1= 5,865 А I2=-1,3254 A I3=10,836 A I4=16,26 A I5=-0,752A I6=-13,258 A I7=2,95А Часть1'>Определить неизвестные токи в ветвях схемы методом контурных токов и узловых потенциалов. Часть1: 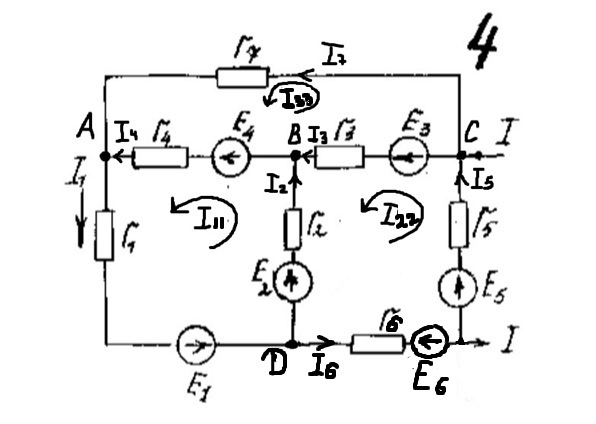 Рисунок 3 – Расчетная схема Так как в цепи три контура, то и уравнений будет 3. Получим уравнения: 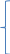 I11(R1+R2+R4)-I22R2-I33R4 =E2+E4 I22(R2+R3+R5+R7)-I11R2-I33R3 =E3-E2-E6+E5 I33(R3+R4+R7)-I11R4-I22R3= -E4-E3 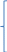 R142=(2+5+6)=13 R2357=(5+4+2+3)=14 R347=(4+6+3)=13 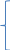 I11R142-I22R2-I33R4 =E2+E4 -I11R2+I22R2357-I33R3 =E3-E2-E6+E5 -I11R4-I22R3+I33R347= -E4-E3  I11*13-I22*5-I33*6 =30+80-I11*5+I22*14-I33*4 =60-30-20+20 -I11*6-I22*4+I33*13= -80-60 Сформируем матрицу для решения данной системы уравнений с помощью доступных программных средств ЭВМ:     13 -5 -6 110 A= -5 14 -4 B= 30 -6 -4 13 -140 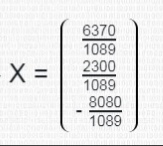 Решив матрицу данных уравнений, найдем контурные токи: I11=5,494 I22=2,1120 I33=-7,4196 Определим действительные токи в ветвях (их направление показаны на рисунке 3): I1= 5,494 А I2=-1,2374 A I3=10,5316 A I4=16,269 A I5=-0,7 A I6=-13,2 A I7=2,9 А Часть 2: 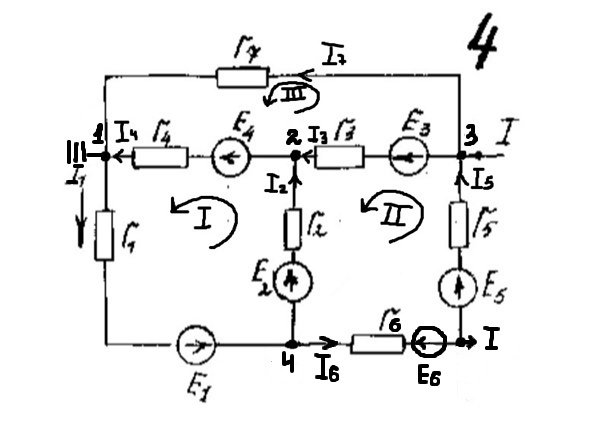 Рисунок 4 – Расчетная схема 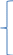 Приравняем потенциал узла 1 к нулю, т.е. считаем φ1 = 0. Составим систему уравнений относительно неизвестных потенциалов остальных трёх узлов. I2+I3-I4=0 - I3+I5-I7=0 I1-I2–I6=0 I1= (φ1- φ4+E1)/R1=(-φ4+E1)/R1 I2=(φ4- φ2+E2)/R2 I3=(φ3- φ2+E3)/R3 I4=(φ2- φ1+E4)/R4= (φ2+E4)/R4 I5=(φ4- φ3+E5)/R5 I6=( φ4- φ3-E6)/R6 I7=( φ3- φ1)/R7= φ3/R7 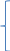 ((φ4- φ2+E2)/R2)+((φ3- φ2+E3)/R3)- ((φ2+E4)/R4)=0 -((φ3- φ2+E3)/R3)+ ((φ4- φ3+E5)/R5)- (φ3/R7)=0 ((-φ4+E1)/R1)- ((φ4- φ2+E2)/R2)- (( φ4- φ3-E6)/R6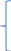)=0  (φ4/R2)-( φ2/R2)+(E2/R2)+( φ3/R3)-( φ2/R3)+(E3/R3)-( φ2/R4)-(E4/R4)=0-( φ3/R3)+( φ2/R3)-(E3/R3)+( φ4/R5)-( φ3/R5)+(E5/R5)-( φ3/R7)=0 -(φ4/R1)+(E1/R1)-( φ4/R2)+( φ2/R2)-(E2/R2) - (φ4/R6)+( φ3/R6)+(E6/R6)=0 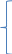 - φ2((1/R1)+(1/R3)+(1/R4))+ φ3(1/R3)+ φ4(1/R2)= -(E2/R2)-(E3/R3) φ2(1/R3)- φ3((1/R3)+(1/R5)+(1/R7))+ φ4(1/R5)= (E3/R3)-(E5/R5) φ2(1/R2)+ φ3(1/R6)- φ4((1/R1)+(1/R2)+(1/R6))= -(E1/R1)-(E6/R6) 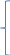 - φ2((1/2)+(1/4)+(1/6))+ φ3(1/4)+ φ4(1/5)= -(30/5)-(60/4) φ2(1/4)- φ3((1/4)+(1/2)+(1/3))+ φ4(1/2)= (60/4)-(20/2) φ2(1/5)+ φ3(1/3)-φ4((1/2)+(1/5)+(1/3))= -(5/2)-(20/3) 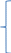 φ2(-0,91)+ φ3(0,25)+ φ4(0,2)= -21 φ2(0,25)- φ3(1,08)+ φ4(0,5)= 5 φ2(0,2)+ φ3(0,3)-φ4(1,03)= -9,1 Составим матрицу:  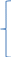   -0,91 0,25 0,2 -21 A= 0,25 1,08 0,5 B= 5 0,2 0,3 1,03 -9,1 Получим: φ2= 21,6 φ3=6,5 φ4= -14,9 I1=(-φ4+E1)/R1=(14,9+5)/2= 9,95 I2=(φ4- φ2+E2)/R2=(-14,9-21,6+30)/5= -1,3 I3=(φ3- φ2+E3)/R3=(6,5-21,6+60)/4= 11,225 I4=(φ2+E4)/R4=(21,6+80)/6= 16,93 I5=(φ4- φ3+E5)/R5=(-14,9-6,5+20)/2= -0,7 I6=(φ4- φ3-E6)/R6=(-14,9-6,5-20)/3= -13,8 I7=φ3/R7=6,5/3= 2,16 Составить баланс мощностей для исходной схемы. Мощность, вырабатываемая источниками энергии, равна: ΣР ист = E1I1 + E2I2 + E3I3 + E4I4 + E5I5+E6I6+E7I7; ΣР ист =9,95*5+(-1,3)*30+11,225*60+16,93*80+(-0,7)*20+(-13,8)*20+2,16*30= 34,51 Вт Мощность, потребляемая резисторами, равна: Σ Р потр = R1(I1)^2+ R2(I2)^2 + R3(I3)^2 +R4(I4)^2+ R5(I5)^2+R6(I)^2+R7(I7)^2; ΣР потр = 2*(9,95)^2+5*(-1,3)^2+4*(11,225)^2+6*(16,93)^2+2*(-0,7)^2+3*(-13,8)^2+3*(2,16)^2=33,89 Вт |