КРИПТОГРАФИЯ. Лабораторная работа 7- 8 БАС 18. Реализация на языке turbopascal ввода и вывода элементов массивов
 Скачать 140.16 Kb. Скачать 140.16 Kb.
|
|
Тема: Программирование типовых алгоритмов работы с элементами массивов. Цель: Освоить типовые алгоритмы и приемы программирования при работе с массивами. Задание: Дана матрица C[1:5; 1:6]. Определить: Среднеарифметическое отрицательных значений. Значение и номер минимального элемента третьей строки. Поменять местами минимальный и максимальный элементы в пятом столбце. Нулевые элементы матрицы заменить произведением положительных элементов. Ход работы: Данная задача является примером использования типовых алгоритмов работы с элементами массивов. Исходные данные для задачи: заданный массив C [5,6], размерность массива 2, размер по строкам 5, размер по столбцам 5. Индексы двухмерного массива i и j. Выходные данные: среднеарифметическое отрицательных значений СрАр, произведение положительных элементов ПрП, значение Мин3 и номер НМин3 минимального элемента третьей строки, значения Мин5, Макс5 и номера НМин5, НМакс5 минимального и максимального элементов в пятом столбце. Кроме того, в задаче необходимо использовать вспомогательные значения: k- количество отрицательных значений для определения среднеарифметического и Фл - флажок для выявления факта наличия в матрице нулевых элементов. 1. Типовые алгоритмы обработки массивов Рассматривая процедуры типовых алгоритмов, будем считать, что элементы массива введены в оперативную память. 1.1. Нахождение количества элементов, находящихся в заданном диапазоне, и определение суммы этих элементов Пример. Дан вектор А[1:10], состоящий из 10 элементов. Подсчитать количество элементов в диапазоне от -3 до +8 и сумму этих элементов. Фрагмент алгоритма: 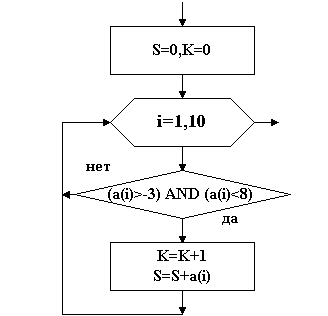 Рис. 35 S:=0; k:=0; For i:=1 to 10 do If (a[i]>-3) AND (a[i]<8) Then Begin k:=k+1;S:=S+ a[i];End; В данной процедуре сначала задаются начальные значения суммы S=0 и счетчика количества элементов K=0. Затем в цикле последовательно проверяются все элементы вектора на попадание в диапазон [-38]. При попадании очередного А[i] в этот диапазон, счетчик увеличивается на 1, а сумма - на величину А[i]. 1.2. Нахождение произведения и суммы элементов, удовлетворяющих заданному условию Пример. Дана матрица В[1:3,1:4]. Определить произведение положительных элементов и сумму отрицательных элементов. Фрагмент алгоритма: 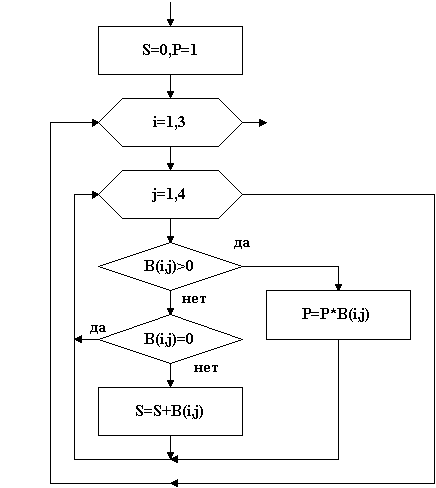 Рис. 36 Фрагмент программы: S:=0; P:=1; For i:=1 to 3 do For j:=1 to 4 do If b[i,j]>0 Then P:= P*b[i,j] Else If b[i,j]<>0 Then S:=S+b[i,j]; В данной процедуре сначала задают начальные значения суммы S=0 и начальное значение произведения Р=1. Задание начального значения Р=0 бессмысленно. Затем, в двух вложенных циклах последовательно проверяются все элементы матрицы и для B[i,j]>0 получают произведения, умножая предыдущее произведение на B[i,j], а для B[i,j]<0 получают сумму. Для выявления элементов B[i,j]=0 осуществляется дополнительная проверка. 1.3. Поиск минимального и максимального элементов массива Пример. Дана матрица В[1:4,1:5]. Определить минимальный и максимальный элементы массива и их координаты. Фрагмент алгоритма: 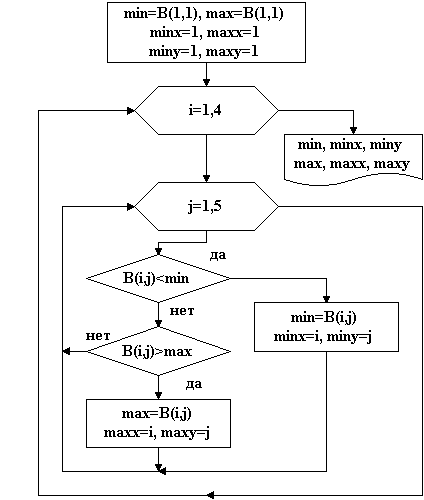 Рис. 37 Фрагмент программы: Min:= b[1,1]; Max:= b[1,1]; MinX:= 1; MaxX:=1; MinY:= 1; MaxY:=1; For i:=1 to 3 do For j:=1 to 4 do If b[i,j]>Max Then Begin Max:= b[i,j]; MaxX:= i; MaxY:=j; End; If b[i,j] Then Begin Min:= b[i,j]; MinX:= i; MinY:= j;End; WriteLn (‘МИНИМАЛЬНЫЙ ЭЛЕМЕНТ МАССИВА РАВЕН', Min:5:2); WriteLn (‘ОН РАСПОЛОЖЕН В ',MinX:1,’ СТРОКЕ И В ',MinY:1,' СТОЛБЦЕ') WriteLn (‘МАКСИМАЛЬНЫЙ ЭЛЕМЕНТ МАССИВА РАВЕН', Max:5:2); WriteLn (‘ОН РАСПОЛОЖЕН В ',MaxX:1,’ СТРОКЕ И В ',MaxY:1,' СТОЛБЦЕ') В данной процедуре сначала выделяют ячейки для минимального MIN и максимального MAX значений массива, а также для координат этих значений MINX, MINY для минимального значения и MAXX, MAXY для максимального и задаются их начальные значения. Для ячеек MIN и MAX в качестве начального значения удобно задать значение первого элемента массива. В том случае, если элементы массива еще не введены, в качестве начального значения MIN принимают очень большое число, например, +1000000, а в качестве начального значения MAX - очень малое число, например, -1000000. В качестве начальных значений координат задаются координаты первого элемента массива или нулевые значения. Далее во вложенных циклах последовательно выбираются значения элементов массива и сравниваются со значениями ячейки MIN. Если очередное значение B[i,j] меньше MIN, то значение ячейки MIN изменяется, в нем запоминается текущее значение B[i,j]. Одновременно в ячейках MINX и MINY запоминаются номер строки i и столбца j элемента B[i,j]. Если B[i,j] больше MIN, оно сравнивается со значением ячейки MAX. При B[i,j] больше MAX значение ячейки MAX изменяется, в нем запоминается B[i,j]. В ячейках MAXX и MAXY запоминаются координаты этого элемента. После выборки всех элементов массива и сравнения их с MIN и MAX на выходе вложенных циклов будут получены значения максимального MAX и минимального MIN элементов массива и их координаты. 1.4. Поиск минимального (максимального) элемента в строке (столбце) Пример. Дана матрица C[1:4,1:5]. Определить минимальный элемент в каждой строке. Фрагмент алгоритма:  Рис. 38 Фрагмент программы: For i:=1 to 3 do Begin Min:= c[i,1]; MinY:= 1; For j:=1 to 4 do If c[i,j] Then Begin Min:= c[i,j]; MinX:= i; MinY:= j;End; End; WriteLn (‘В ',i:1,’ СТРОКЕ МИНИМАЛЬНЫЙ РАВЕН ', Min:5:2); WriteLn (‘ОН РАСПОЛОЖЕН И В ',MinY:1,' СТОЛБЦЕ') В данной процедуре два вложенных цикла. Во внешнем цикле по строкам для каждой строки задается начальное значение ячеек MIN и MINY, в которых находится минимальное значение в строке и номер столбца, где находится этот элемент. Затем открывается цикл по столбцам, в котором последовательно выбираются в текущей строке элементы по столбцам и сравниваются со значением ячейки MIN. Если текущее значение C[i,j] меньше MIN, оно запоминается в ячейке MIN, и одновременно в ячейке MINY запоминается номер столбца этого элемента. После выбора всех элементов текущей строки на выходе цикла по столбцам будет получено минимальное в текущей строке значение MIN и номер столбца MINY, в котором это значение находится. Для нахождения максимального элемента в строке действия те же самые. Отличие в сравнении, где проверяется условие C[i,j]>MAX. Для нахождения минимального или максимального элемента в столбце, внешний и внутренний циклы меняются местами, а все остальные действия аналогичные. 1.5. Упорядочивание элементов последовательности по возрастанию (убыванию) Пример. Дан вектор A{5,3,-2,8,-6,0,-3,1} из восьми элементов. Расположить элементы вектора по возрастанию. Для упорядочивания используем метод "пузырька", при котором наиболее легкие элементы последовательно переходят в начало списка, то есть "всплывают". Процедура осуществляется следующим образом. Выбирается первый элемент последовательности (5) и последовательно сравнивается с оставшимися, для нахождения наименьшего. Найденный наименьший элемент (-6) меняется местами с первым (5) и становится в начале списка. Затем берется следующий элемент (3) и сравнивается с оставшимися для поиска минимального из оставшихся. После сравнения минимальный элемент (-3) ставится на место второго элемента (3). Такой процесс продолжается до конца последовательности, в результате чего элементы последовательности будут упорядочены по возрастанию (-6,-3,-2,0,1,3,5,8). Алгоритмически упорядочивание осуществляется в двух вложенных циклах. Во внешнем цикле осуществляется выбор элементов последовательности с первого до предпоследнего элемента. Сравнение этого элемента с оставшимися для поиска минимального осуществляется во внутреннем цикле. После окончания внутреннего цикла осуществляется перестановка найденного минимального и текущего элементов. Перестановка осуществляется по методу «трёх стульев», с временным помещением значения текущего элемента в ячейку S. Алгоритм упорядочения: 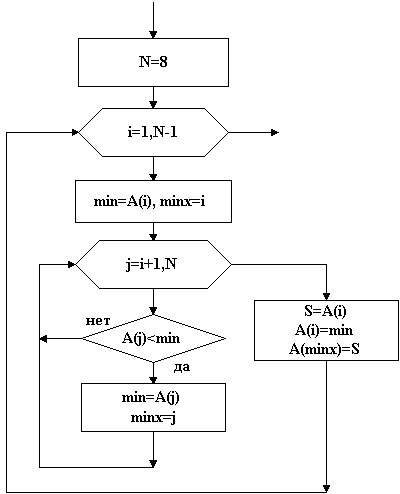 Рис. 38 Программа: Program Sort; Const n=8; A: Array [1..n] of Integer = (5,3,-2,8,-6,0,-3,1); Var i,j: Integer; s,Min,MinX: Integer; Begin WriteLn ('Неупорядоченный массив'); For i:=1 to n do Write(A[i]:2,’ ‘); WriteLn; For i:=1 to n-1 do Begin Min:= A[i]; MinX:=; For j:=i+1 to n do If A[j] s:= A[i]; A[i]:=Min; A[MinX]:=s; End; WriteLn ('Упорядоченный массив'); For i:=1 to n do Write(A[i]:2,’ ‘); WriteLn; End. Для упорядочения по убыванию необходимо во внутреннем цикле находить максимальный элемент, и помещать его вперед. 1.6. Формирование массива из элементов другого массива Пример. Дана матрица А[1:4,1:5], состоящая из элементов вещественного типа. Из элементов матрицы А, делящихся нацело на три, сформировать вектор В. В данной задаче необходимо объявить два массива – исходный двухмерный массив А[1..4,1..5] размером 45 и полученный одномерный массив В. Размер массива В заранее неизвестен, поэтому его размер должен заказываться максимальным, т.е. равным 20. Поскольку элементы матрицы имеют вещественный тип, то для поиска элементов, делящихся нацело на три, необходимо использовать условие INT(A[i,j]/3)=A[i,j]/3. В том случае, если число делится на три без остатка, функция INT, т.е. выделение целой части числа, совпадает с результатом деления этого числа на 3. Это же соотношение можно использовать при определении чисел, делящихся нацело на любое число. Фрагмент алгоритма: 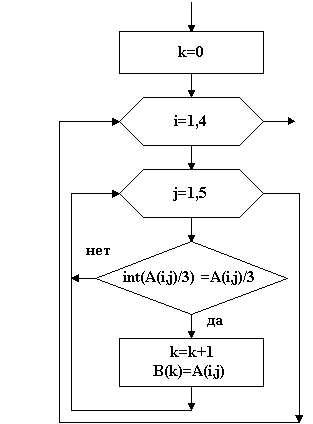 Рис. 39 Фрагмент программы: k:=0; For i:=1 to 3 do For j:=1 to 4 do If Int(a[i,j]/3)=a[i,j]/3 Then Begin k:=k+1; b[k]:=a[i,j];End; В данной процедуре перед началом формирования нового массива задается начальное значение К=0 счетчика индексов массива В. Новый массив В формируется путем последовательного выделения из элементов массива А элементов, делящихся нацело на 3. При нахождении такого элемента счетчик индексов К увеличивается на единицу, а затем формируется очередной элемент массива В. 1.7. Удаление элемента из массива Пример. Дан вектор В [1:10]. Если в векторе есть элемент, равный 0, удалить его. Данная задача разбивается на два этапа. На первом этапе находится номер элемента, равного нулю. На втором этапе этот элемент удаляется путем смещения всех элементов, начиная с нулевого, на одну позицию назад. Фрагмент алгоритма: 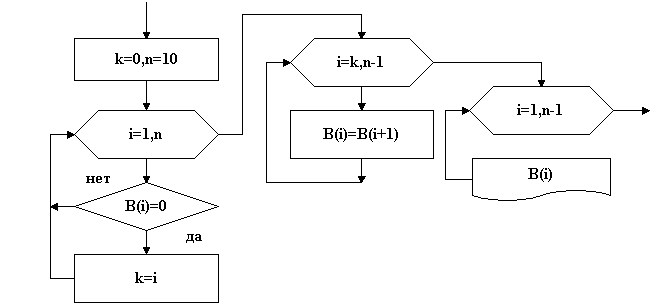 Рис. 40 Фрагмент программы: k:=0; n:=10; For i:=1 to n do If b[i]=0 Then k:=i; For i:=k to n-1 do b[i]:=b[i+1]; WriteLn ('Полученный массив'); For i:=1 to n-1 do Write(b[i]:2,’ ‘); WriteLn; В начале процедуры выделяется ячейка для запоминания номера нулевого элемента и задается ее начальное значение k=0. Нахождение нулевого элемента осуществляется путем последовательного перебора элементов массива. При нахождении такого элемента его номер запоминается в ячейке k. Сдвиг элементов назад осуществляется в цикле, начиная с номера нулевого элемента. Поскольку один элемент удаляется, то цикл сдвига должен быть короче на один элемент, т.е. до n-1. Новый вектор будет на один элемент короче, в связи с чем циклов печати будет так же на один меньше (до n-1). 1.8. Вставка элемента в массив Пример. Дан вектор В[1:10]. В массиве имеется элемент, равный 5. Вставить за этим элементом элемент, равный 5,5. Задача разбивается на три этапа. На первом этапе находится элемент, равный 5, и запоминается его номер в ячейке k. На втором этапе элементы, начиная с k+1, сдвигаются вперед на одну позицию. На третьем этапе в освободившуюся позицию k+1 вставляется элемент, равный 5,5. Фрагмент алгоритма представлен на рис. 8. 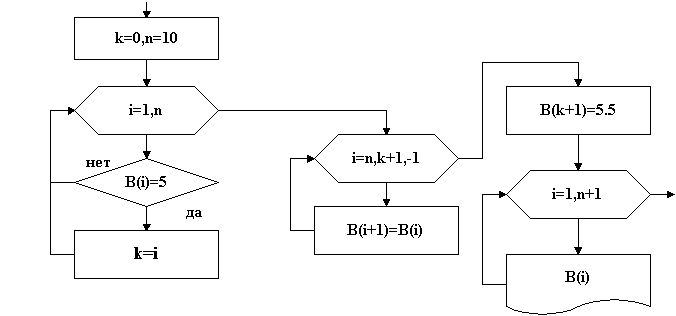 Рис. 40 Фрагмент программы: k:=0; n:=10; For i:=1 to n do If b[i]=5 Then k:=i; For i:=n downto k+1 do b[i+1]:=b[i]; B[k+1]:=5.5; WriteLn ('Полученный массив'); For i:=1 to n+1 do Write(b[i]:2,’ ‘); WriteLn; В данной процедуре сдвиг элементов на позицию вперед осуществляется с конца массива. Это связано с необходимостью сохранения элементов массива при сдвиге. При сдвиге вперед каждый предыдущий элемент сдвигается на освобожденное следующее место. Новый вектор будет на один элемент длиннее, в связи с чем циклов печати будет также на один больше (до n-1). 1.9. Удаление нескольких одинаковых элементов из массива Пример. Дан вектор В[1:10]. Удалить в векторе все нулевые элементы. Фрагмент алгоритма: 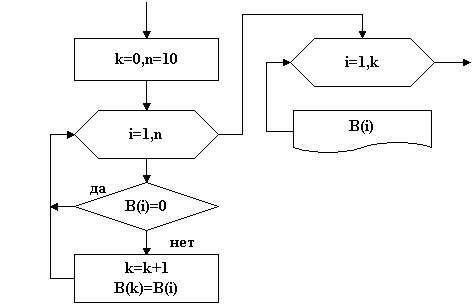 Рис. 41 Программа на TURBO-PASCAL: Program udalenie; Var A: Array[1..15] of Integer; i,k : Integer; Begin randomize; WriteLn('Исходный массив'); For i:=1 to 15 do Begin A[i]:=random(4)-2; Write(A[i]:1,' '); End; WriteLn; k:=0; For i:=1 to 15 do If A[i]<>0 Then Begin k:= k+1;A[k]:=A[i];End; WriteLn(‘Полученный массив'); For i:=1 to k do Write(A[i]:1,' '); WriteLn; End. Для удаления всех одинаковых элементов вводится дополнительный счетчик k, который играет роль счетчика индексов нового вектора, в котором удалены заданные элементы. В цикле происходит сравнение элементов исходного массива с заданным значением, при неравенстве элемент массива переносится в новый массив, а при равенстве отбрасывается. 1.10. Транспонирование матрицы Пример. Дана матрица А[1:5,1:5]. Если в матрице имеется элемент, меньше -3, транспонировать матрицу. Транспонированием матрицы называется замена строк столбцами. Транспонировать можно только квадратную матрицу. Транспонированную матрицу необходимо поместить в новый массив. Фрагмент алгоритма представлен на рис. 10. Фрагмент программы: f:=0; For i:=1 to 5 do For j:=1 to 5 do If a[i,j]<-3 Then Begin f:=1; break; End; If f=1 Then Begin For i:=1 to 5 do For j:=1 to 5 do b[i,j]:=a[j,i]; WriteLn (‘Транспонированная матрица'); For i:=1 to 5 do Begin For j:=1 to 5 do Write(b[i,j]:5:2,’ ‘); WriteLn; End; End Else WriteLn (‘Нет элемента меньше -3');  Рис. 42 В данной задаче для выявления наличия элемента, меньшего –3, используется так называемый флаг. Для этого в начале процедуры выделяется ячейка под флаг F. Начальное значение флага устанавливается равным 0 (флаг "опущен"). Если в массиве А окажется хотя бы один элемент, меньший -3, F принимает значение, равное 1 (флаг "поднят"), при этом прерывается цикл процедурой break. В зависимости от значения F, транспонирование матрицы либо осуществляется (F=1), либо нет (F=0). Транспонирование матрицы осуществляется присвоением b[i,j]:=a[j,i]. |
