Реализация вычисленной задачи в различных программных пакетах
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Реализация вычисленной задачи в различных программных пакетах Формулировка задачи Дан треугольник, заданный координатами своих вершин. Для этого треугольника вычислить: длины сторон; периметр; площадь; величины углов в градусах. Математическая подстановка задачи Рассмотрим треугольник ABC, заданный координатами вершин на плоскости 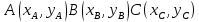 Условие осуществления треугольника: треугольник существует, если сумма двух любых длин его сторон больше длины третьей стороны. Для вычисления характеристик треугольник используются следующие формулы: Длины сторон: AB=с= 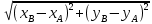 BC=a=  AC=b= 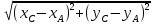 Периметр: p= 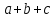 . .Площадь (формула Герона): s= 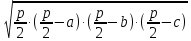 Величины углов (в радианах): A=  , B= , B=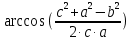 , ,C= 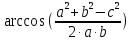 . .Реализация задачи в среде Excel На рисунке 1 показана электронная таблица, используемая для решения поставленной задачи. Пользователь вводит координаты вершин треугольника в диапазон ячеек B2:C4. На основе введенных данных вычисляются характеристики треугольника, проверяется условие его существования. На рисунке 1а показан вид листа электронной таблицы, если треугольник существует. На рисунке 1б вид таблицы для того, когда треугольник не существует (при этом все вычисления скрыты от пользователя) а) 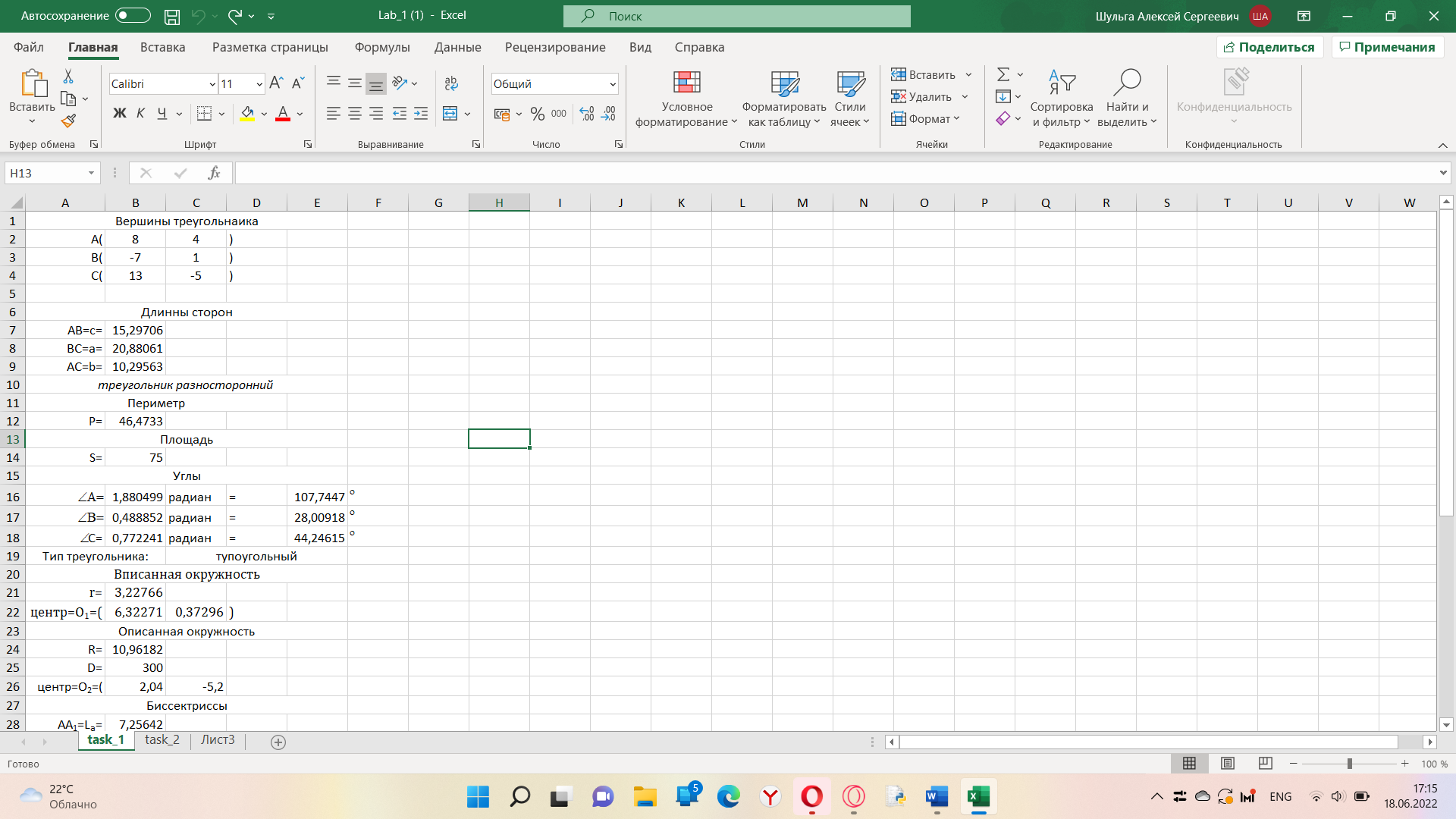 б) б)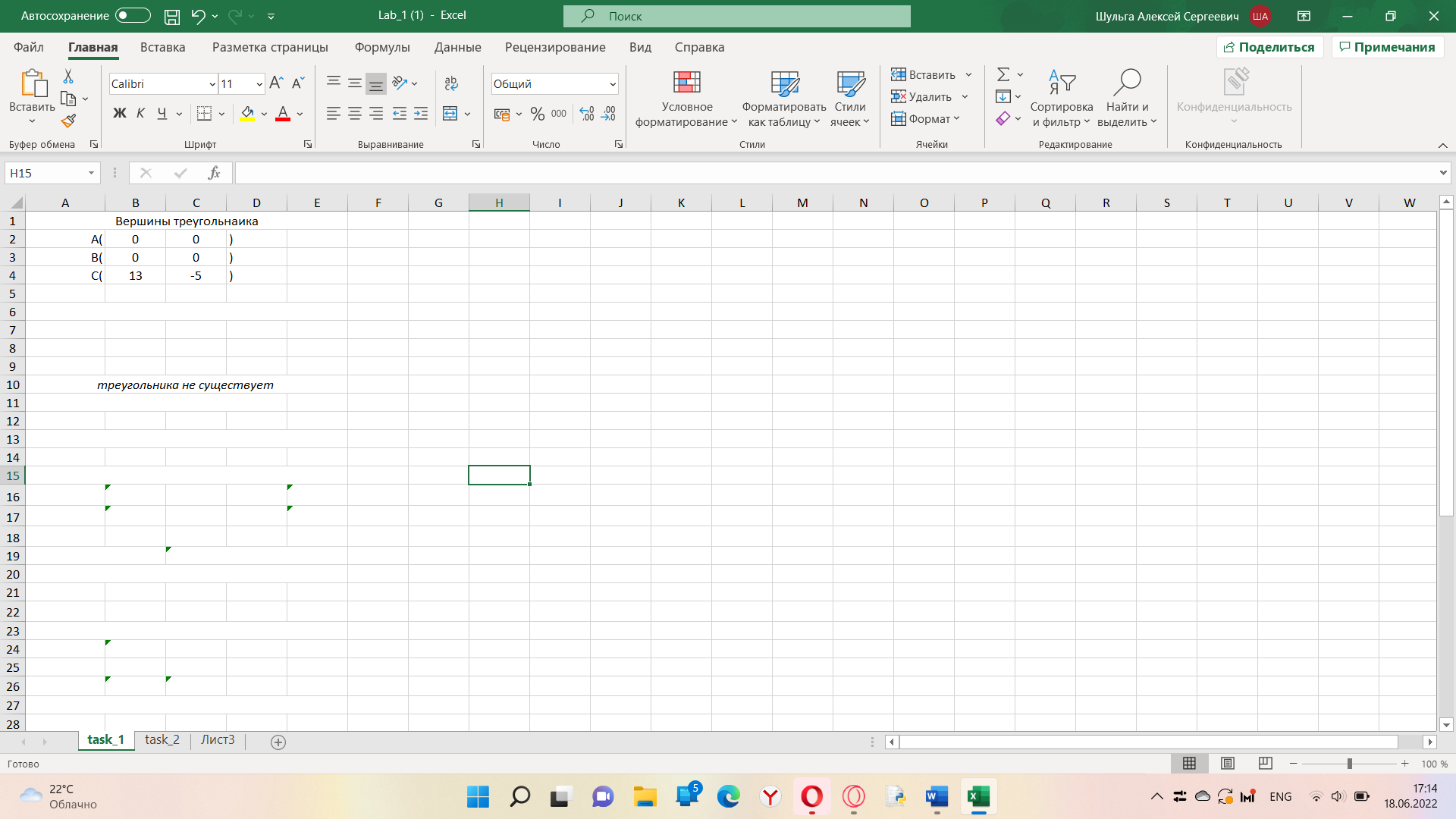 а) треугольник существует; б) треугольник не существует. Рисунок 1 Лист электронной таблицы с расчётами При реализации задачи использовались следующие формулы: для вычисления длин сторон: B7: =КОРЕНЬ((B2-B3)^2+(C2-C3)^2) B8: =КОРЕНЬ((B4-B3)^2+(C4-C3)^2) B9: =КОРЕНЬ((B4-B2)^2+(C4-C2)^2) для проверки существования треугольника: =ЕСЛИ(ИЛИ(B7+B8<=B9;B8+B9<=B7;B7+B9<=B8); "Треугольника не существует";"Треугольник существует") для вычисления периметра: B12: =B7+B8+B9 для вычисления площади: B14: =КОРЕНЬ(B12/2*(B12/2-B7)*(B12/2-B8)*(B12/2-B9)) для вычисления углов: B16: =ACOS((B7^2+B9^2-B8^2)/(2*B7*B9)) B17: =ACOS((B7^2+B8^2-B9^2)/(2*B7*B8)) B18: =ACOS((B8^2+B9^2-B7^2)/(2*B8*B9)) Результаты вычислений В таблице 1 представлены результаты вычислений в среде Excel для различных входных данных. Таблица 1 Результаты вычислений
Реализация задачи в среде MathCAD На рисунке 2 показана страница документа MathCAD, используемая для решения поставленной задачи. Пользователь вводит координаты вершин треугольника в раздел «Координаты Вершин треугольника ABC», присваивая переменянным 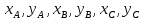 необходимые значения. На основе введённых данных вычисляют характеристики треугольника, проверяется условие его существования. необходимые значения. На основе введённых данных вычисляют характеристики треугольника, проверяется условие его существования. Рисунок 1 Страница документа MathCAD с расчётами При реализации задачи использовались следующие формулы: для вычисления длин сторон: 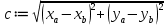 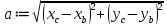  для проверки существования треугольника: 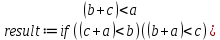 “Треугольник не существует” Else “Треугольник существует” для вычисления периметра: 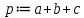 для вычисления площади: 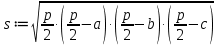 для вычисления углов: 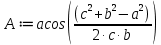  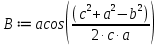 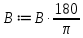  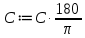 Результаты вычислений В таблице 2 представлены результаты вычислений в среде MathCAD для различных входных данных. Таблица 2 Результаты вычислений
Реализация задачи в среде Python На рисунке 3 код программы на языке Python, используемый для решения поставленной задачи. Пользователь вводит координаты вершин, которые записываются в переменные вещественные переменные 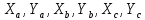 . Затем вычисляются длины сторон треугольника, проверяется условие его существования и в случае, если треугольник существует, выводятся его характеристики. Если треугольник не существует выводится сообщение. На рисунке 4 показаны результаты выполнения программы для различных входных данных. . Затем вычисляются длины сторон треугольника, проверяется условие его существования и в случае, если треугольник существует, выводятся его характеристики. Если треугольник не существует выводится сообщение. На рисунке 4 показаны результаты выполнения программы для различных входных данных. Рисунок 3 Код программы а)  б) б) а) треугольник существует; б) треугольник не существует. Рисунок 4 Результат выполнения программы При реализации задачи использовались следующие формулы: для вычисления длин сторон: a = math.sqrt((Xb-Xc)**2 +(Yb-Yc)**2) b = math.sqrt((Xa-Xc)**2 +(Ya-Yc)**2) c = math.sqrt((Xa-Xb)**2 +(Ya-Yb)**2) для проверки существования треугольника: if a + b <= c or a + c <=b or c + b <= a: print("Треугольник не существует!") else: print("Длинны сторон : a=", round(a,3),"," "b=", round(b,3) ,"," "c=", round(c,3)) для вычисления периметра: p = a+b+c print("p = ", round(p,3)) для вычисления площади: s = math.sqrt((p/2)*((p/2)-a)*((p/2)-b)*((p/2)-c)) print("s = ", round(s,3)) для вычисления углов: AUa = math.degrees(math.acos(((c**2)+(b**2)-(a**2))/(2*c*b))) BUb = math.degrees(math.acos(((c**2)+(a**2)-(b**2))/(2*c*a))) CUc = math.degrees(math.acos(((b**2)+(a**2)-(c**2))/(2*b*a))) print("Углы : uA =", round(Ua,3),"," "uB =", round(Ub,3) ,"," "uC =", round(Uc,3)) Для вычисления тупоугольного, прямоугольного и остроугольного прямоугольника: if (abs(uA-90)<0.000001 or abs(uB-90)<0.000001) or abs(uC-90)<0.000001: print ("Треугольник прямоугольный") elif (uA>90) or (uB>90) or (uC>90): print("Треугольник тупоугольный") else: print("Треугольник остроугольный") Результаты вычислений В таблице 3 представлены результаты вычислений в среде Python для различных входных данных. Таблица 3 Результаты вычислений
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
