реферат по электродинамике, магнетики. реферат. Реферат 2 по электродинамике тема 1 магнетики Магнетик вещество, обладающее магнитными свойствами
 Скачать 122.43 Kb. Скачать 122.43 Kb.
|
|
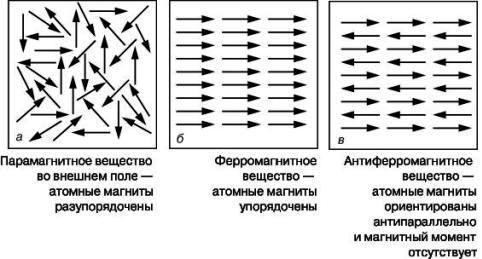
РЕФЕРАТ № 2 по электродинамике ТЕМА 1: «МАГНЕТИКИ» 1. Магнетик – вещество, обладающее магнитными свойствами. Намагничивание вещества зависит от его природы. В макроскопической электродинамике намагничивание характеризуется вектором намагничения или намагничивания М. Вектор намагничения М есть средний магнитный момент единицы объема вещества. 2. Связь вектора намагничения с напряженностью магнитного поля: 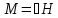 Где, ꭓ - магнитная восприимчивость вещества Магнитная восприимчивость — физическая величина, выражающая отношение между магнитным моментом единицы объёма (намагниченностью) вещества и напряжённостью магнитного поля в этом веществе. По значению магнитной восприимчивости Фарадей все вещества разбил на три группы: Если ꭓ > 0, но ꭓ << 1, то такое вещество называется – парамагнетик; Если ꭓ > 0, но ꭓ >> 1, то такое вещество называется – ферромагнетик; Если ꭓ ˂ 0, то такое вещество называется – диамагнетик. Эта классификация является устаревшей, так как не учитывает многообразия магнетиков, обнаруженных в настоящее время. К тому же эта классификация основана на феноменологической величине ꭓ, определяемой из опыта, и не учитывает микроструктуру вещества. 3. Магнитный порядок – это определенная взаимная ориентация друг по отношению к другу магнитных моментов атомов, молекул, ионов или электронов. Все магнетики на две большие группы: 1. Магнитонеупорядоченные, 2. Магнитоупорядоченные. К 1-й группе относятся вещества, у которых в отсутствие внешнего магнитного поля нет магнитного порядка. Ко 2-й относятся вещества, у которых в отсутствие внешнего магнитного поля имеется определённый магнитный порядок. 4. «Магнитонеупорядоченные вещества»
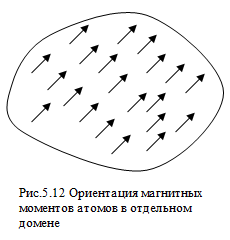
5. Сравнение ферро- и антиферромагнетиков, относящихся к классу магнитоупорядоченных веществ 6. Ферримагнетики – это вещества, которые, как и антиферромагнетики, имеют антипараллельное упорядочение. Однако магнитные моменты моменты ближайших соседей по величине различны и поэтому не компенсируют друг друга. Этим ферримагнетик и отличается от антиферромагнетиков. Примеры ферритов: порошкообразные соединения типа 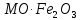 , где M – двухвалентный металл. , где M – двухвалентный металл. Ферриты, как и магнитные сплавы, имеют доменную структуру и высокую магнитную проницаемость. Вместе с тем в отличие от магнитных сплавов ферритам, свойственно высокое электрическое сопротивление и, как следствие, малые потери энергии при перемагничивании, что делает их незаменимыми в технике высоких и сверхвысоких частот. Благодаря сочетанию высоких магнитных свойств и низкой электропроводности ферриты широко применяются в технике высоких частот (более 100 кГц). Ферриты используют в качестве магнитных материалов в радиотехнике, электронике, автоматике, вычислительной технике (ферритовые поглотители электромагнитных волн, антенны, сердечники, элементы памяти, постоянные магниты и т. д.) В звуковой технике, в основном, находится феррит стали. Он же присутствует и в видеоаппаратуре. Кабели мониторов, видеокамер, принтеров, прочей компьютерной аппаратуры. 7. Неколлинеарные магнитные структуры. Сложное неколлинеарное упорядочение обнаружено в редкоземельных элементах: спиральная (геликоидальная) и зонтичная (циклоидальная) магнитные структуры. 1. Антиферромагнитный геликоид (спираль) наблюдается в димпрозии, гольмии, тербии. Приведите примеры веществ циклоидальной магнитной структурой. Примеры веществ с геликоидальной магнитной структурой: редкоземельные элементы, сплав 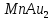 , двуокись марганца , двуокись марганца 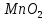 , также эти структуры были обнаружены ы некоторых составах сплава , также эти структуры были обнаружены ы некоторых составах сплава 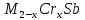 , эрбиевом феррите – гранате, хромите марганца, соединение , эрбиевом феррите – гранате, хромите марганца, соединение 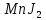 и т.д. и т.д.ТЕМА 2: Механические силы в магнитостатике (сила Лоренца, сила Ампера) На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, равная: 𝐹 = 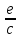 [𝜗 𝐵 ] (*) [𝜗 𝐵 ] (*)Сила действует перпендикулярно скорости частицы и поэтому не совершает работы по её перемещению. Однако движение частицы под действием силы Лоренца становится финитным. Действием силы Лоренца объясняются многие явления природы. Найдём силу, действующую на ток в магнитном поле (сила Ампера), используя (*) для элемента заряда 𝑑𝑞 = 𝜌𝑑𝑉: 𝑑𝐹 = 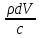 [𝜗 𝐵 ] = [𝜗 𝐵 ] = 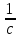 [𝜌𝜗 𝐵 ]𝑑𝑉 = [𝜌𝜗 𝐵 ]𝑑𝑉 = 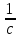 [𝑗 𝐵 ]𝑑𝑉 [𝑗 𝐵 ]𝑑𝑉Тогда сила равна: 𝐹 = 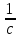 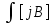 𝑑𝑉. 𝑑𝑉.Формула показывает, что согласно свойству векторного произведения, 𝐹 перпендикулярна 𝑗 и 𝐹 перпендикулярна 𝐵 , и даёт обоснование правила левой руки. Для линейного тока, проведя обычную замену 𝑗𝑑𝑉 = 𝐽𝑑𝑙 , получаем: 𝐹 = 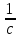 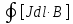 𝑑𝑉= 𝑑𝑉= 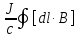 . .Итак, 𝐹= 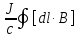 . . |

 ,
, 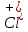 … и
… и  ,
, 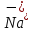 …
…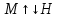 ).
).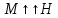 ).
).