Диплом. Автоматизация процесса осушки газа на установке комплексной подг. Реферат дипломный проект 104 с., 24 рисунка, 17 таблиц, 11 использованных источников, 1 приложение
 Скачать 7.56 Mb.
|
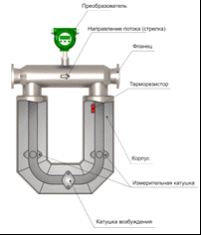 Рисунок 4.1 - Устройство кориолисого расходомера Сенсор напрямую измеряет расход, плотность среды и температуру сенсорных трубок. Преобразователь конвертирует полученную с сенсора информацию в стандартный выходной сигнал. Измеряемая среда, поступающая в сенсор, разделяется на равные половины, протекающие через каждую из сенсорных трубок. Движение катушки возбуждения приводит к тому, что трубки колеблются вверх-вниз в противоположном направлении друг другу. Измерительные катушки устанавливают на боковых ответвлениях одной расходомерной трубки, а магниты устанавливают на боковых ответвлениях противолежащей расходомерной трубке. Каждая катушка движется в однородном магнитном поле соседнего магнита. Напряжение, генерируемое каждой измерительной катушкой, создает синусоидальное колебание отражающее движение одной трубки относительно другой. В условиях отсутствия потока движения на входном и на выходном концах трубки находятся в одной фазе, синусоидальные колебания совпадают, эффект Кориолиса не возникает. При наличии потока синусоидальные колебания различаются по фазе, поскольку сигнал на выходной ветви запаздывает относительно сигнала на ветви на выходе (рисунок 4.2). 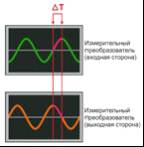 Рисунок 4.2 - Запаздывание сигнала на входной и выходной ветви Время запаздывания ΔТ измеряется в микросекундах и всегда пропорционально массовому расходу. Соотношение между массой и собственной частотой колебаний сенсорной трубки - это основной закон измерения плотности в кориолисовых расходомерах. В рабочем режиме катушка возбуждения питается от преобразователя, при этом сенсорные трубки колеблются с их собственной частотой. Как только масса измеряемой среды увеличивается, собственная частота колебаний трубок уменьшается соответственно, при уменьшении массы измеряемой среды, собственная частота колебаний трубок увеличивается. Частота колебаний трубок зависит от их геометрии, материала, конструкции и массы. Масса состоит из двух частей: массы самих трубок; массы измеряемой среды в трубках. Для конкретного типоразмера сенсора масса трубок постоянна. Поскольку масса измеряемой среды в трубках равна произведению плотности среды и внутреннего объема, а объем трубок является также постоянным для конкретного типоразмера, то частота колебаний трубок может быть привязана к плотности среды и определена путем измерения периода колебаний. Частота колебаний измеряется выходным детектором (рисунок 4.3) в циклах в секунду (Гц). 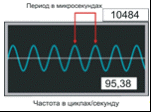 Рисунок 4.3 - Частота колебаний измерительных трубок Период колебаний, как известно, обратно пропорционален частоте. Измерить время цикла легче, чем считать количество циклов, поэтому преобразователи вычисляют плотность измеряемой жидкости, используя период колебаний трубок в микросекундах. Плотность прямо пропорциональна периоду колебаний сенсорных трубок. 4.2 Кориолисовый расходомер Micro Motion СMF Предлагается использовать кориолисовый расходомер Micro Motion СMF, основные технические характеристики которого представлены в таблице 4.1. Таблица 4.1 - Основные технические характеристики Micro Motion СMF
Информация об измеряемых величинах может считываться с жидкокристаллического индикатора (ЖКИ), а так же передаваться в виде аналогового сигнала (4..20 мА), аналогово-цифрового сигнала с использованием HART протокола или RS485. .3 Расчет коэффициентов передаточной функции по переходной кривой Необходимо определить оптимальные параметры настройки регулятора в одноконтурной системе автоматического регулирования (САР) расхода РДЭГ, подаваемого в абсорбер А-201. Расчет производим по кривой переходного процесса в специальных программах анализа и синтеза систем автоматического регулирования. На рисунке 4.4 приведена кривая переходного процесса расхода ДЭГ в абсорбер А-201, которая наиболее приближена к реальной. 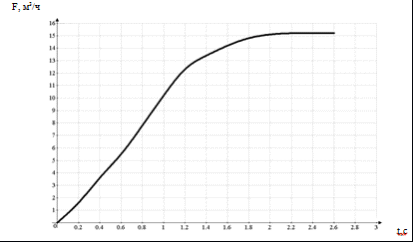 Рисунок 4.4 - Кривая переходного процесса расхода ДЭГа в абсорбер Значения кривой переходного процесса приведены в таблице 4.2. Таблица 4.2 - значения кривой переходного процесса
Определим параметры модели объекта методом «площадей» Симою М.П. по переходной кривой. Математической моделью называется система математических соотношений (уравнений), устанавливающих связь между входными и выходными сигналами объекта. В данном случае общий вид модели будет следующий:  ,(4.1)где  - нормированная передаточная функция;  - коэффициент передачи  ;  - время запаздывания (по исходным данным).Нормированной передаточной функции соответствует нормированная переходная характеристика s(t), которая определяется как отношение текущего значения выходного сигнала к его установившемуся значению: .(4.2)Для определения коэффициентов  и  нормированной передаточной функции используется метод «площадей» Симою: ,(4.3) где  - «площади» Симою, вычисляются по переходной кривой.При известных «площадях» Симою, задаваясь определённой структурой модели можно определить её параметры (коэффициенты). «Площади» Симою определяются с помощью вспомогательной j(t) функции:  ,(4.4) ,(4.5) ,(4.6) ,(4.7) ,(4.8) .(4,9)где  - моменты вспомогательной функции.Если из выражения (4.6) выразить  , а затем приравнять правые части уравнений (4.3) и (4.6), то легко найти связь между моментами вспомогательной функции и «площадями» Симою: .(4.10)Так  - площадь под кривой вспомогательной функции.Для расчета параметров модели методом площадей введем нормированную переходную кривую, координаты точек которой приведены в таблице 4.3, определяемую формулой:  .(4.11)Таблица 4.3 - Координаты точек нормированной переходной кривой
Нормированная переходная кривая изображена на рисунке 4.5. Введем в рассмотрение вспомогательную функцию  , рисунок 4.5 координаты точек которой приведены в таблице 4.4, определяемую формулой:  .(4.12)Таблица 4.4 - Координаты точек вспомогательной кривой
Рассчитаем площадь S1, ∆t = 1,n = 12:  ,где Dt = 1 мин - шаг по времени. Полученное значение и есть значение «площади» Симою S1. Вспомогательная кривая разгона представлена на рисунке 4.6. 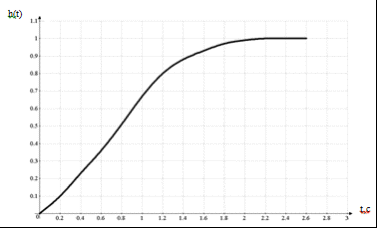 Рисунок 4.5 - Нормированная переходная кривая 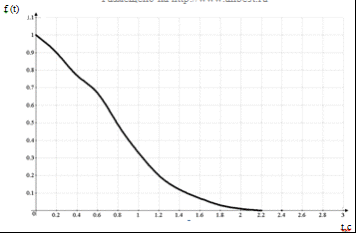 Рисунок 4.6 - Вспомогательная кривая разгона Определение параметров модели по площадям Приведем передаточную функцию модели:  ,(4.13) .(4.14)Раскрывая скобки в правой части и приводя подобные члены, получим степенной ряд  (4.15)Приравнивая в последнем равенстве коэффициенты при одинаковых степенях s слева и справа, получим линейную систему уравнений для определения коэффициентов модели  : ,(4.16)Расчет площадей Симою и коэффициентов нормированной передаточной функции проводим с помощью программы SIMOU.EXE. Определение параметров передаточной функции по виду переходного процесса методом площадей Симою Число точек переходной кривой M = 11; шаг квантования по времени DT = 0.20000; значения переходной кривой:( 1) = 0.000000;( 2) = 1.600000;( 3) = 5.500000;( 4) = 7.800000;( 5) = 10.200000;( 6) = 12.300000;( 7) = 13.400000;( 8) = 14.200000;( 9) = 14.800000;(10) = 15.100000;(11) = 15.200000. Результат расчета: коэффициент усиления передаточной функции KY= 15.200000; значения площадей:( 1 ) = 0.803509;( 2 ) = 0.212293;( 3 ) = 0.004182;( 4 ) = - 0.053377;( 5 ) = - 0.078474. Вариант 1 полином числителя п.ф.:( 0 ) = 1.0;( 1 ) = - 1.448233;( 2 ) = - 0.279958. Полином знаменателя п.ф.: A ( 0 ) = 1.0;( 1 ) = - 0.644725;( 2 ) = - 0.671418;( 3 ) = - 0.078320. Вариант 2 полином числителя п.ф.:( 0 ) = 1.0;( 1 ) = - 1.470165. Полином знаменателя п.ф.: A ( 0 ) = 1.0;( 1 ) = - 0.666657;( 2 ) = - 0.968998;( 3 ) = - 0.307924;( 4 ) = - 0.059525. Вариант 3 полином числителя п.ф.:( 0 ) = 1.0;( 1 ) = - 1.049597;( 2 ) = - 0.272107. Полином знаменателя п.ф.:( 0 ) = 1.0;( 1 ) = - 0.246088;( 2 ) = - 0.358960. Вариант 4 полином числителя п.ф.:( 0 ) = 1.0;( 1 ) = 12.734810. Полином знаменателя п.ф.: A ( 0 ) = 1.0;( 1 ) = 13.568320;( 2 ) = 10.468930;( 3 ) = 2.714062. Вариант 5 полином числителя п.ф.:( 0 ) = 1.0;( 1 ) = - 0.019697. Полином знаменателя п.ф.:( 0 ) = 1.0;( 1 ) = 0.793811;( 2 ) = 0.196466. Из дальнейшего рассмотрения исключаем 1-й, 2-й, 3-й варианты передаточной функции, так как они не устойчивы по критерию Стодолы (среди коэффициентов характеристического полинома встречаются не положительные). Расчет и построение переходных кривых моделей. Выбор рабочей модели Переходные кривые моделей можно рассчитать по найденным передаточным функциям с помощью программы LAPNEW.EXE или методом обратного преобразования Лапласа. Результаты расчета переходных процессов, рассчитанных на ЭВМ, приведены ниже. Модель 4. Корни характеристического полинома:( 1) = - 0.078330, ImS( 1) = 0.000000;( 2) = - 1.899724, ImS( 2) = - 1.058000;( 3) = - 1.899724, ImS( 3) = 1.058000. Координаты точек переходного процесса приведены в таблице 4.5 Таблица 4.5 - Координаты точек вспомогательной кривой
Модель 5 Корни характеристического полинома:( 1) = - 1.950000, ImS( 1) = - 1.094304;( 2) = - 1.950000, ImS( 2) = - 1.094304. Координаты точек переходного процесса приведены в таблице 4.6 Таблица 4.6 - Координаты точек вспомогательной кривой
Переходные кривые моделей показаны на рисунке 4.7. |
0,1 Плотность: 
0,5
: 3 
: 43550