математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Московский финансово-промышленный университет «Синергия» Кафедра Информационных систем и технологий Прокимнов Н.Н. Handbook по дисциплине «Математическое моделирование» Программа магистерской подготовки Москва 2014 Содержание F(0, 02, ... , вп) = P(Ti <01, 7*2 <^2, ... , 7 <вп) , 21 tk = k \ k , k = 1,2,...,6 28 fT ' 29 у2 _ У1 (f к - fk) 29 Лнабл / , rT ' 29 Pk =^p0,k = 1,2- n 84 л — — — — — — 84 — 84 Проверка графа модели. 196 Вопросы для самопроверки: 197 Литература по теме: 197 Вопрос 2. Узловые операторы. 201 Вопрос 3. Текст программной модели СМО. 202 Вопрос 4. Сборка и запуск исполнительного модуля модели. 205 File \cnv-> Projects -> Win32 Application. 206 • Build Execute ModelPro.exe. 207 Вопрос 5. Результаты моделирования. 208 Вопросы для самопроверки: 211 3.Какую функцию выполняет предложение #include ? 211 term? 211 Литература по теме: 211 Вопрос 2. Использование узла parent. 215 Вопрос 3. Использование узлов pay, rent, down. 216 Вопрос 4. Многослойная модель бизнес-процесса. 219 Выводы: 225 Вопросы для самопроверки: 226 Литература по теме: 226 Вопрос 2. Определение нестандартных выходных параметров. 230 Вопрос 3. Отладка модели. 233 Вопрос 4. Построение гистограмм. 235 Вопросы для самопроверки: 240 Литература по теме: 240 Вопрос 2. Отсеивающий эксперимент 246 F"=! F 249 Вопрос 33. Аналитическое описание функции отклика. 250 ■ n(n - l)(n - 2)...(n - i -1) 251 1-2 • ....i 251 , 4 • 3 • 2 251 4 1-2 • 3 251 b + bx + bx +... + bx = bx + bx + bx +... + bx =V bx 251 Вопрос 4. Поиск оптимальных значений. 253 Выводы: 254 Вопросы для самопроверки: 255 Приложение 255 Узловые операторы системы Pilgrim 255 неизвестен и задача исследователя состоит, прежде всего, в том, чтобы найти вид этого уравнения. При этом к числу варьируемых параметров х[,..., хп , относят все учитываемые внешние факторы и параметры исследуемого объекта, а к числу искомых параметров относят внутренние параметры модели px,..., pm , связывающие факторы х[,..., хп с показателем Y' наиболее правдоподобным отношением. Решением этой проблемы занимается теория планирования эксперимента, элементы которой рассматриваются в последней теме настоящего курса. Положения этой теории применительно к указанной задаче позволяют, основываясь на выборочных измерениях значений параметров х[,..., хп и показателя Y', найти параметры px,..., pm, при которых функция Y f (...- хп- pi-...- pm) - (2) наиболее точно отражает реальную закономерность Y f (Xl,..., хп- Zi-...- zr- Щ-...- ws). (1). Точность модели различна в разных условиях функционирования объекта, которые характеризуются внешними параметрами. В пространстве внешних параметров необходимо выделить область адекватности модели, где погрешность меньше заданной предельно допустимой погрешности. Определение области адекватности моделей является довольно сложной и трудоемкой задачей, решение требующей больших вычислительных и временных ресурсов, которые с увеличением размерности пространства внешних параметров растут нелинейно. Эта задача по объему может значительно превосходить задачу параметрической оптимизации самой модели, поэтому для вновь проектируемых объектов может не решаться. Универсальность модели определяется в основном числом и составом учитываемых в модели внешних и выходных параметров. Задачей разработчика модели является определение множества этих параметров таким образои, чтобы обеспечить получение нужных результатов в достаточно широкой области исследований. Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации - затратами машинного времени и памяти. Для решения достаточно сложных задач это обстоятельство может иметь очень большое значение. Противоречивость требований к модели - широкая область адекватности, высокая степень универсальности и экономичность - обусловливает необходимость создания для объектов одного и того же типа не одной модели, а некоторого их набора, в котором каждая модель предназначена для решения конкретных, в общем случае непересекающихся, задач. Степень соответствия модели своему назначению и ее практическая полезность характеризуется также наличием у нее таких свойств как: Наглядность, под которой понимается обозримость основных свойств и отношений. Управляемость, предполагающая наличие в модели хотя бы одного параметра, изменениями которого можно имитировать поведение моделируемой системы в различных условиях. Доступность и технологичность для проведения исследования или воспроизведения поведения. Адаптивность, под которой понимается способность модели приспосабливаться к различным входным параметрам и воздействиям окружения. Способность к эволюции, т.е., к количественному и качественному развитию. Выводы: 1. Решение многих научных и практических задач сопряжено с большими трудностями в силу невозможности проведения эксперимента с реальным объектом или связанных с проведением эксперимента большими затратами. Преодолеть эти трудности можно путем моделирования изучаемого объекта. Методология моделирования является универсальной как по отношению к типу изучаемых объектов и явлений, так и в смысле постановок задач исследований, которые могут выходить за границы применимости классических теорий и требовать междисциплинарного подхода. Для правильного выбора подхода к решению задач моделирования, так же как и в других областях науки необходима классификация моделей по различным признакам. Одним из наиболее распространенных классов моделей являются математические модели, дающие возможность получить во многих случаях решение с приемлемой точностью при относительно небольших затратах на построение моделей и проведение с ними экспериментов. Эффективность моделирования зависит от того, насколько полно построенная модель соответствует предъявляемым требованиям. Набор этих требований зависит от специфики решаемой задачи, однако, практически во всех случаях в число этих требований входят требования адекватности, универсальности и экономичности. Вопросы для самопроверки: Что такое модель? Что называется моделированием? Где применяются модели? В чем состоит особенность моделирования как методологии? Каковы основные преимущества моделирования? Как классифицируются модели? В чем состоят преимущества и недостатки математических моделей по сравнению с натурными моделями? Как классифицируются математические модели? Чем объясняется широкое распространение математических моделей? Какие бывают математические модели в зависимости от используемого математического аппарата? В чем заключаются отличия линейных моделей от нелинейных? Чем отличается статистическая модель от динамической? Чем отличается детерминированная модель от стохастической? Как различаются модели по критерию модельного времени? Что такое адекватность? Что такое область адекватности? Как можно обосновать адекватность на основе формального сравнения оригинала и модели? Что понимается под требованием универсальности модели? Литература по теме: Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. - М.: Маркет ДС, 2010. - 464 с. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. - М.: Финансы и статистика, 2009. - 848 с. Тема 2. Построение математических моделей Цели изучения темы: познакомиться с возможностями и аппаратом математического моделирования для решения задач анализа и проектирования сложных систем. Задачи изучения темы: познакомиться теоретическими основами моделирования; выяснить основы построения математического описания исследуемых объектов; представить основные этапы построения модели и проведение исследований на ее основе. Успешно изучив тему, Вы: получите представление о: этапах моделирования и их логической последовательности; концепциях построения математического описания; будете знать: перечень основных задач, решаемых в процессе моделирования; основные термины и понятия, применяемые для построения математического описания; шкалы, применяемые для измерения качественных и количественных применяемых в описании модели показателей. Вопросы темы: Теоретические основы математического моделирования. Измерение свойств. Шкалы измерений. Вопрос 1. Теоретические основы математического моделирования. Философскую концепцию моделирования составляют теория отражения и теория познания, а формально-методическую основу моделирования составляют теория подобия, теория эксперимента, математическая статистика, математическая логика и научные дисциплины, изучающие те предметные области, которые подлежат исследованию методами моделирования. Согласно математической теории подобия абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании большинства систем (за исключением, возможно, моделирования одних математических структур другими) абсолютное подобие невозможно, и основная цель моделирования - модель достаточно хорошо должна отображать функционирование моделируемой системы. Одними из основных понятий, используемых в моделировании, являются понятия изоморфизма и гомоморфизма. Изоморфизм и гомоморфизм (греч. isos — одинаковый, homoios — подобный и morphe — форма) — понятия, характеризующие соответствие между структурами объектов. Две системы, рассматриваемые отвлеченно от природы составляющих их элементов, являются изоморфными друг другу, если каждому элементу первой системы соответствует лишь один элемент второй и каждой связи в одной системе соответствует связь в другой и обратно. Такое взаимно-однозначное соответствие называется изоморфизм (Рис. 3). 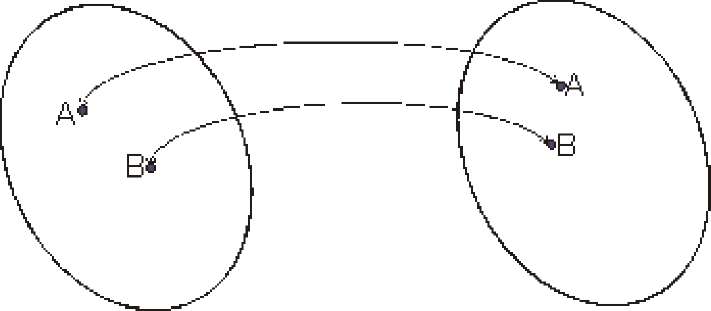 Рис. 3. К понятию изоморфизма Полный изоморфизм может быть лишь между абстрактными, идеализированными объектами, например, соответствие между геометрической фигурой и ее аналитическим выражением в виде формулы. Например, окружность может быть задана в виде формулы х2 + y2 = r2, или в виде графика в декартовой системе координат. Изоморфизм связан не со всеми, а лишь с некоторыми выбранными в процессе анализа свойствами объектов, которые в других своих отношениях могут отличаться. Гомоморфизм отличается от изоморфизма тем, что соответствие объектов однозначно лишь в одну сторону. Поэтому гомоморфный образ есть неполное, приближенное отображение структуры оригинала. Примерами гомоморфизма могут служить отношение между картой и местностью или отношение между грамзаписью и ее оригиналом. Математическая модель представляет собой некоторую абстракцию реального объекта и строится как описание последнего на основе использования основных категорий и понятий. Рассмотрим эти понятия. Под предметной областью будем понимать мысленно ограниченную область реальной действительности или область идеальных представлений, подлежащую описанию (моделированию) и исследованию. Предметная область состоит из объектов, различаемых по каким-либо признакам (свойствам) и находящихся в определенных отношениях между собой, или взаимодействующих каким-либо образом (Рис. 4). Объект
Рис. 4. К понятиям объект, свойство, показатель Под объектом понимается нечто целое, которое реально существует или возникает в нашем сознании, и обладающее свойствами, значения которых позволяют нам однозначно распознавать это целое. Объект, на котором сосредоточивается внимание субъекта с целью исследования, называется объектом исследования. Объекты воспринимаются и различаются субъектами лишь постольку, поскольку они обладают характерными свойствами. Свойством называется характерная особенность объекта, которая может быть замечена и оценена субъектом, например, вес, цвет, длина, плотность и тому подобное. Для оценки исследуемого свойства объекта субъект устанавливает определенную меру называемую показателем свойства. Для каждого показателя определяется множество значений (уровней, или градаций меры свойства), которые присваиваются ему в результате оценивания свойства. Таким образом, свойство объекта является реальностью, а показатель - субъективной мерой этой реальности (если речь идет о реальных объектах). Показатели всеобщих свойств материальных объектов, таких как пространство и время называются основными показателями. Подавляющее большинство показателей других свойств выражаются через показатели этих основных свойств. Поэтому единицы измерения основных показателей служат основой для построения стандартной системы единиц измерения физических величин и называются основными единицами измерения. Выражение показателя некоторого свойства через основные единицы измерения, принятые в определенной стандартной системе единиц (мер), называется размерностью данного показателя. Свойства делятся на внутренние (собственные) свойства объектов, показатели которых называются параметрами, и внешние, представляющие собой свойства среды, связанные некоторыми отношениями с параметрами данного объекта, показатели которых называются факторами. Свойства объектов выявляются только при их взаимодействии, или при сопоставлении объектов друг с другом. Сопоставление (комбинация) значений показателей, наблюдаемых свойств определенных объектов называется отношением. Говорят, что отношение истинно, если оно подтверждается практическим экспериментом, или логическим выводом. Отношение считается ложным, если оно опровергается практической проверкой, или логическим выводом. В противном случае отношение считается неопределенным. Понятия «истинно», «ложно», «неопределенно» являются логическими значениями любого отношения, результатами субъективной его оценки. Взаимодействие объектов определяется по результатам измерения значений показателей наблюдаемых свойств этих объектов. Поэтому каждому действию, или взаимодействию присваивается определенный результат. Это может быть значение, или определенная комбинация значений показателей свойств взаимодействующих объектов. Действия над значениями показателей свойств объектов, выполняемые по определенным правилам и приводящие к предполагаемому результату, называются операцией или процедурой. Значения показателей свойств объектов обозначаются символами из некоторого заранее определенного множества А, называемого алфавитом. Множество объектов, взаимосвязанных между собой определенными отношениями, и выполняющих определенную общую для них целевую функцию или имеющих общее предназначение, называется системой. Система, состоящая из алфавита А, строго определенных множеств отношений G, операций Q и предназначенная для символического описания объектов и систем определенного класса, называется формальной системой. Такие системы положены в основу языков математического моделирования. Энергия является одним из свойств материи, в силу которого все материальные объекты совершают движение в пространстве и времени, находясь в энергетическом взаимодействии и пространственно- временном отношении. Все материальные объекты существуют в пространстве и во времени, которые также являются всеобщими свойствами материи. Значения показателей пространства и времени входят в состав основных единиц измерения физических свойств объектов. Так как все свойства объектов изменяются во времени, то любой набор значений показателей этих свойств относится к определенному значению показателя времени. Это отношение называется состоянием объекта. Значения показателей свойств со временем меняются, в результате чего происходит смена состояний объектов. Акт смены состояний объекта, отнесенный к определенному промежутку времени, называется событием, а последовательность взаимосвязанных событий, происходящих на некотором интервале времени, называется процессом. Моделирование (в значении «метод», «модельный эксперимент») рассматривается как особая форма эксперимента, эксперимента не над самим оригиналом (это называется простым или обычным экспериментом), а над копией (заместителем) оригинала. В связи с этим одной из основных задач, решаемых в процессе исследований, является задача построения экспериментального образца, т.е., модели исследуемой системы, процесса или явления. Эта задача реализуется в идее совокупности шагов (этапов), целями которых являются сбор данных об исследуемой системе, создание содержательного описания, его формализация, разработка компьютерной программы и обоснование действующей программной модели. На созданной модели проводится изучение моделируемой системы (оригинала) путем ряда запусков программы (прогонов) на совокупности исходных данных. Собранные сведения анализируются и документируются. На рис. 5 показаны основные этапы, из которых состоит процесс моделирования. Сбор информации о моделируемом объекте С од ер ж ательн о е о пис ани е модели Разр аботка и отладка модели Оценка адекватности Экспериментальное исследование Анализ результатов моделирования До кументир ов ани е Рис. 5. Основные этапы математического моделирования Выполнение шагов описанной процедуры не является в общем случае строго последовательным: в зависимости от получаемых на одном из шагов результатов возможен возврат на предыдущие шаги с целью корректировки их результатов с последующим их повторением. Иначе говоря, процесс моделирования носит итеративный характер. Вопрос 2. Измерение свойств. Понятие измерения было известно в далекой древности, где система товарообмена основывалась на неявной шкале значений. Измерение есть представление свойств (показателей) объекта посредством номеров и чисел. Номер является материальным или квазиматериальным символом. Номера обладают свойством упорядоченности только благодаря произвольному предписанию или простой договоренности. К номерам неприменимы правила сложения и вычитания. Число является математическим понятием. Числа обладают свойством упорядоченности благодаря реальным свойствам упорядоченных объектов. В отличие от номеров к числам применимы законы сложения и вычитания. Номера так же, как и числа, упорядочены; первые — произвольные образом, вторые — на основании двух отношений, существующих между упорядоченными объектами, — отношений, специальное название которых транзитивность и антисимметричность. Транзитивность. Если А находится в некотором отношении к В, а В к С, то А находится в том же отношении к С. Симметричность. Если А находится в некотором отношения к В, то В находится в том же отношении к А. Антисимметричность. Если А больше В, то В меньше А. Отношение порядка применимо к свойству твердости: все тела, к которым применимо это понятие, связаны между собой транзитивным и антисимметричным отношением «тверже, чем» или обратным отношением «мягче, чем»; каждое тело, твердость «которого мы хотим определить, либо тверже любого другого тела того же класса, либо мягче него. Например, отношение «тверже, чем» является транзитивным и антисимметричным. Оно транзитивно потому, что если А оставляет царапину на В, а В — на С, то А оставляет царапину на С. Оно антисимметрично потому, что если А оставляет царапину на В, то В не оставляет царапину на А. Сложение — это процедура, выполняемая, как правило, над числами и над величинами, характеризующими свойства тел, например вес. Веса обладают свойством аддитивности. Если тело весом 1 соединить с другим телом того же веса, то образуется тело, вес которого равен сумме весов двух тел, т.е., 2. Можно построить приемлемую процедуру сложения весов, но не удельных весов. Однако удельный вес не обладает свойством аддитивности: нельзя построить такой процесс соединения двух тел с равным удельным весом, посредством которого было бы образовано тело с удельным весом, большим, чем удельный вес каждого из этих двух тел. Соединяя два тела с равным удельным весом, мы получаем тело с тем же самым удельным весом. Если попытаться применить сложение для удельных весов, то придем к выводу о том, что правило сложения неверно. Различие между этими двумя характеристиками связано с различием между количеством вещества и его качеством. Количество вещества в теле есть нечто такое, что увеличивается при объединении двух тел, в то время как качеством вещества являются такие признаки, которые посредством объединения двух одинаковых тел вообще не меняются. Поэтому свойства вещества, которые удовлетворяют закону сложения, являются количественной характеристикой, в то время как свойства, для которых закон сложения неверен, есть качественная характеристика вещества. Цвет является качественной характеристикой, но не количественной, поскольку: нельзя подобрать транзитивное и антисимметричное отношения, которые выражали бы различия в цвете; для цветов не существует естественной упорядоченности, которая дала бы нам возможность присвоить им номера, если не считать произвольной договоренности. Произвольной в том смысле, что эта договоренность не следует из эксперимента. Порядковый номер, соответствующий той или иной степени твердости, несет в себе определенные экспериментальные факты, чего нельзя сказать про порядковый номер цвета. Именно поэтому мы считаем, что твердость есть подлежащее измерению свойство в том смысле, в котором свойство цвета не является измеримым. Таким образом: Существует два вида свойств: количественные и качественные. Измерение применимо к обоим видам, но количественные свойства допускают измерение более высокого уровня, чем качественные. Уровень измерения свойства зависит от характеристик последнего — транзитивности, симметричности, аддитивности и т. п., что определяет выбор используеммой шкалы измерения. Вопрос 3. Шкалы измерений. Переменные различаются тем, насколько хорошо они могут быть измерены или, другими словами, как много измеряемой информации обеспечивает шкала их измерений. В каждом измерении присутствует некоторая ошибка, определяющая границы количества информации, которое можно получить в данном измерении. Другим фактором, определяющим количество информации, которое содержится в переменной, является тип шкалы, в которой проведено измерение. Различают номинальную, порядковую (ординальную), интервальную и относительную шкалы. Соответственно, имеется четыре типа переменных: номинальная; порядковая (ординальная); интервальная; относительная (отношений). Номинальная шкала. Шкала, содержащая только категории; данные в ней не могут упорядочиваться, с ними не могут быть произведены никакие арифметические действия. Номинальные переменные используются только для качественной классификации. Это означает, что данные переменные могут быть измерены только в терминах принадлежности к некоторым, существенно различным классам; при этом вы не сможете определить количество или упорядочить эти классы. Например, вы сможете сказать, что два индивидуума различимы в терминах переменной А (например, индивидуумы принадлежат к разным национальностям). Данные, измеренными в этой шкале, не могут упорядочиваться, с ними не могут быть произведены никакие арифметические действия. Номинальная шкала состоит из названий, категорий, имен для классификации и сортировки объектов или наблюдений по некоторому признаку. Для номинальной шкалы применимы только операции равно (=) и не равно (£). Часто номинальные переменные называют категориальными. Примерами могут служить профессия, город проживания, семейное положение или пол человека. Порядковая шкала. Шкала, в которой числа присваивают объектам для обозначения относительной позиции объектов, но не величины различий между ними. Эта шкала дает возможность ранжировать значения переменных. Измерения же в порядковой шкале содержат информацию только о порядке следования величин, но не позволяют сказать насколько одна величина больше другой, или насколько она меньше другой. Порядковые переменные иногда также называют ординальными. Для порядковой шкалы применимы операции равно (=), не равно (^), больше (>), меньше (<). Само расположение шкал в следующем порядке: номинальная, порядковая, интервальная является примером порядковой шкалы. Другими примерами могут служить: • место (1, 2, 3...), занятое командой на спортивном соревновании; • социальный статус семьи (можно утверждать, что верхний средний уровень выше среднего уровня, однако нельзя сказать, что разница между ними составляет, например, 30%). Интервальная шкала. Шкала, разности, между значениями которой могут быть вычислены, однако их отношения не имеют смысла. Интервальные переменные позволяют не только упорядочивать объекты измерения, но и численно выразить и сравнить различия между ними. Например, температура, измеренная в градусах Фаренгейта или Цельсия, образует интервальную шкалу. Мы можем не только сказать, что температура 40 градусов выше, чем температура 30 градусов, но и что увеличение температуры с 20 до 40 градусов вдвое больше увеличения температуры от 30 до 40 градусов. Эта шкала позволяет находить разницу между двумя величинами, обладает свойствами номинальной и порядковой шкал, а также позволяет определить количественное изменение признака. Номинальная и порядковая шкалы являются дискретными, а интервальная шкала - непрерывной, она позволяет осуществлять точные измерения признака и производить арифметические операции сложения, вычитания, умножения, деления. Для интервальной шкалы применимы операции равно (=), не равно (^), больше (>), меньше (<),сложения (+) и вычитания (-). Например, если температура воды в море утром - 19 градусов, вечером - 24, т.е. вечерняя на 5 градусов выше, то нельзя сказать, что она в 1,26 раз выше. Относительная шкала. Шкала, в которой есть определенная точка отсчета и возможны отношения между значениями шкалы. Относительные переменные очень похожи на интервальные переменные. В дополнение ко всем свойствам переменных, измеренных в интервальной шкале, их характерной чертой является наличие определенной точки абсолютного нуля, таким образом, для этих переменных являются обоснованными предложения типа: X в два раза больше, чем Y. Типичными примерами шкал отношений являются измерения времени или пространства. Например, температура по Кельвину образует шкалу отношения, и мы можем не только утверждать, что температура 200 градусов выше, чем 100 градусов, но и что она вдвое выше. Интервальные шкалы (например, шкала Цельсия) не обладают данным свойством шкалы отношения. Заметим, что в большинстве статистических процедур не делается различия между свойствами интервальных шкал и шкал отношения. Для относительной шкалы применимы операции равно (=), не равно (^), больше (>), меньше (<), сложения (+), вычитания (-), умножения (*) и деления (/). Относительные и интервальные шкалы являются числовыми. Таблица 1 и Таблица 2 поясняют использование шкал в разных задачах. Таблица 1. Использование различных шкал для сбора данных о кадровом составе
Таблица 2. Использование различных шкал для измерений погодных условий
Выводы: Методология моделирования основывается на нескольких фундаментальных философских и математических теориях. Основными понятими, используемыми в моделировании, являются понятия изоморфизма и гомоморфизма, опеределяющих отношение между объектом и моделью. Процесс построения и использования модели состоит из последовательности определенных шагов с четко выраженным результатом выполнения каждого шага. В силу сложности задачи, неполноты сведений и возможной неоднозначности логика выполнения шагов может носить итеративный характер, с возвратом на предыдущие шаги в случае получения неудовлетворительного результата, либо выявления ошибок или неточностей предыдущих шагов. Математическое описание моделируемого объекта разрабатывается на основе взаимосвязанной совокупности характеризующих объект показателей. Модель включает наиболее существенное подмножество этих показателей, которые могут относиться как к количественным, так и качественным. Для измерения показателей используются шкалы. В зависимости от типа показателей и потребностей модели для измерения показателя может выбираться та или иная шкала, позволяющая получить разный объем сведений относительно моделируемого объекта и выполнять над показателями математические операции. Вопросы для самопроверки: Какие теории образуют концептуальный базис моделирования? Что такое изоморфизм? Приведите пример. Что такое гомоморфизм? Приведите пример. Что называется свойством? На какие категории подразделяются свойства? Что такое показатель? Что понимается под отношением? Что понимается под состоянием объекта? Что такое называется событием? Что такое процесс? Назовите основные этапы процесса моделирования. Что называется номером? Что называется числом? В чем заключается различие между номером и числом? Объясните разницу между количественной и качественной характеристикой. Что представляет собой номинальная шкала? Какие операции применимы в номинальной шкале. Что представляет собой порядковая шкала? Какие операции применимы в порядковой шкале. Что представляет собой интервальная шкала? Какие операции применимы в интервальной шкале? Что представляет собой шкала отношений? Какие операции применимы в шкале отношений? Литература по теме: Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении / Под ред. А.А. Емельянова. - М.: Финансы и статистика, 2009. - 368 с. Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1968. - 356 с. Емельянов А.А., Власова Е.А., Дума Р.В., Емельянова Н.З. Компьютерная имитация экономических процессов: Учебник / Под ред. А.А. Емельянова. - М.: Маркет ДС, 2010. - 464 с. Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. - М.: Финансы и статистика, 2009. - 848 с. |
