математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205

• Название: Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
• Анкор: математическое моделирование
• Дата: 02.06.2022
• Размер: 1.51 Mb.
• Имя файла: Т 1 МАТ. Моделирование.docx
• Тип: Литература; #564707
• страница: 3 из 31

Определим интенсивность входящего потока покупателей за час работы отделения и, используя критерий Пирсона с уровнем значимости а=0,05, подвергнем проверке гипотезу о том, что поток описывается пуассоновским законом распределения.

Сгруппируем данные по числу клиентов банка к, посетивших отделение в течение часа, а результаты представим в виде таблицы:

k	1	2	3	4	5	6	7	8	9
fk	3	19	23	21	6	4	2	1	1

Предварительно заполнив в таблице для удобства вычислений дополнительную строку со значениями произведения к ■ f

k	1	2	3	4	5	6	7	8	9
fk	3	19 _|	23 _|	21 _|	6	4	2	1	1	80 _|
k x fk	3	38 _|	69 _|	84 _|	30 _|	24 _|	14 _|	8	9 |	279 J

найдем величину интенсивности потока Я

9

X к ■ fk

:=1


9

^k 279

Я = к = = ²⁷⁹ = 3,49.

⁹ 80
9


'к

к=i
X f

По формуле:

					fT Jk	лХ = N—e k!	-X
		где			N =	9 Е h = k=1	80.
		Находим и заносим в строку fj теоретические значения частот:
	k	1	2	3	4	5	6		7		8		9
	fk	3	19	23	21	6	4		2		1		1		80
	k х fk	3	38	69	84	30	24		14		8		9		279 J
	fT	8,53 J	14,88	17,29	15,08 J	10,52 J	6,11 J		3,05 J		1,33 J		0,51 J
		Вычислим и занесем в строку таблицы:
					(h - fT )2 fT .
Значения, стоящие формуле:					в числителе выражения под						знаком		суммы		в
					v2 = /ьнабл	у1 (fk - fk)2 rT ' k=1 fk
		Для наблюдаемого значения критерия Пирсона:
	k	1	2	3	4	5	6		7		8		9
	fk	3	19	23	21	6	4		2		1		1		80
	k x fk	3	38	69	84	30	24		14		8		9		279 J
	fT	8,53 J	14,88	17,29	15,08	10,52	6,11 J		3,05 J		1,33 J		0,51 J
	(fk - f	-T\ 2 k )
	fT	3,59	1,14	1,88	2,33	1,94	0,73		0,36		0,08		0,46		12,51
		В результате получаем наблюдаемое значение %1абл = 12,51.
По свободы:			заданному уровню значимости а=0,05 и							числу		степеней
						V = n-2,
						40

n - число групп в ряду (в нашем случае n=9) по таблице значений

2

критических точек % распределения находим

4 =4 (°'⁰⁵'⁷)=¹⁴'⁰⁷ •

Поскольку х1_абл < Хтабл (12,51 < 14,07) не отвергаем гипотезу о том, что входящий поток описывается пуассоновским законом распределения с интенсивностью Я =3,49 час^-1.

Вид теоретической и экспериментальной зависимостей для рассмотренного примера показан на диаграмме рис. 6: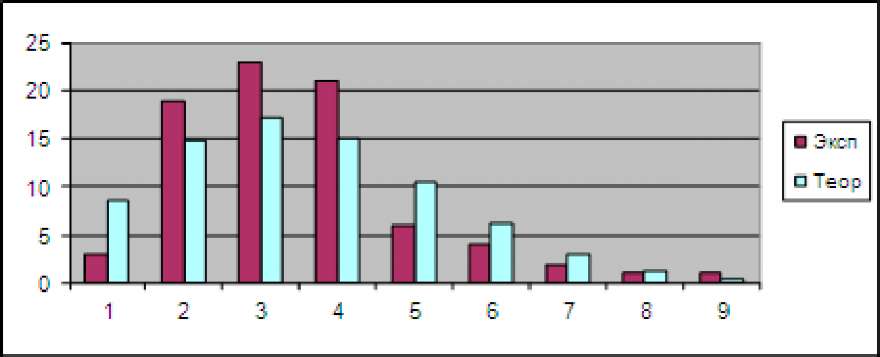




Рис. 6. Графики теоретической и экспериментальной зависимостей частот числа заявок входящего потока




Предположим теперь, что проводилось наблюдение за временем обслуживания клиентов отделения банка кассиром, в результате чего получена таблица для частот интервалов следующего вида:

	*мин	*макс	f
1	0	5	27
2	5	10	23
3	10	15	18
4	15	20	11
5	20	25	8
6	25	30	3

Определим среднее время t_s и интенсивность ц обслуживания клиентов банка, после чего обоснуем с уровнем значимости а=0,05 гипотезу о том, что время t_s распределено по экспоненциальному закону, используя для этого критерий Пирсона.

Находим среднее значение каждого временного интервала по формуле:

^min /max


Z fk/k k=1

Z f

k=1
t_k = ^k \ ^k , k = 1,2,...,6


Значения заносим в столбец, добавляемый к таблице справа:

	*мин	*макс	f	*ср
1	0	5	27	2,5
2	5	10	23	7,5
3	10	15	18	12,5
4	15	20	11	17,5
5	20	25	8	22,5
6	25	30	3	27,5

Находим среднее время ^ts




t_s = = 10,22 мин

и, предварительно подсчитав в ячейках отдельного столбца входящие в выражение для среднего времени произведения k • f

	*мин	*макс	f	tk	k • fk
1	0	5	27	2,5	67,5
2	5	10	23	7,5	173
3	10	15	18	12,5	225
4	15	20	11	17,5	193
5	20	25	8	22,5	180
6	25	30	3	27,5	82,5
Е			90

определяем интенсивность обслуживания ц:




Л=¹ =0,10мин^-1.

ts

По формуле:

rn , ...min , ...max w—»

fT _ N- ), гдеЫ = £ f _ 90

k_1

находим теоретические частоты:

	*мин	tмакс	f	tk	к • fk	fT
1	0	5	27	2,5	67,5	34,82
2	5	10	23	7,5	173	21,35
3	10	15	18	12,5	225	13,09
4	15	20	11	17,5	193	8,03
5	20	25	8	22,5	180	4,92
6	25	30	3	27,5	82,5	3,02
Е			90

Вычислим и занесем в отдельный столбец таблицы значения

(f - fT )²

fT '

входящие в выражение под знаком суммы в формуле:

у2 _ У^{1 (f} к ^{- f}k)

Лнабл / , rT '

k_1 J к

Для наблюдаемого значения критерия Пирсона:

	*мин	*макс	f	*ср	fT	(fk - fkT )2 fT
1	0	5	27	2,5	67,5	34,82
2	5	10	23	7,5	173	21,35
3	10	15	18	12,5	225	13,09
4	15	20	11	17,5	193	8,03
5	20	25	8	22,5	180	4,92
6	25	30	3	27,5	82,5	3,02
Е			90			6,75

В результате получаем %1_абл _ 6,75.

По заданному уравнению значимости а=0,05 и числу степеней свободы:

n - число групп в ряду (в нашем случае n=6) в таблице значений критических точек %² распределения, находим.

4 =4 (°'⁰⁵'⁴)=⁹'⁴⁹

Поскольку ^^ < ^_абл (6,75 < 9,49) не отвергаем гипотезу о том, что время обслуживания клиентов описывается экспоненциальным

законом распределения с интенсивностью ^=0,10мин^-1.

Вид теоретической и экспериментальной зависимостей для рассмотренного примера показан на диаграмме рис. 7: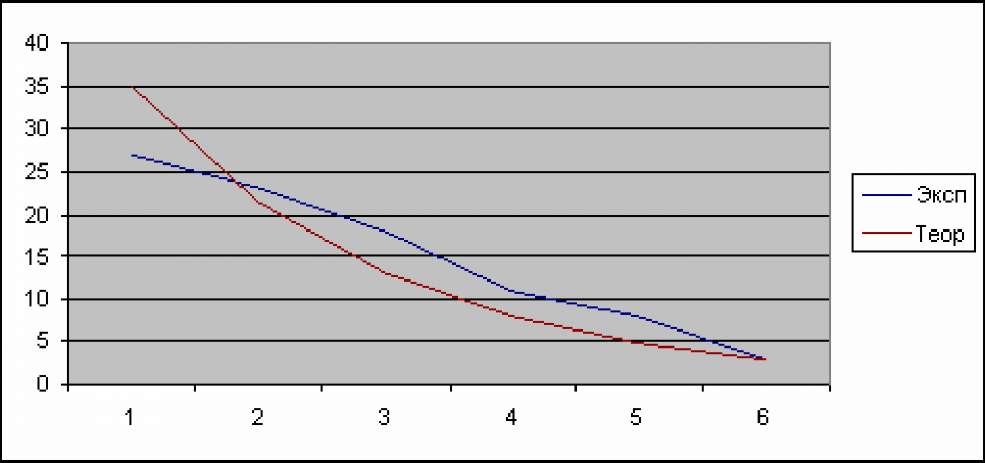




Рис. 7. Графики теоретической и экспериментальной зависимостей частот продолжительности обслуживания заявки




Выводы:

1. 
   Для эффективного решения задач на этапах сбора исходных данных для моделирования и анализа полученных результатов необходимо применять специальные методы. Одним из наиболее распространенных методов описания входных и выходных показателей является метод оценивания статистических гипотез.
   
2. 
   Существуют несколько критериев, которые могут применяться для проверки гипотез. Выбор конкретного критерия зависит от условий, в которых производится оценивание гипотезы, в первую очередь, от объема выборки используемых для оценивания данных.
   
3. 
   Для моделирования широкого класса систем и процессов необходимо строить математическое описание циркулирующих потоков объектов различного класса (информационных, материальных). Потоки
   

могут характеризоваться различными свойствами, которые обусловливают тот или иной вид их математического описания.

4. Важным частным случаем потоков в моделируемых системах и процессах является пуассоновский поток. Поэтому в практических задачах целесообразно подвергать проверке гипотезу о принадлежности наблюдаемого потока к пуассоновскому, применяя тот или иной критерий.

Вопросы для самопроверки:

1. 
   В чем состоит сущность проверки статистических гипотез, и для каких задач моделирования она применяется?
   
2. 
   Какие критерии проверки гипотез вы знаете?
   
3. 
   От чего зависит выбор того или иного критерия проверки гипотез?
   
4. 
   Что такое пуассоновский поток?
   
5. 
   Как записывается и что позволяет найти формула Пуассона?
   
6. 
   Как называется и что означает параметр пуассоновского закона?
   
7. 
   Какому закону распределения подчиняются интервалы между поступлением отдельных заявок потока?
   
8. 
   Как найти вероятность того, что в течение определенного интервала поступит не более определенного числа требований?
   
9. 
   Чему равно математическое ожидание интервала времени между событиями в пуассоновском потоке?
   
10. 
    Чему равно среднеквадратическое отклонение интервала времени между событиями в пуассоновском потоке?
    
11. 
    Для чего нужно аппроксимировать экспериментальные данные относительно потока заявок и времени обслуживания в системе массового обслуживания теоретическими зависимостями?
    
12. 
    Какие шаги нужно выполнить, чтобы построить теоретическую зависимость?
    
13. 
    Зачем нужно проводить оценку статистической значимости результата?
    

Литература по теме:

1. 
   Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1968. - 356 с.
   
2. 
   Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. - М.: Финансы и статистика, 2009. - 480 с.
   
3. 
   Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. - М.: Финансы и статистика, 2009. - 848 с.