математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Цели изучения темы: познакомиться с основными аналитическими моделями систем массового обслуживания. Задачи изучения темы: научиться применять математический аппарат описания марковских процессов к построению моделей систем массового обслуживания; познакомиться с основными показателями, используемыми в моделях систем массового обслуживания. Успешно изучив тему, Вы: получите представление о: как строятся математические модели систем массового обслуживания на примере системы с отказами; как применяются модели систем массового обслуживания; будете знать: как характеризуется пропускная способность систем с отказами и как они рассчитываются; какие показатели характеризуют очередь в системе с ожиданием и как они рассчитываются; как применить модели к решению экономических и инженерных задач. Вопросы темы: Система массового обслуживания. Моделирование одноканальной СМО с отказами. Оптимизация показателей многоканальной СМО с отказами. Обслуживание с очередями. Многоканальная СМО сограниченной очередью. Вопрос 1. Система массового обслуживания. Значительный интерес для практики представляют модели систем массового обслуживания (СМО), к которым сводятся множество задач анализа и проектирования информационных систем. Системы этого класса характеризуются наличием (рис. 15) потока запросов (заявок), поступающих на вход системы (входящим потоком), необязательной очереди ждущих обслуживания заявок, обслуживающим прибором, или каналом и потоком обслуженных заявок (выходящим потоком). |
| 1 , | Обслуживающий прибор | Выходящий ^ |
| 1 5 | поток |
Очередь
Рис. 15. Элементы СМО
Поток заявок (другие названия: запросы, вызовы, требования и т.д.), исходящий из источника заявок, поступает на вход СМО в случайные моменты времени для обслуживания. Этот входной поток может представлять собой вызовы от абонентов, передаваемые сообщения и т.д. Обслуживание поступившей заявки продолжается некоторое случайное время, после чего канал освобождается и готов к принятию следующей заявки. Случайный характер потока заявок приводит к тому, что в какие-то промежутки времени на входе СМО скапливается излишне большое число заявок (они либо образуют очередь, либо покидают СМО не обслуженными); в другие же периоды СМО будет работать с недогрузкой или простаивать.
Для СМО в рамках теории массового обслуживания разработаны математические модели, которые широко применяются для количественного оценивания системных показателей. Многие модели основаны на уже рассмотренном ранее аппарате марковских процессов. Проиллюстрируем применение теории на нескольких моделях СМО.
Вопрос 2. Моделирование одноканальной СМО с отказами.
Входящий
Вероятности состояний системы p (вероятность того, что в системе находится 0 заявок) и p (вероятность того, что в системе
Примером одноканальной СМО с отказами, которая является простейшей из моделей, может служить телефонное справочное бюро. В случае незанятой линии происходит соединение с оператором, и абонент получает ответ на заданный вопрос, в противном случае соединение не устанавливается и звонок необходимо повторить. Считая интервалы между звонками и продолжительность разговора случайными величинами, распределенными по экспоненциальному закону, процесс в такой системе можно рассматривать как марковский. Обозначив через Л интенсивность входящего потока, / - интенсивность обслуживания, можно построить размеченный ГСП (рис. 16Рис.) .
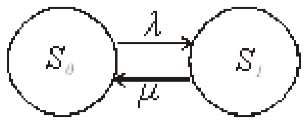
Рис. 16. ГСП одноканальной СМО с отказами
находится 1 заявка) для стационарного режима определяются из выражений для вероятностей состояний процесса гибели и размножения, который был рассмотрен в предшествующей теме:
И
Po =
1 + И
P1 =
1 1 + И
Из этих выражений можно определить показатели одноканальной СМО. В частности, вероятность отказа в обслуживании pomK:
Porn^, = P1 = Г (1) 1 + И
поскольку запрос получает отказ в случае, когда обслуживающий прибор занят, и относительную пропускную способность q, которая представляет собой отношение среднего числа обслуженных заявок за единицу времени к среднему числу всех поступивших заявок за тоже время:
q = Po = 7— (2) 1 + и
Поскольку p0 есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена.
Знаяq легко найти абсолютную пропускная способность А,
которая определяется как среднее число заявок, которое может обслужить СМО в единицу времени. Эти показатели связаны очевидным соотношением
A = 1- q (3)
Вопрос 3. Оптимизация показателей многоканальной СМО с отказами.
В многоканальной СМО имеется n каналов обслуживания, которые функционируют независимо друг от друга. Очередь отсутствует, т.е., заявки, заставшие все каналы занятыми обслуживанием, получают отказ, и уходят из системы. Входной поток заявок и поток обслуживания
заявок являются пуассоновскими. Интенсивность поступления заявок равна Я, интенсивность обслуживания /.
СМО может находиться в следующих состояниях:
S0 - в СМО 0 заявок (все каналы свободны);
S1 - в СМО 1 заявка (один канал занят, остальные свободны);
Sk - в СМО n заявок (k каналов заняты, остальные свободны);
Sn - в СМО n заявок (все каналы заняты).
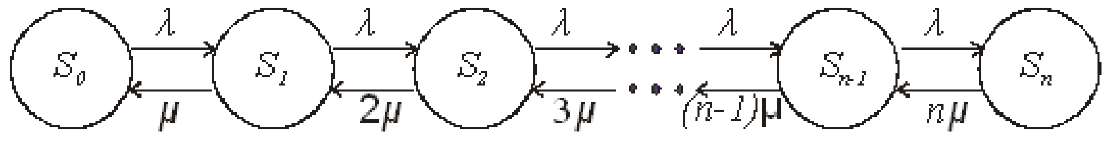
Рис. 171. ГСП многоканальной СМО с отказами
Если система находится в состоянии S1, то поток, переводящий
систему в состояние S0, будет иметь интенсивность
Если система находится в состоянии S2, то поток, переводящий
систему в состояние S1, будет иметь интенсивность 2/. (два канала
порождают поток с интенсивностью в два раза большей).
Если система находится в состоянии Sk, то поток, переводящий
систему в состояние Sk-1, будет иметь интенсивность k/. (k каналов порождают поток с интенсивностью в k раз большей).
Процесс, показанный на рис. 17, представляет собой частный случай процесса гибели и размножения.
dP0(t) dt
Уравнения Колмогорова для вероятностей состояний системыP0 , P1, ..., Pn будут иметь следующий вид:
-Ip0(t) + /P1(t)
dPk(t) dt
(4)
-X
dPn (t) dt
Предельные вероятности имеют вид
= M-1(t) - (Я + k/) Pk (t) + /(k +1) Pk+1(t)
= ^Pn-1(t) /nPn (t)
1 n P p1 p\-1
P
П!
0 - irnr -(1 + 77 + ^7 + ••• + t-r)
1! 2!
h k!
PkPo
(5)
Pk -
0, k -1,... n
k!
_ A где p- M
Pk-Sp, k - 1,...n Соотношения k! (5) называются
формулами Эрланга. С их помощью можно найти предельные вероятности в зависимости от значений параметров X и Характеристики стационарного режима таковы.
Вероятность отказа. Заявка получает отказ, если все каналы заняты. Вероятность этого равна:
n
P - P - — P (6)
отк n | 0 V /
n!
Относительная пропускная способность есть вероятность того, что заявка будет принята к обслуживанию и может быть найдена как дополнение Р до 1:
q -1 - Р (7)
отк
Абсолютная пропускная способность находится как
A-Aq-2(1 - Pn) (8)
