Лабораторная работа 1 Имитационное моделирование систем массового обслуживания
 Скачать 435.88 Kb.
|
|
Лабораторная работа 1 Имитационное моделирование систем массового обслуживания В разных областях техники, в организации производства, в экономике и медицине, в социальной сфере, в военном деле и во многих других сферах человеческой деятельности постоянно возникает необходимость решения вероятностных задач, связанных с работой систем массового обслуживания (СМО). Многообразие приложений теории массового обслуживания определяет постоянно растущий интерес к ней, а сложность возникающих задач не позволяет получить исчерпывающие решения на базе аналитических методов. В таких ситуациях часто прибегают к имитационному моделированию. Для имитации подобных систем предназначен язык моделирования GPSS, а также создаются сложные программные системы (ObjectSim, Pigrim), позволяющие реализовать модели систем массового обслуживания с помощью развитой CASE-оболочки путем выбора и связи различных строительных блоков. Различают два основных подхода к моделированию СМО: ориентированный на события и ориентированный на процессы. Событийный подход имеет преимущества в отношении гибкости и эффективности вычислений, однако менее подходит для обучения, поскольку скрывает ≪жизненный цикл≫ заявок и является менее понятным на интуитивном уровне. Кроме того, для его реализации требуется управляющая событиями подпрограмма, что приводит к необходимости использования внутреннего языка VBA. Рассмотренные ниже модели будут реализованы с использованием процессно-ориентированного подхода. Рассмотрим структуру СМО. Каждая СМО состоит из определенного числа обслуживающих единиц, которые называются каналами обслуживания. На вход СМО поступает поток требований (заявок). Таким образом, различают следующие элементы СМО: 1. входной поток заявок; 2. очередь; 3. узел обслуживания; 4. выходной поток. На рис. 1.1 указаны эти элементы для следующей СМО: бензоколонка занимается заправкой автомобилей. 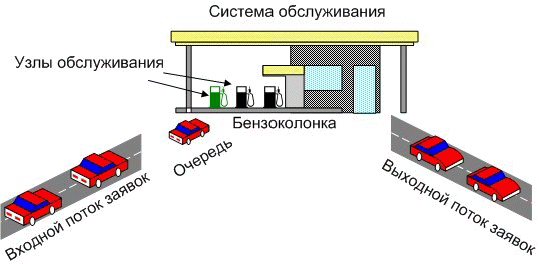 Рис. 1.1 –Пример системы массового обслуживания Входной поток заявок может быть случайным или детерминированным. В первом случае время между поступлением двух заявок является случайной величиной, а во втором –величиной детерминированной (поступление происходит в соответствие с определенным графиком). Интенсивность потока l – частота появления событий, поступающих в СМО в единицу времени. В СМО может поступать несколько входных потоков, имеющих различные характеристики (интервал поступления, приоритет и т.д.). Очередь – место, где поступившие заявки ждут начала обслуживания. В том случае, если элемент очередь в системе отсутствует, то данная система без ожидания. Это означает, что в том случае, если в момент поступления заявки все каналы обслуживания заняты, то эта заявка покидает систему необслуженной. Очередь может иметь ограниченную или неограниченную длину. Кроме того, время ожидания в очереди может быть ограничено (говорят, что рассматриваются нетерпеливые заявки). Следующая характеристика очереди – дисциплина очереди. Она связана с правилом, в соответствии с которым обслуживаются клиенты. Различают следующие дисциплины: первый пришел – первый ушел, первый пришел – последний ушел, а также существуют дисциплины с приоритетами. Рассмотрим теперь характеристики средств обслуживания. Системы обслуживания характеризуются по числу каналов обслуживания (например, если на рис. 1.1 машины могут быть обслужены несколькими устройствами, то система будет многоканальной), числу фаз обслуживания. Время обслуживание может быть случайной величиной или детерминированным. Также существуют системы, в которых обслуженные требования после некоторой задержки опять поступают на вход. Такие системы называются замкнутыми. В качестве показателей эффективности СМО рассматриваются: среднее время, которое клиент проводит в очереди, средняя длина очереди, среднее время, которое клиент проводит в системе обслуживания (  , где TotalTimeSystem - общее время пребывания в системе для всех заявок, а N -число заявок), среднее число клиентов в системе обслуживания, вероятность того, что система окажется свободной и т.д.1.1 Одноканальная система массового обслуживания Рассмотрим простую систему массового обслуживания: число каналов равно единице, время ожидания неограниченно, время между заявками и время обслуживания заявок являются случайными величинами с показательным законом распределения (среднее значение времени обслуживания равно to , среднее время между заявками - tz ) (рис.1.2). 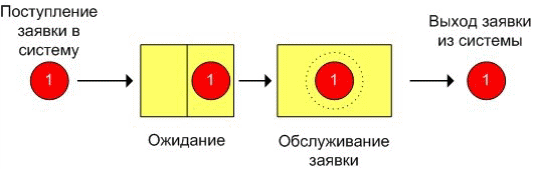 Рис. 1.2 – Одноканальная система массового обслуживания Рассмотрим процесс поступления десяти заявок, если tz =0,5 ч., to =1 ч. Можно использовать следующий способ моделирования такой системы (рис.1.3). 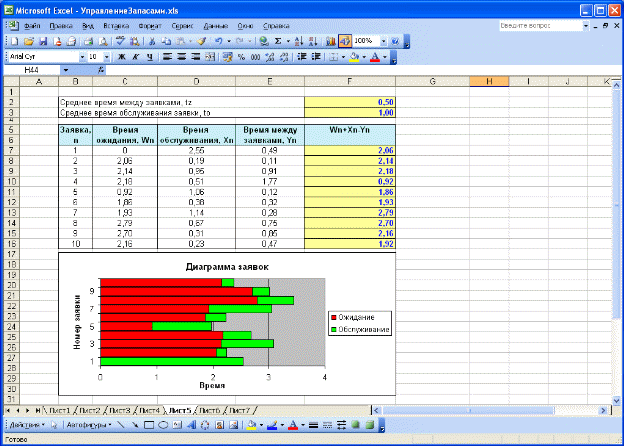 Рис. 1.3 – Результаты моделирования одноканальной СМО при tz =0,5 ч., to =1 ч. Величины времени обслуживания и между заявками рассчитываются согласно способу моделирования случайной величины с показательным законом распределения D7= –$F$3*LN(СЛЧИС()) E7= –$F$2*LN(СЛЧИС()). В последнем столбце рассчитывается величина Wn + Xn -Yn F7=C7+D7–E7. Если ее значение является отрицательным, то это означает, что следующая заявка поступит после того, как будет обслужена текущая и потому время ее ожидания будет равно нулю, а в противном случае, время ожидания составит Wn + Xn -Yn С8=ЕСЛИ(F7>0;F7;0). Изменим исходные данные ( tz =1 ч., to =0,5 ч.). Из рис. 4.4 можно увидеть, что в этом случае уменьшится время ожидания обслуживания. 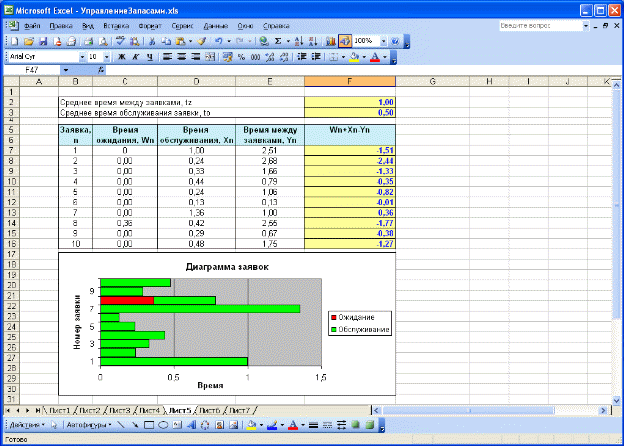 Рис. 1.4 – Результаты моделирования одноканальной СМО при tz =1 ч., to =0,5 ч. Теперь выполним моделирование, учитывая начальное время tn . Пусть tz =8 мин., to =7 мин.; tn =9 ч. Рассмотрим процесс поступления семи заявок (рис. 1.5). Определение времени между заявками и времени обслуживания (мин.) остается без изменения. Для того чтобы перевести эти значения в используемый формат времени необходимо осуществить следующие операции F8=E8/1440 D8=D7+C8/1440. Т.е. время поступления очередной заявки равно сумме времени прибытия предыдущей и случайной величины, распределенной по показательному закону. 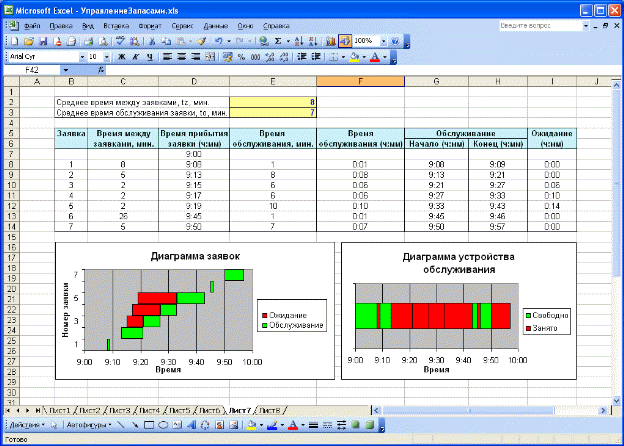 Рис. 1.5 – Моделирование одноканальной СМО с учетом начального времени Время начала обслуживания первой поступившей заявки равно времени ее поступлению G8=D8. Начиная со второй заявки, эта величина будет определяться как максимальное значение из момента окончания обслуживания предыдущей заявки и времени поступления текущей G9=ЕСЛИ(D9>=H8;D9;H8). Время окончания обслуживания рассчитывается по формуле H8=G8+F8. Период ожидания равен разности времени начала обслуживания и времени поступления I8=G8-D8. Также встречаются системы, в которых новая заявка может поступить только после того, как была обслужена предыдущая. В качестве примера, можно назвать систему, которая периодически может выходить из строя и требовать ремонта (ее отказы в данном случае рассматриваются как заявки): время между ее отказами и время обслуживания распределено по показательному закону. Очевидно, что не может произойти выход из строя системы прежде, чем будет выполнен ремонт предыдущего отказа. Такие заявки будем называть не перекрывающимися. Для того чтобы выполнить моделирование данной СМО необходимо изменить только расчет времени прибытия заявки, которое будет равно сумме момента окончания обслуживания предыдущей заявки и случайной величины, распределенной по показательному закону D9=H8+C9/1440. Результаты моделирования представлены на рис.1.6 ( tz =5 мин., to =6 мин.). 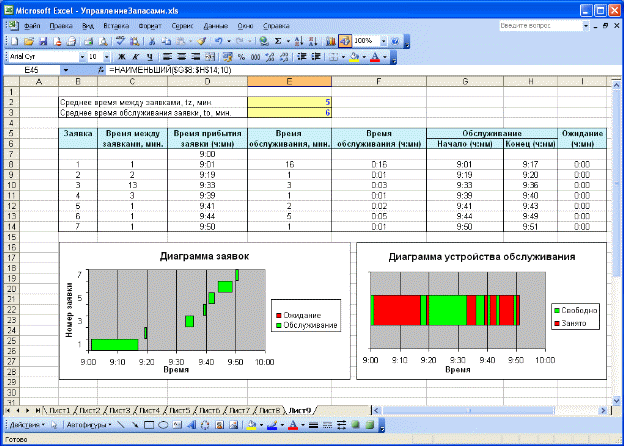 Рис. 1.6 – Моделирование одноканальной СМО с не перекрывающимися Можно заметить, что в Диаграмме заявок теперь отсутствуют периоды ожидания обслуживания. Задание 1. Выполните имитацию работы банка, осуществляющего прием вкладов. Размер депозита является случайной величиной с нормальным законом распределения (среднее значение -MD ; среднее квадратическое отклонение - SD ). Время между приходом двух вкладчиков – случайная величина с показательным законом распределения (среднее значение - tz ), а время обслуживания равномерно распределено на интервале [ a ; b ]. Пусть исходные значения равны величинам: MD =30000 руб.; SD =10000 руб.; tz =1 час; a =20 мин.; b =30 мин.; tn =9 ч., число заявок равно 5. Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлена) после прихода пяти клиентов; б) к моменту времени 12:00 ч.?  Рис. 1.7 – Система массового обслуживания ≪Банк≫ 2. Проведите 10 экспериментов и рассчитайте величины: - среднее время ожидания; - среднее число обслуженных заявок за период с 9:00 до 15:00 ч. 3. Предположите, что tn =0 и выполните имитацию описанным на рис. 1.3 способом. 4. Пусть банковская автоматизированная система может выходить из строя, что приводит к необходимости вызова специалистов, устраняющих неполадку. Выполните имитацию периодов нормальной работы системы и ее ремонта, если данные величины являются случайными с показательным законом распределения, а tz =30 дней, to =3 ч. Рассмотрите процесс поступления 5 заявок (отказов). |