МАТЕМАТИКА Практические работы №12-13. Практическая работа 12. Решение задач с реальными дискретными случайными величинами

• Название: Практическая работа 12. Решение задач с реальными дискретными случайными величинами
• Дата: 10.06.2022
• Размер: 39.97 Kb.
• Имя файла: МАТЕМАТИКА Практические работы №12-13.docx
• Тип: Практическая работа; #584568

УРОК 5.2.2

ТЕМА 5.2. СЛУЧАЙНАЯ ВЕЛИЧИНА, ЕЕ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Практическая работа №12. Решение задач с реальными дискретными случайными величинами
Цель работы: Нахождение закона распределения, функции распределения и числовых характеристик дискретной случайной величины.

Содержание работы:

Основные понятия.

1. 
   Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
   
2. 
   Дискретной случайной величиной (ДСВ) называют такую величину, множество значений которой либо конечное, либо бесконечное, но счетное.
   
3. 
   Заданное соответствие между возможными значениями СВ и их вероятностями называется законом распределения случайной величины; его можно задать таблично, аналитически (в виде формулы) и графически.
   
4. 
   При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности. Эта таблица называется рядом распределения.
   
5. 
   Ряд распределения можно представить графически, если по оси абсцисс отложить возможные значения ДСВ, а по оси ординат - соответствующие вероятности. Соединив полученные точки отрезками, получим ломаную, называемую многоугольником распределения вероятностей
   
6. 
   Функцией распределения случайной величины Х (обозначается F(x)) называется функция, определяемая соотношением F(x) = P(X < x).
   
7. 
   Математическое ожидание ДСВ Х равно сумме произведений всех ее возможных значений на их вероятности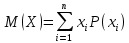
   

8. 
   Дисперсией ДСВ Х (D (X)) называют математическое ожидание квадрата отклонения СВ от ее математического ожидания, т.е.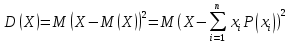
   

9. 
   Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т.е.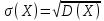
   

Пример выполнения:
Исходные данные:
Приживаемость саженцев яблонь составляет 80%. Наудачу выбирают 5 саженцев. Составить закон распределения числа прижившихся саженцев, функцию распределения, построить многоугольник распределения и график функции распределения. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа прижившихся саженцев.
Решение:

1. 
   Вероятность приживаемости яблони равна 0,8.
   

• 
  – случайная величина числа прижившихся яблонь из пяти саженцев: Возможные значения: х₁ = 0 – ни один саженец не прижился;
  

х₂= 1–один саженец прижился;

х₃= 2–два прижились;

х₄= 3–три;

х₅= 4–четыре;

х₆= 5–пять саженцев прижились.

2. 
   Вероятности этих значений вычислим по формуле Бернулли: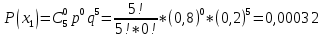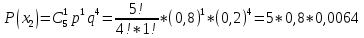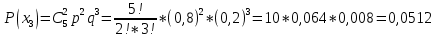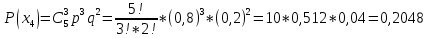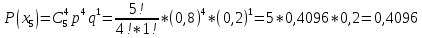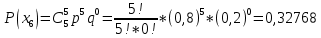
   

Таким образом, закон распределения случайной величины:

Х	0	1	2	3	4	5
Р(Х)	0,00032	0,0064	0,0512	0,2048	0,4096	0,32768

Полигон распределения выглядит следующим образом: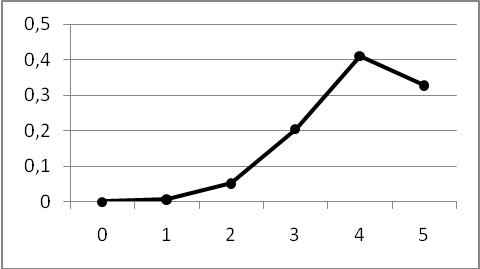



Вычислим функцию распределения: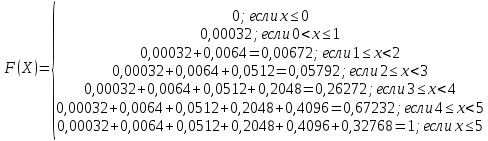



Найдем числовые характеристики случайной величины, для этого составим таблицу:

Х	0	1	2	3	4	5
Р(Х)	0,00032	0,0064	0,0512	0,2048	0,4096	0,32768
Х-М(Х)	-4	-3	-2	-1	0	1
(Х-М(Х))2	16	9	4	1	0	1

Математическое ожидание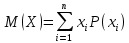

=10,0064  2 0,051230,2048  4 0,4096 50,32768  4
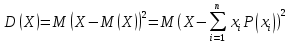Дисперсия: =160.00032 9 0,0064  4 0,0512 10,2048  0 0,4096 10,32768  0,8
Среднее квадратическое отклонение: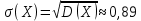
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. 
   В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны 2 детали. Составить закон распределения числа стандартных деталей среди отобранных. Найти функцию распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение. Построить полигон полученного распределения.
   

2. 
   Устройство состоит из трех независимо работающих элементов. Вероят-ность отказа каждого элемента в одном опыте равна 0,1. Составить закон распреде-ления числа отказавших элементов в одном опыте. Построить полигон полученного распределения. Найти функцию распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение
   

3. 
   Вероятность того, что стрелок попадет в мишень при одном выстреле, равна 0,7. Стрелок делает выстрелы до первого промаха. Составить закон распределения случайной величины Х – числа патронов, выданных стрелку, если всего имеется пять патронов. Построить полигон полученного распределения. Найти функцию распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение.
   

4. 
   Определить закон, функцию распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение числа гербов при четырех подбрасываниях монеты. Построить полигон полученного распределения.
   

5. 
   Два носка выбираются случайным образом из ящика, в котором находится 5 коричневых и 3 зеленых. Определить закон, функцию распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение числа коричневых носков. Построить полигон полученного распределения.