Главная страница
Навигация по странице:

  • 4) ковариацию и коэффициент корреляции. Зависимы ли случайные величины X и Y

    		•

    Типовой расчет по ТВиМС. Типовой расчет ТВи МС. Задача Закон распределения случайного вектора z (X, Y) задан таблицей. Найти


    Скачать 42.7 Kb.
    НазваниеЗадача Закон распределения случайного вектора z (X, Y) задан таблицей. Найти
    АнкорТиповой расчет по ТВиМС
    Дата27.12.2020
    Размер42.7 Kb.
    Формат файлаdocx
    Имя файлаТиповой расчет ТВи МС.docx
    ТипЗадача
    #164725



    ВАРИАНТ 2

    Задача 1. Дискретная случайная величина задана таблицей



    Найти функцию распределения случайной величины, построить ее график, найти математическое ожидание, дисперсию, стандартное отклонение.

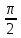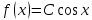    Задача 2. Случайная величина X в интервале (0, ) задана плотностью распределения вероятностей , а вне этого интервала f(x)= 0. Найти C, функцию распределения вероятностей случайной величины X , ее математическое ожидание, дисперсию, стандартное отклонение.

    Задача 3.

    Закон распределения случайного вектора Z = (X, Y) задан таблицей. Найти:

    1) законы распределения случайных величин X и Y;

    2) математическое ожидание MZ;

    3) дисперсии DX и DY;


    4) ковариацию и коэффициент корреляции. Зависимы ли случайные величины X и Y?

    5) уравнение регрессии Х на Y и Y на Х;

    6) закон распределения случайной величины X при условии, что Y принимает

    любое из всех возможных для нее значений.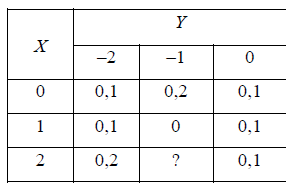


    1)

    a) Находим математическое ожидание:

    M(X) = ∑x(i)*p(i) = -7*0,2-3*0,15+1*0,2+3*0.2+12*0,15+23*0,1 = 3,05

    б) Находим дисперсию:

    D(X) = M(X²) - [M(X)]²

    M(X²) =∑x²(i)*p(i)= 49*0,2+9*0,15+1*0,2+9*0.2+144*0,15+529*0,1 = 87,65

    [M(X)]² = (3,05)² = 9.3025

    D(X) = 87,65 – 9.3025 = 78,3475

    в) Находим стандартное отклонение:

    σ(X) = √D(X) = √78,3475 ≈ 8,85

    Составим функцию распределения:

    F(x)=P(X
    1. F(x)=P(X<-7)=0

    2. F(x)=P(X<-3)=P(X=-7)=0,2

    3. F(x)=P(X<1)=P(X=-7)+P(X=-3)=0,2+0,15=0,35

    4. F(x)=P(X<3)=P(X=-7)+P(X=-3)+P(X=1)=0,2+0,15+0,35=0,7

    5. F(x)=P(X<12)=P(X=-7)+P(X=-3)+P(X=1)+P(X=3)= 0,2+0,15+0,35+0,7=1,4

    6. F(x)=P(X<23)=P(X=-7)+P(X=-3)+P(X=1)+P(X=3)+P(X=12)= 2.8

    7. F(x)=P(X>23)=2,8+0,1=2,9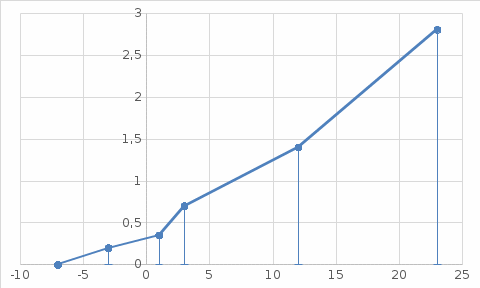



    2)

    Пусть случайная величина X задана плотностью вероятности:

    0, x<0

    f(x) = C cosX, 0=π/2

    0, x>π/2

    Определим из условия нормировки:





    Cледовательно, C =1, а функция распределения случайной величины X имеет вид:

    0, x<0

    F(x)= sinx, 0=π/2

    0, x>π/2

    Вычислим математическое ожидание случайной величины X: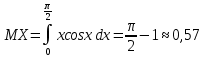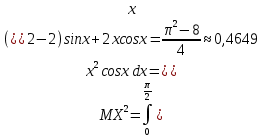





    Вычислим дисперсию случайной величины X: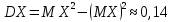



    Cтандартное (среднеквадратическое) отклонение:



    3)

    А) Случайная величина Х может принимать значения:

    Х=0 с вероятностью p1 = 0.1+0.2+0.1=0.4

    X=1 с вероятностью p2 = 0.1+0+0.1=0.2

    X=2 с вероятностью p3 = 0.2+0.1+0.1=0.4

    Случайная величина Y может принимать значения:

    Y=0 с вероятностью p1 = 0.1+0.1+0.2=0.4

    Y=1 с вероятностью p2 = 0.2+0+0.1=0.3

    Y=2 с вероятностью p3 = 0.1+0.1+0.1=0.3

    Б) Находим ряды распределения X и Y.

    Х 0 1 2

    P 0.4 0.2 0.4

    Математическое ожидание M[X]:

    M(X)=0*0.4+1*0.2+2*0.4=1

    Y -2 -1 0

    P 0.4 0.3 0.3

    Математическое ожидание M[Y]:

    M(Y)=-2*0.4-1*0.3+0*0.3=-1.1

    M(X+Y)=1-1.1=-0.1

    M(XY)=0.1*1*(-2)+0.2*2*(-2)+0.1*2*(-1)=-0.2-0.8-0.2=-1.2

    В) D(X) = 1*0.2+4*0.4-(1*0.2+2*0.4)^2=1.8-1=0.8

    D(Y)=4*0.4+1*0.3-(-2*0.4-1*0.3)^2=1.9-1.21=0.69

    Г) cov(X,Y)=-1.2-1*(-1.1)=-0.1

    r(XY)=-0.1/(0.894*0.831)=-0.135 (отрицательная корреляционная зависимость)

    Д)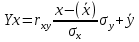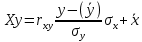


    написать администратору сайта