теория массового обслуживания. Ответы ТМО. Экзаменационный билет 25

• Название: Экзаменационный билет 25
• Анкор: теория массового обслуживания
• Дата: 04.05.2022
• Размер: 255.25 Kb.
• Имя файла: Ответы ТМО.docx
• Тип: Программа; #511960

Карагандинский технический университет

Экзаменационный билет № 25

Кафедра Информационные технологии и безопасность

Дисциплина «Теория массового обслуживания»

Образовательная программа 6В06301– Системы информационной безопасности
1. Классификация и структура систем массового обслуживания.

СМО классифицируются по следующим признакам:

1) число фаз обслуживания:

– однофазовые;

– многофазовые.

2) число каналов обслуживания: – одноканальные;

– многоканальные. В свою очередь подразделяются на:

– полнодоступные – имеющие однородные (с одинаковыми характеристиками) каналы;

– неполнодоступные – имеющие неоднородные каналы.

3) тип входящего потока требований:

– с простейшим (пуассоновским) потоком;

– с входящим потоком иного типа.

4) вероятностные характеристики времени обслуживания:

– со случайным временем обслуживания;

– с фиксированным постоянным временем обслуживания.

5) характер случайного процесса, происходящего в СМО:

– Марковские – СМО, в которых входящий поток требований является пуассоновским и время обслуживания подчинено показательному закону (позволяют легко описать и построить математическую модель, имеют простые решения)

– Немарковские СМО – как правило, требуют применения статистического моделирования с использованием ЭВМ.

6) наличие возможности ожидания обслуживания:

– с отказами, в которых заявка, поступившая в СМО в момент, когда все каналы заняты, получает отказ и покидает очередь;

– с ожиданием, в которых заявка становится в очередь и ждет, пока не освободится один из каналов. В свою очередь подразделяются на СМО с:

– ограниченным ожиданием. Ограничения по длине очереди или по времени ожидания в очереди;

– неограниченным ожиданием.

7) наличие приоритетов обслуживания:

– без приоритетов;

– с приоритетами.

8) наличие ограничений потока требований:

– замкнутые – СМО с ограниченным потоком требований, в которых обслуженные требования могут возвращаться в СМО;

– открытые.

2. Дайте определения Марковского процесса, Марковской цепи.

Марковский процесс – это физическая система, изменившая свое положение и состояние, которые заранее не были запрограммированы.

Цепь Маркова – череда событий, в которой каждое последующее событие зависит от предыдущего.

3. Задача. Среднее число покупателей, поступающих на узел расчета в магазине самообслуживания, 100 человек в час. Кассир может обслуживать 60 человек в час. Определите, какое число кассиров необходимо для того, чтобы вероятность появления очереди не превысила 0,60

Интенсивность потока обслуживания:



. Интенсивность нагрузки.
ρ = λ*t_обс = 100*1/60 = 1.667

Вероятность, что канал свободен (доля времени простоя каналов).


Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов).
n_з = ρ*p_обс = 1.667*0.375 = 0.625 канала.

Зав. кафедрой Коккоз М.М._________Разработал Авилова Е.К._________

Утверждено: Протокол № 16А от 28.03.2022г.

Карагандинский технический университет

Экзаменационный билет № 26

Кафедра Информационные технологии и безопасность

Дисциплина «Теория массового обслуживания»

Образовательная программа 6В06301– Системы информационной безопасности
1. В чем заключается процесс «рождения-гибели».

Процесс рождения-смерти (или процесс рождения и смерти) является частным случаем непрерывного марковского процесса, в котором переходы состояний бывают только двух типов: "рождения", которые увеличивают переменную состояния на единицу, и "смерти", которые уменьшают состояние на единицу. Название модели происходит от общего применения, использования таких моделей для представления текущей численности населения, где переходы являются буквальными рождениями и смертями.

2. Перечислите русских учёных, которые внесли значительный вклад в развитие теории массового обслуживания.

Значительный вклад в развитие теории и практики массового обслуживания внесли зарубежные ученые К. Пальм, Д. Кендалл, Т. Саати и др., а также отечественные ученые И.П. Алдохин, Н.П. Бусленко, Б.В. Гнеденко, Е.С. Вентцель, А.Я. Хинчин и др.

3. Задача. Рабочий обслуживает 4 станка, каждый станок отказывает с интенсивностью 0,5 отказа в час. Среднее время ремонта одного станка 0,8 ч. Все потоки событий простейшие. Определите основные показатели, характеризующие систему массового обслуживания.

μ =1,25

ρ =0,5:1,25

ρ=0,4.

Вероятность простоя рабочего:

Р зан=1-Р0.

Если раб. занят, он налаживает μ станков в ед. времени, проп. способность системы -

А=(1-P0)

μ=0,85μ станков в час
Зав. кафедрой Коккоз М.М._________Разработал Авилова Е.К._________

Утверждено: Протокол № 16А от 28.03.2022г.

Карагандинский технический университет

Экзаменационный билет № 27

Кафедра Информационные технологии и безопасность

Дисциплина «Теория массового обслуживания»

Образовательная программа 6В06301– Системы информационной безопасности
1. Экономико-математическая постановка задач массового обслуживания

В процессе постановки задач необходимо раскрыть взаимосвязи показателей СМО, которые по своей базовой принадлежности можно разделить на две группы: первая связана с издержками обращения С_ио, которые определяются числом занятых обслуживанием каналов, затратами на содержание СМО, интенсивностью обслуживания, степенью загрузки каналов, эффективностью их использования, пропускной способностью СМО и др.; вторая группа показателей определяется издержками собственно заявок С_ип, поступающих на обслуживание, которые образуют входящий поток, ощущают эффективность обслуживания и связаны с такими показателями, как длина очереди, время ожидания обслуживания, вероятность отказа в обслуживании, время пребывания заявки в СМО и др.

2. Многоканальная система массового обслуживания без ограничений

В системах массового обслуживания без ограничений теоретически предполагается, что очередь будет расти бесконечно, следовательно, вероятность отказа в обслуживании будет равна нулю.



3. Задача. Определите оптимальное число телефонных номеров, необходимых для установки на коммерческом предприятии, при условии, что заявки на переговоры поступают с интенсивностью 90 звонков в час, а средняя продолжительность разговора по телефону составляет 2 мин.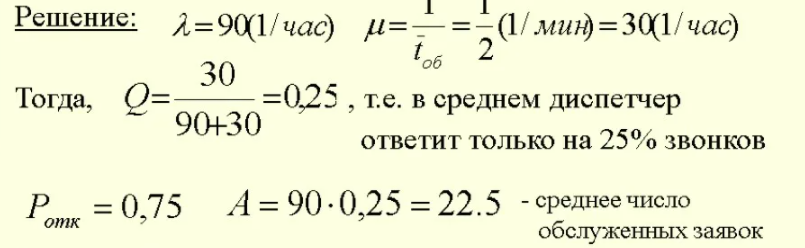



Зав. кафедрой Коккоз М.М._________Разработал Авилова Е.К._________

Утверждено: Протокол № 16А от 28.03.2022г.

Карагандинский технический университет

Экзаменационный билет № 28

Кафедра Информационные технологии и безопасность

Дисциплина «Теория массового обслуживания»

Образовательная программа 6В06301– Системы информационной безопасности
1. Одноканальная система массового обслуживания с ограничением на длину очереди

Одноканальная СМО с ограничением на длину очереди. СМО

содержит один обслуживающий канал. На вход поступает простейший поток заявок с интенсивностью X. Если заявка застала обслуживающий канал занятым, то она встает в очередь и ожидает начала обслуживания. Число мест в очереди ограничено и равно т. Если заявка застала обслуживающий канал занятым и в очереди нет свободных мест, то она покидает систему необслу- женной.
2. Что такое переходные вероятности и в чем их отличие от вероятностей состояний

Переходной вероятностью называют условную вероятность того, что из состояния (в котором система оказалась в результате некоторого испытания, безразлично какого номера) в итоге следующего испытания система перейдет в состояние. Таким образом, в обозначении первый индекс указывает номер предшествующего, а второй − номер последующего состояния.

Для неоднородной марковской цепи вектор-строка вероятностей состояний от k-го до (к + 1 )-го шага равна произведению вектор-строки вероятностей состояний от (к - 1)-го до к-го шага на матрицу переходных вероятностей от к-го до (к + 1)-го шага к= 1,2
3. Задача. На АЗС имеется только одна колонка для заправки. Интенсивность потока автомобилей на АЗС к колонке за бензином составляет 30 авто в час. Среднее время заправки равно 5 мин. Проведите анализ работы системы массового обслуживания.



Зав. кафедрой Коккоз М.М._________Разработал Авилова Е.К._________

Утверждено: Протокол № 16А от 28.03.2022г.

Карагандинский технический университет

Экзаменационный билет № 29

Кафедра Информационные технологии и безопасность

Дисциплина «Теория массового обслуживания»

Образовательная программа 6В06301– Системы информационной безопасности
1. Какая Марковская цепь называется непрерывной?

Марковский случайный процесс с дискретными состояниями и непрерывным временем называется непрерывной цепью Маркова при условии, что переход системы из состояния в состояние происходит не в фиксированные, а в случайные моменты времени.

2. Многоканальная система массового обслуживания без ограничений.

В системах массового обслуживания без ограничений теоретически предполагается, что очередь будет расти бесконечно, следовательно, вероятность отказа в обслуживании будет равна нулю.



3. Задача. Среднее число покупателей, поступающих на узел расчета в магазине самообслуживания, 100 человек в час. Кассир может обслуживать 60 человек в час. Определите, какое число кассиров необходимо для того, чтобы вероятность появления очереди не превысила 0,60.

Интенсивность потока обслуживания:



. Интенсивность нагрузки.
ρ = λ*t_обс = 100*1/60 = 1.667

Вероятность, что канал свободен (доля времени простоя каналов).


Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов).
n_з = ρ*p_обс = 1.667*0.375 = 0.625 канала.
Зав. кафедрой Коккоз М.М._________Разработал Авилова Е.К._________

Утверждено: Протокол № 16А от 28.03.2022г.