Практичнеское занятие №1. Вероятность безотказной работы или функция надежности P(t)
 Скачать 68.3 Kb.
|
|
Вероятность безотказной работы или функция надежности P(t) выражает вероятность того, что невосстанавливаемый объект не откажет к моменту времени наработки t. Дополнение вероятности безотказной работы до единицы 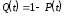  называется вероятностью отказа или функцией ненадежности. Вероятность отказа Q(t) - вероятность того, что случайное время до отказа меньше заданного времени t В результате испытаний можно определить P(t) лишь приближенно, в виде статистической оценки, обозначаемой тильдой, т.е.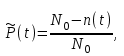 где n(t) – количество объектов, отказавших к моменту времени t, при их исходном количестве N0. Плотность распределения наработки до отказа называют частотой отказов. Экспериментально частота отказов определяется как отношение числа отказавших объектов в единицу времени к первоначальному числу объектов при условии, что все вышедшие из строя объекты не восстанавливаются. Согласно этому определению 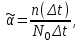 где n(t) – число отказавших объектов в интервале времени от t - t/2 до t + t/2. Средняя наработка 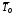до отказа  определяется как математическое ожидание времени до первого отказа. Средняя наработка до отказа является средним показателем и не отражает характер распределения времени до отказа.По статистическим данным об отказах средняя наработка до первого отказа вычисляется по формуле 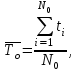 где ti – время безотказной работы i- го объекта. Интенсивность отказов (t) выражает интенсивность процессов возникновения отказов. Статистическая интенсивность отказов определяется отношением числа отказавших объектов в единицу времени к среднему числу объектов, исправно работающих в данный отрезок времени. 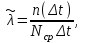 где 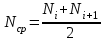 - среднее число исправно работающих объектов в интервале t; Ni – число объектов, исправно работающих в начале интервала t; Ni+1 – число объектов, исправно работающих в конце интервала t.Вероятностная оценка этой характеристики находится из выражения 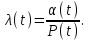 Наиболее распространенной статистической моделью надежности является экспоненциальная модель распределения времени до отказа, по которой вероятность безотказной работы объекта выражается зависимостью 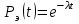 ,где - параметр модели (интенсивность отказов) Пусть отказы элементов есть независимые друг от друга события. Так как система работоспособна, если работоспособны все ее элементы, то согласно теореме об умножении вероятностей вероятность безотказной работы системы Рс (t) равна произведению вероятностей безотказной работы ее элементов: 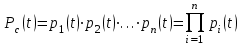 ,где 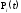 - вероятность безотказной работы i-го элемента.Пусть для элементов справедлив экспоненциальный закон распределения надежности и известны их интенсивности отказов. Тогда и для системы справедлив экспоненциальный закон распределения надежности: 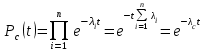 ,где 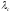 - интенсивность отказов системы.Интенсивность отказов нерезервированной системы равна сумме интенсивностей отказов ее элементов: 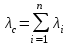 .Если все элементы данного типа равнонадежны, то интенсивность отказов системы будет 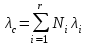 ,где: 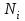 - число элементов i-го типа; r – число типов элементов.Выбор 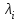 для каждого типа элементов производится по соответствующим таблицам.Среднее время наработки до отказа и частота отказов системы соответственно равны: 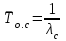 ,  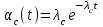.В резервированной системе отказ какого-либо элемента не обязательно приводит к отказу всей системы. Типичным случаем является логически параллельное соединение элементов (рис.2), при котором система отказывает тогда, когда отказывают все ее элементы. Такой тип резервирования называют постоянным или нагруженным (m-1)-кратным резервированием. В этом случае все элементы выполняют одну и ту же функцию, работают одновременно и равнонадежны. По теореме умножения вероятностей имеют место следующие выражения: 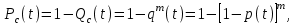 где q(t), p(t) – соответственно вероятности отказа и безотказной работы одного элемента. 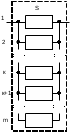 Рис.2. Схема логического соединения элементов резервированной системы Если для элементов справедлив экспоненциальный закон распределения надежности, то 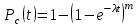 . |