13 Вычисление вероятностей состояния смо
 Скачать 31.65 Kb.
|
|
13) Вычисление вероятностей состояния СМО. Что будет происходить с вероятностями состояний при  ? Будут ли  стремиться к каким-либо пределам? Если эти пределы существуют и не зависят от начального состояния системы, то они называются финальными вероятностями состояний. где  - конечное число состояний системы.Финальные вероятности состояний – это уже не переменные величины (функции времени), а постоянные числа. Очевидно, что:  Финальная вероятность состояния  – это по–существу среднее относительное время пребывания системы в этом состоянии.Например, система S имеет три состояния S1, S2 и S3. Их финальные вероятности равны соответственно 0,2; 0,3 и 0,5. Это значит, что система в предельном стационарном состоянии в среднем 2/10 времени проводит в состоянии S1, 3/10 – в состоянии S2 и 5/10 – в состоянии S3. Вероятности свободного состояния СМО: Многоканальная с отказами P0 =  Или как давал препод:  i=1,R  Многоканальная СМО с ожиданием и ограничением на длину очереди P0 =  Многоканальная СМО с ожиданием P0 =  14) Испытание и исследование свойств имитационной модели После того, как имитационная модель реализована на ЭВМ, необходимо провести испытание, проверку достоверности модели. Это является чрезвычайно важным и ответственным моментом в имитационном моделировании. Проверка, выполненная не тщательно, может привести к неизвестным последствиям. На этапе испытания и исследования разработанной имитационной модели организуется комплексное тестирование модели (testing) -планируемый итеративный процесс, направленный главным образом на поддержку процедур верификации и валидации имитационных моделей и данных.Если в результате проведенных процедур модель окажется недостаточно достоверной, может быть выполнена калибровка имитационной модели (в моделирующий алгоритм встраиваются калибровочные коэффициенты) с целью обеспечения адекватности модели, или в более сложных случаях возможны многочисленные итерации на ранние этапы с целью получения дополнительной информации о моделируемом объекте или доработки имитационной модели. Наличие ошибок во взаимодействии компонент модели возвращает исследователя к этапу создания имитационной модели. Возможно, в ходе формализации исследователь слишком упростил физические явления, исключил из рассмотрения ряд важных сторон функционирования системы, что привело к неадекватности модели объекту. В этом случае исследователь должен вернуться к этапу формализации системы. В тех случаях, когда выбор способа формализации оказался неудачным, исследователю необходимо повторить этап составления концептуальной модели с учетом новой информации и появившегося опыта. Наконец, когда у исследователя оказалось недостаточно информации об объекте, он должен вернуться к этапу составления содержательного описания системы и уточнить его с учетом результатов испытания. 15) Проверка адекватности модели Проверка адекватности модели проводится только в случае ненасыщенного планирования на основе сопоставления дисперсии воспроизводимости среднего значения функции отклика s2(y) и дисперсии адекватности. Оценка дисперсии адекватности при N > m характеризует отклонения между результатами наблюдений и значениями, формируемыми по функции отклика 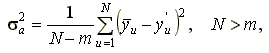 ,где m – количество оцениваемых коэффициентов модели;  – среднее значение результатов наблюдения в u-й точке плана;y'u – значение отклика в этой же точке, предсказанное на модели. Количество степеней свободы дисперсии адекватности ja = N – m. При насыщенном планировании нет степеней свободы и сумма отклонений равна нулю. Проверка адекватности сводится к проверке гипотезы об однородности оценки дисперсии воспроизводимости s2 (y) с количеством степеней свободы j(y) и оценки дисперсии адекватности. Проверка осуществляется по критерию Фишера аналогично рассмотренной выше проверке однородности дисперсий воспроизводимости. Оценки дисперсий в формуле расчета критерия расставляются так, чтобы его величина была больше единицы, критическая область является двусторонней. Если вычисленное значение критерия меньше критического, то нет оснований для сомнений в адекватности модели. Однако положительный исход статистической проверки не гарантирует достоверной адекватности, а тем более истинности модели (хотя и не противоречит такому предположению). Когда гипотеза отклоняется, следует вывод о неадекватности модели, следовательно, она заведомо не является истинной. Дальнейшее применение неадекватной модели обычно нецелесообразно, и надо принять меры по ее совершенствованию. Причиной неадекватности могут являться: ошибки в организации и проведении опытов, например неконтролируемое изменение неучтенных в модели факторов; погрешности в задании исходных данных и в измерении результатов; большой размах варьирования факторов и другие причины. Иначе говоря, анализ причин неадекватности требует серьезного изучения сущности исследуемого процесса и методов его исследования. 20) Основные типы и цели вычислительного эксперимента в имитационном моделировании Целями вычислительного эксперимента могут быть: - оценка выходных переменных функционирования сложной системы при заданных параметрах системы; - выбор на множестве альтернатив; - получение знаний о влиянии управляемых параметров на результаты эксперимента; - определение тех значений входных параметров и переменных, при которых достигается оптимальный выход (отклик). Наиболее широко на практике распространены следующие типы вычислительных экспериментов, представленные в таблице 7.2.: Таблица 7.2 Основные типы направленных вычислительных экспериментов
1 тип: Оценка и сравнение средних и дисперсий различных альтернатив. 2 тип: Анализ чувствительности (параметрический анализ) системы к изменению параметров. Основным содержанием такого эксперимента является определение влияния управляемых параметров, переменных (факторов) на результаты экспериментов (отклик). В эксперименте 2 типа ставится математическая задача интерполяции и осуществляется построение интерполяционных формул. Например, модель F на рис.7.1.1. может быть аппроксимирована полиномиальной функцией, например некоторой линейной регрессионной моделью. В задачах интерполяции необходимо найти функцию F. 3 тип: Решается задача оптимизации: поиск оптимальных значений на некотором множестве возможных значений переменных. В задачах оптимизации необходимо найти экстремум функции F. 4 тип: Вариантный синтез, это более сложный класс вычислительных экспериментов, как правило, связанный с многокритериальной оптимизацией, реализацией итерационных имитационно-оптимизационных процедур [13], выбором и принятием решения в широком смысле слова. Рассмотрение этих методов в этой лекции мы не будем проводить. Рассмотрим основные математические модели и методы, применяемые в первых трех типах вычислительных экспериментов и общие схемы по их организации и проведению. Эксперименты первого типа довольно просты и обычно являются так называемыми однофакторными экспериментами, подробнее рассматриваются в разделе 7.4. Основные вопросы, встающие перед экспериментатором при их проведении, — это вопросы о размере выборки, начальных условиях, наличие или отсутствии автокорреляции и другие задачи тактического планирования машинного эксперимента, которые рассматриваются подробнее в соответствующем разделе учебника. Основные математические методы, применяемые и рекомендуемые в этом эксперименте: статистические методы оценивания путем использования таких величин, как среднее значение, стандартное отклонение, коэффициент корреляции др.; процедуры проверки гипотез с использованием стандартной тестовой статистики (t, F, 2 и др.), однофакторный дисперсионный анализ; при сравнении и выборе альтернатив Клейнен [20] рекомендует статистические процедуры ранжирования (веса) и отбора: методы множественного ранжирования и методы множественного сравнения; в более сложных случаях могут быть полезны различные эвристические приемы. Эксперименты второго типа предполагают обычно широкое использование методов планирования эксперимента, которые мы подробно будем изучать в следующем разделе учебника. Основными методами истолкования результатов этих экспериментов являются дисперсионный и регрессионный анализы. Для исследования динамических рядов (в моделях системной динамики) рекомендуется спектральный анализ. В терминах теории планирования экспериментов вход модели называется фактором, конкретные значения фактора -уровнями, выход модели -откликом. План эксперимента определяет комбинацию уровней и для каждой комбинации задает число повторных прогонов модели. Выбирают и осуществляют план, далее, используя данные эксперимента, определяют параметры регрессионной модели. Общая схема исследования здесь следующая: Выбор ограниченного числа прогонов вариантов системы решается с помощью статистических методов планирования экспериментов. Используют полные и дробные факторные планы; В ходе обработки результатов эксперимента получают параметры регрессионной модели; Исследователь выполняет анализ модели (регрессионной зависимости). 3 тип вычислительного эксперимента, ориентированный на решение задачи оптимизации (определяются такие значения управляемых параметров и переменных, которые максимизируют или минимизируют заданную целевую функцию), предполагает использование последовательных или поисковых методы построения экспериментов. Полезно применение методологии анализа поверхности отклика, рассматриваемой в последующих разделах этой лекции, комбинирующей эти методы планирования и итерационные имитационно-оптимизационные вычислительные процедуры. Принципы оптимизации здесь те же, что и для аналитических моделей, однако выход имитационной модели содержит случайную составляющую, поэтому необходимо в вероятностной форме задавать ограничения на отклики и осуществлять статистическую интерпретацию значений целевой функции. |