|
Тема 0. Погрешности
№
вопроса
|
Вопросы
|
Варианты ответов
|
1
|
один их подходов к упрощению математической модели состоит в
|
Выявлению факторов, влияние которых пренебрежимо мало в данных условиях
Сведении к минимуму средней погрешности исходных данных
Сведении к минимуму дисперсии ошибок округления
Увеличении скорости сходимости итерационного процесса
|
2
|
цель прямой задачи математического моделирования состоит в том, чтобы
|
При известных входных переменных объекта рассчитать выходные переменные без учета параметров
При известных входных и расчетных выходных переменных объекта рассчитать параметры модели
Определить вид и структуру математической модели
При известных параметрах и входных переменных объекта рассчитать выходные переменные
|
3
|
модели динамических систем часто реализуются в виде
|
системы линейных уравнений высокого порядка
задачи Коши для системы обыкновенных дифференциальных уравнений
переопределенных систем линейных уравнений
интегральных уравнений Фредгольма
|
4
|
К наиболее распространенным признакам, по которым классифицируются модели являются
|
цель исследования
область знаний
фактор времени
все вышеперечисленное
|
5
|
К устранимым погрешностям относят
|
Погрешность метода, погрешность вычислений
|
6
|
Как называется погрешность численного метода, обусловленная неточным заданием входных данных?
|
Погрешность входных данных
|
7
|
Как вычислить абсолютную погрешность
|
Абсолютной погрешностью называется модуль разности точного и приближенного значений величины
Абсолютной погрешностью называется разность точного и приближенного значений величины
Абсолютную погрешность получают как модуль разности точного и приближенного значений величины, деленный на точное значение
Абсолютную погрешность получают как модуль разности точного и приближенного значений величины, деленный на приближенное значение
|
8.
|
Относительная погрешность вычислений это:
|
1. Результат деления двух значений вычисления.
2. Отношение двух приближенных значений вычисляемой величины.
3. Отношение абсолютной погрешности вычислений к истинному значению.
4. Точность вычисления.
|
9.
|
Абсолютная погрешность вычислений это:
|
1. Точность вычисления.
2. Разность между значением величины и ее приближением.
3. Абсолютная величина разности между значением вычисляемой величины и ее приближенным значением.
4. Отклонение приближенного значения величины от ее истинного значения.
|
10.
|
При уточнении корня уравнения на заданном отрезке по методу Ньютона получены значения корня на трех итерациях 4,601; 4,405; 4,407. Определите погрешность вычисления:
|
1. 0,002.
2. 0,1
3. 0,012.
4. 0,01.
|
11.
|
При уточнении корня уравнения на заданном отрезке по методу Ньютона получены значения корня на трех итерациях 5,031; 4,306; 4,303. Определите погрешность вычисления:
|
1. 0,003.
2. 0,1
3. 0,06.
4. 0,004.
|
Тема 1. Вычисление определенных интегралов
№
вопроса
|
Вопросы
|
Варианты ответов
|
1
|
Составная формула парабол для приближенного вычисления определенного интеграла 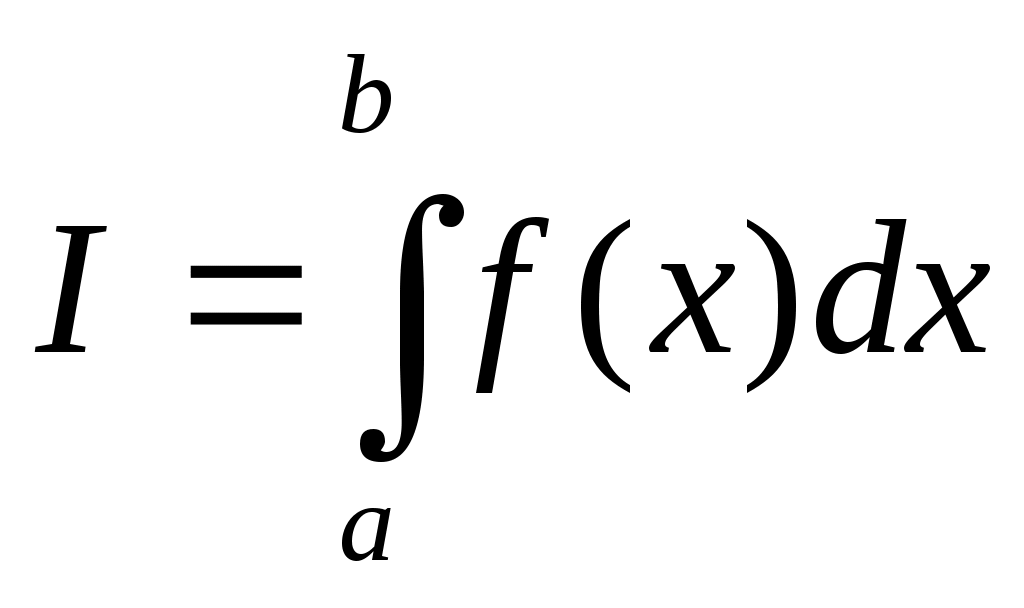 имеет вид … имеет вид …
|
1. 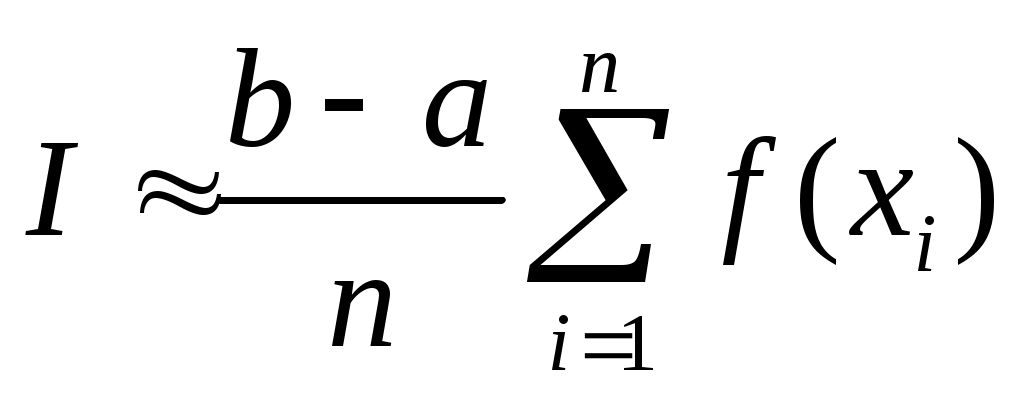
2. 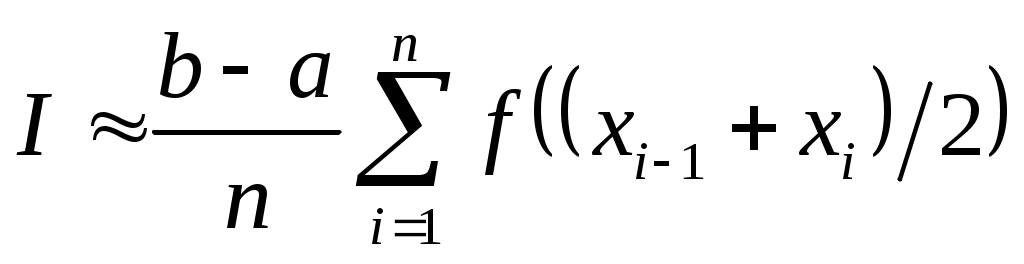
3. 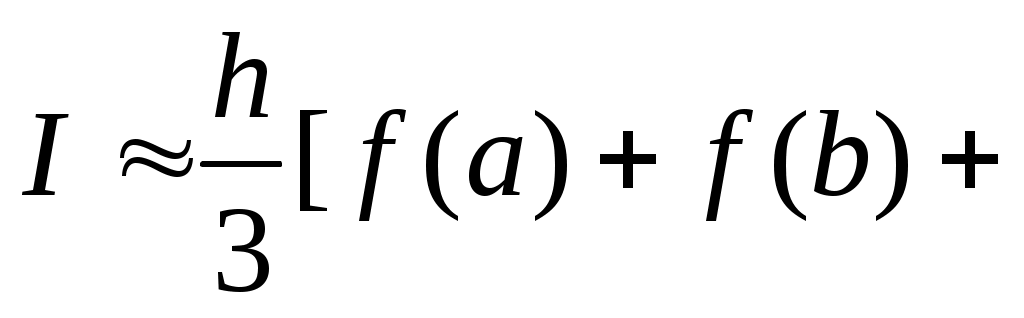
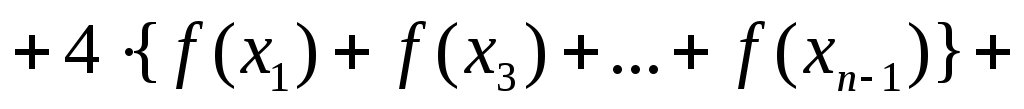
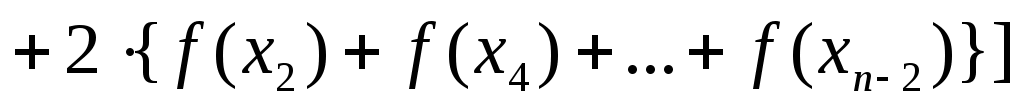
4. 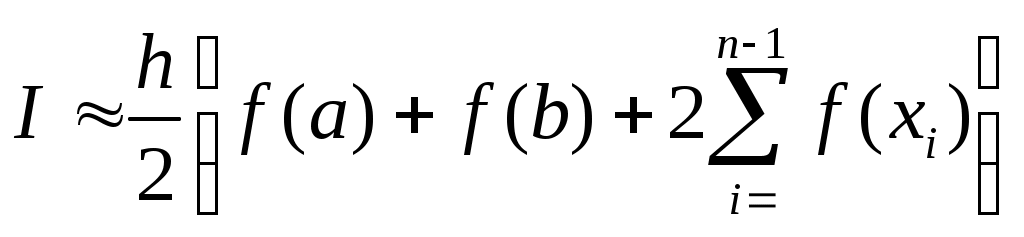
|
2
|
При приближенном вычислении интеграла методом средних прямоугольников на каждом частичном промежутке [xi ; xi+1] график подынтегральной функции заменяется …
|
1. отрезком прямой, проходящей через точку (xi+1/2; yi+1/2) параллельно оси абсцисс.
2.отрезком прямой, проходящей через точку (xi; yi) параллельно оси абсцисс.
3. отрезком прямой, проходящей через точки (xi; yi) и (xi+1; yi+1).
4. частью параболы, проходящей через точки (xi; yi), (xi+1; yi+1) и (xi+2; yi+2).
|
3.
|
Оценка погрешности составной формулы левых прямоугольников равна ...
|
1. 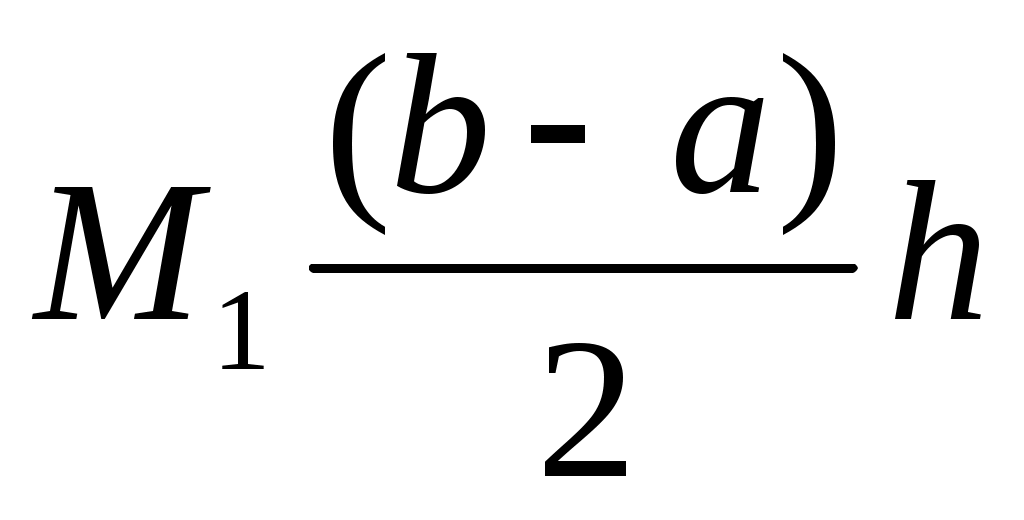
2. 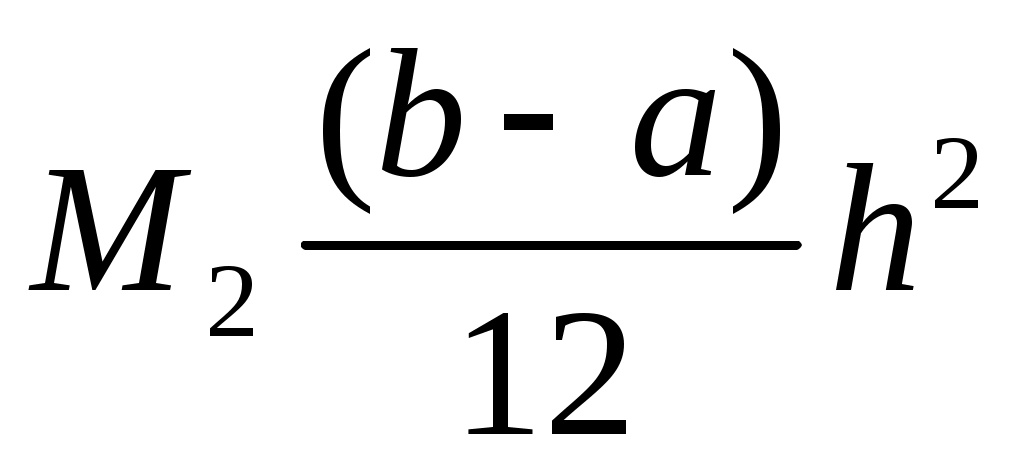
3. 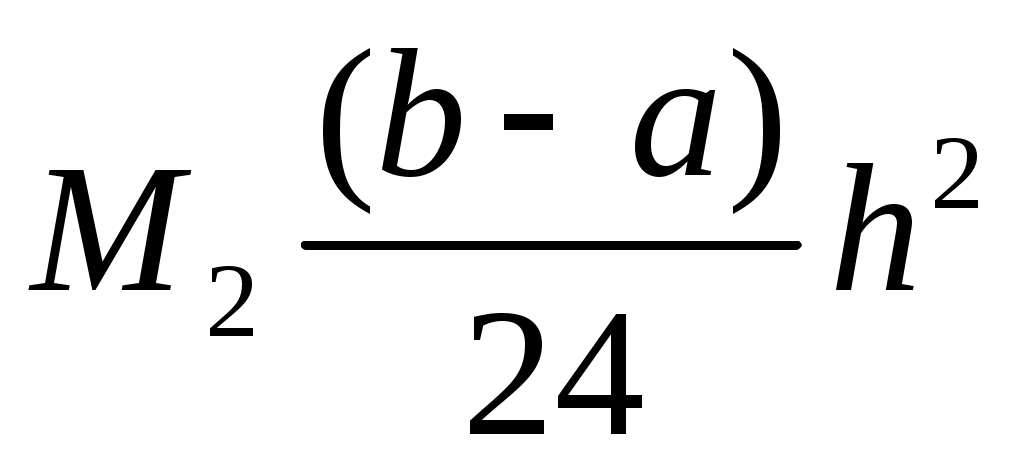
4. 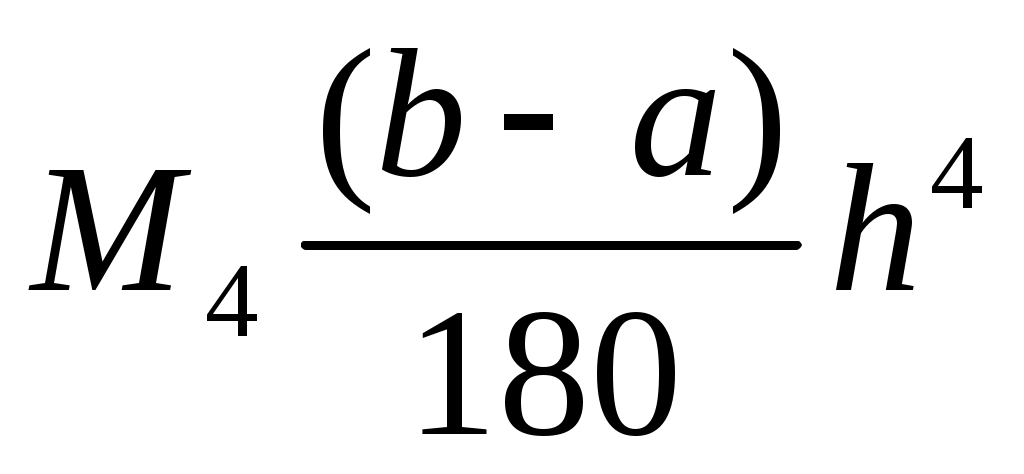
|
|
Оценка погрешности составной формулы левых прямоугольников равна ...
|
1. 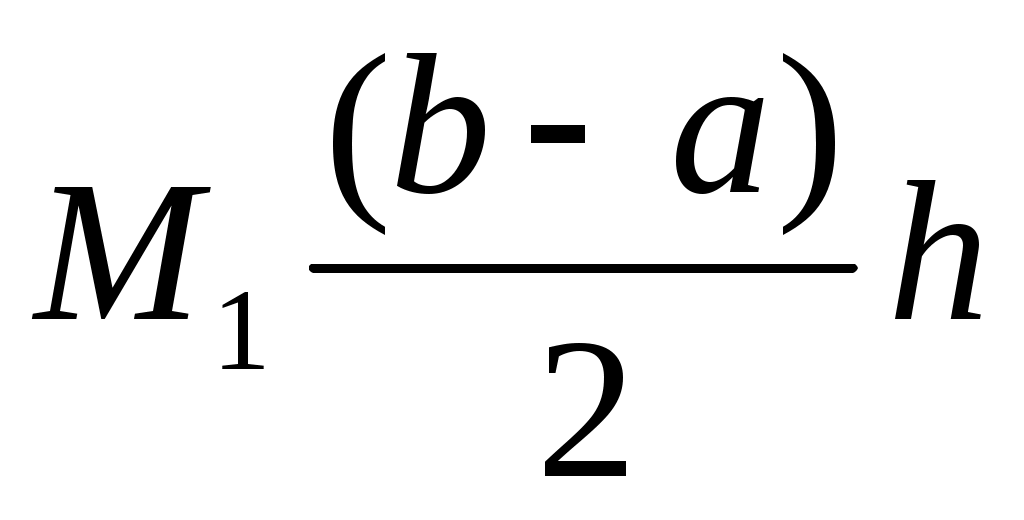
2. 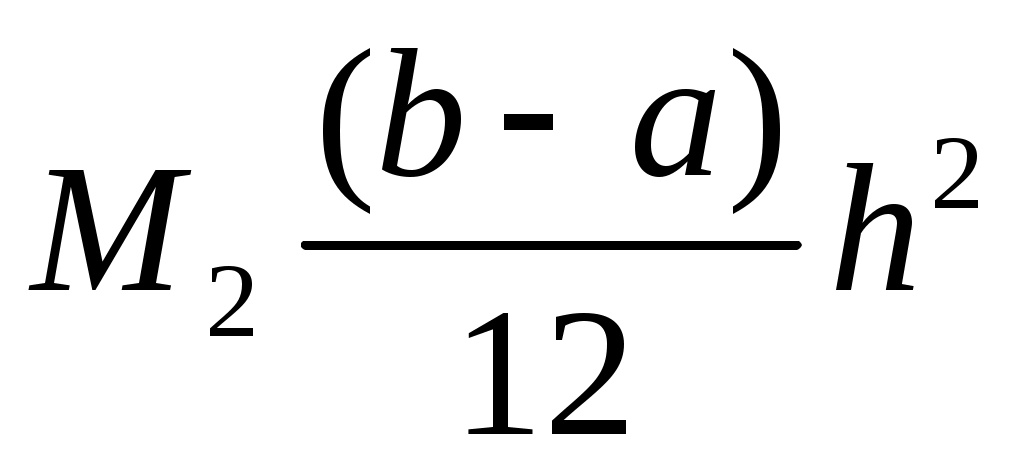
3. 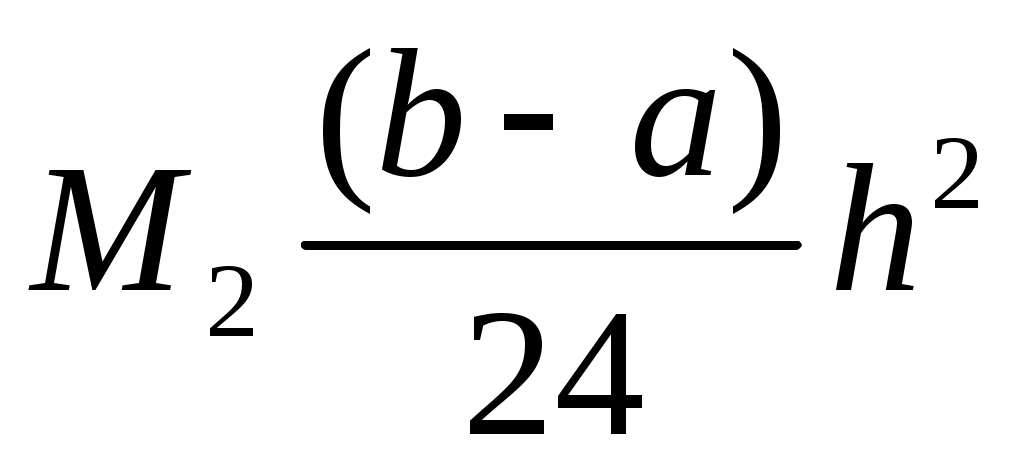
4. 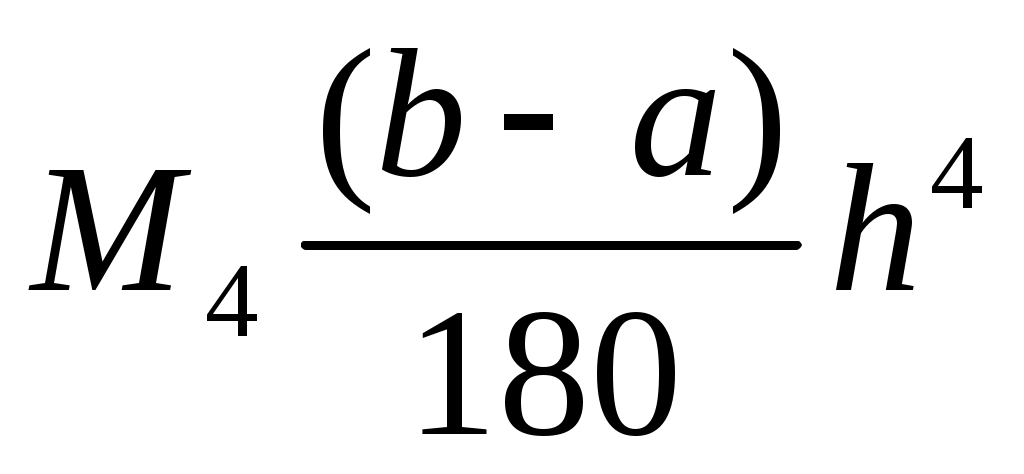
|
4
|
какой алгоритм применяется системой Mathcad для численного интегрирования?
|
Алгоритм Ротберга
Метода Симпсона
Метод Монте-Карло
Вычисление с использованием первообразной
|
5
|
Формулы приближенного вычисления определенного интеграла основываются на
|
Определении определенного интеграла
Геометрическом свойстве определенного интеграла
Арифметическом свойстве определенного интеграла
Формуле Ньютона-Лейбница
|
6
|
При оценке точности вычисления определенного интеграла 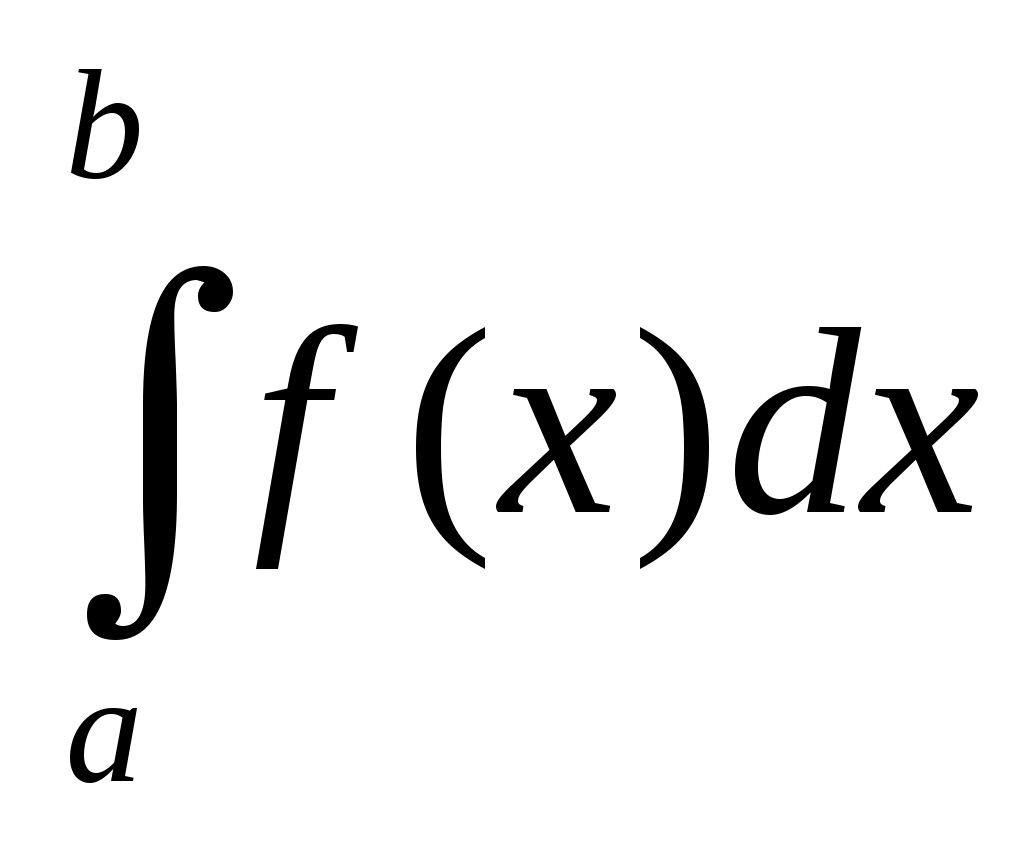 по формуле трапеций используется значение по формуле трапеций используется значение
|
Первой прозводной f(x)
Второй производной f(x)
Третьей производной f(x)
Четвертой производной f(x)
|
7
|
При оценке точности вычисления определенного интеграла 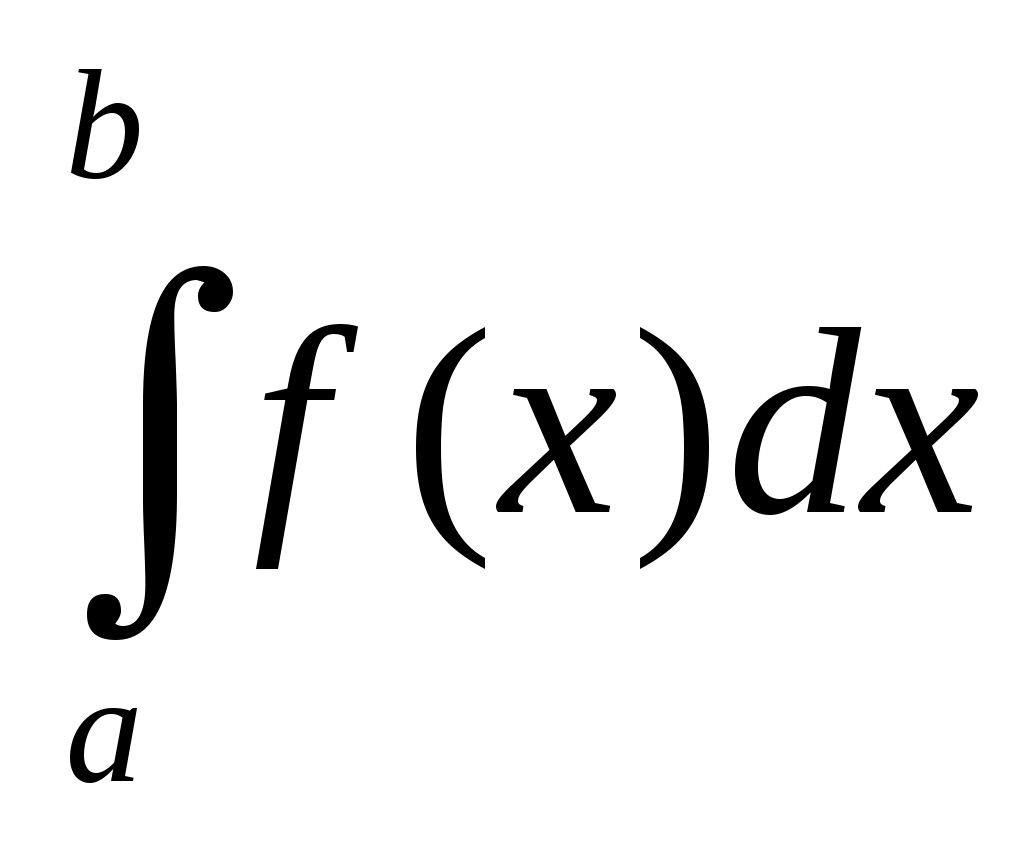 по формуле Симпсона используется значение по формуле Симпсона используется значение
|
Первой прозводной f(x)
Второй производной f(x)
Третьей производной f(x)
Четвертой производной f(x)
|
Тема 2. Интерполяция и аппроксимация
№
вопроса
|
Вопросы
|
Варианты ответов
|
1.
|
Интерполяционный многочлен Лагранжа построенный по точкам (x1, y1)=(2, 3), (x2, y2)=(4, 4)
|
1. 2(x-2) - (3/2)(x-4)
2. 2(x-2) - 4(x-4)
3. 2(x-2) + (3/2) (x-4)
4. 3(x-2) - 4(x-4)
5. 3(x-2) + 4(x-4).
|
2.
|
Интерполяционный многочлен Лагранжа построенный по точкам (x1, y1)=(2, 3), (x2, y2)=(4, 2), (x3, y3)=(5, 6)
|
1. 0,5(x-4)(x-5)-(x-2)(x-5)+2(x-2)(x-4)
2. 3(x-4)(x-5)+2(x-2)(x-5)+6(x-2)(x-4)
3. 3(x-4)(x-5)-2(x-2)(x-5)+6(x-2)(x-4)
4. (x-4)(x-5)-(x-2)(x-5)+(x-2)(x-4)
|
3
|
в чем состоит задача интерполяции функции
|
В построении линии, отражающей тенденцию изменения данных
В вычислении интеграла от функции
В построении линии, проходящей точно через заданные точки
В вычислении частных производных функции
|
4
|
функции системы Mathcad cspline, pspline, lspline предназначены
|
Для линейной интерполяции данных
Вычисления вектора вторых производных перед спланинтерполяцией
Для вычисления коэффициентов интерполяционного полинома Лагранжа
Нет таких функций
|
5
|
в чем состоит задача аппроксимации функции
|
В построении линии, отражающей тенденцию изменения данных
В вычислении значения функции
В вычислении значения функции, заданной таблично, в точке с помощью функции максимально близко проходящей около точек таблицы
В вычислении значения функции, заданной таблично, в точке с помощью функции проходящей через точки таблицы
|
6
|
основная идея метода наименьших квадратов состоит в том, чтобы
|
по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция проходила через узловые точки
по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция не проходила через узловые точки
по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция могла как проходить через узловые точки, так и не проходить
по данным эксперимента построить приближенную функцию таким образом, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальной
по данным эксперимента построить приближенную функцию таким образом, чтобы сумма отклонений построенной функции от экспериментальной в узловых точках была минимальной
|
Тема 3. Вычисление приближенных значений корней нелинейных уравнений
№
вопроса
|
Вопросы
|
Варианты ответов
|
1
|
решение нелинейного уравнения f(x)=0 начинается с
|
определения знака производной f’(x)
проверки условия сходимости итерационного процесса на отрезке
определение начальных условий для начала итерационного процесса
|
2.
|
Действительный корень уравнения 5x4 - 6 = 0 принадлежит интервалу …
|
1. [1; 1,5].
2. [-1; 0].
3. [0; 1].
4. [2; 3].
|
3.
|
Действительный корень уравнения 3x4 - 8 = 0 принадлежит интервалу …
|
1. [0,5; 1].
2. [-1; 0].
3. [0; 1].
4. [1; 1,5].
|
4.
|
Действительный корень уравнения x3 + 2x2 + 3x - 10= 0 принадлежит интервалу …
|
1. [0,5; 1].
2. [-1; 0].
3. [0; 0,5].
4. [1; 1,5].
|
5.
|
Уравнение 3x4+4x3-x-20=0 может иметь . . . действительных корней.
|
1. четыре или два.
2. ровно два.
3. четыре или два, или ни одного
4. ни одного.
|
6.
|
В уравнении 2x5+4x3-x-10=0 комплексных корней может быть …
|
1. от нуля до пяти.
2. ни одного.
3. только два.
4. четыре или два, или ни одного
|
7.
|
Действительный корень уравнения 4x3 + 3x - 5 = 0 принадлежит интервалу …
|
1. [0,5; 1].
2. [-1; 0].
3. [0; 0,5].
4. [2; 3].
|
8.
|
Корень уравнения x2 - 12=0 отделен на интервале [ 3; 4]. Результат уточнения корня методом
Ньютона (касательных) на первой итерации (x0=4), вычисленный с точностью до одного знака после запятой, равен …
|
1. 2,5.
2. 3,5.
3. 2,9.
4. 3,4.
|
9
.
|
Корень уравнения x3- 15=0 отделен на интервале [ 2; 3]. Результат уточнения корня методом
Ньютона (касательных) на первой итерации (x0=3),
вычисленный с точностью до двух знаков после запятой, равен …
|
1. 2,27.
2. 2,28.
3. 2,29.
4. 2,56.
|
10.
|
Уравнение 5x4+3x3-x-18=0 может иметь . . . действительных корней.
|
1. четыре или два.
2. четыре или два или ни одного.
3. ровно четыре.
4. ровно два.
|
11.
|
В уравнении 5x5+8x3-x-12=0 комплексных корней может быть …
|
1. четыре или два, или ни одного.
2. ни одного.
3. только два.
4. только четыре.
|
12.
|
Корень уравнения x2 - 7 = 0 отделен на отрезке [0; 8]. Три итерации метода половинного деления, используемого при уточнении корня, требуют последовательного выбора промежутков … , на которых остается истинное значение корня.
|
1. на отрезке [0; 8] нет корней
2. [4; 8], [4; 6], [5; 6].
3. [0; 4], [2; 4], [2; 3].
4. [4; 8], [6; 8], [6; 7].
|
13
|
Приближенное значение корня нелинейного уравнения можно вычислить по формуле
|
Трапеции
Эйлера
Ньютона
Гаусса
|
14
|
Надстройка табличного процессора Microsoft Excel «Подбор параметра» предназначена для вычисления
|
Корня нелинейного уравнения
Решения СЛАУ
Решения системы нелинейных уравнений
Приближенного значения интеграла
|
15
|
Надстройка Microsoft Excel «подбор параметра» позволяет вычислить
|
Приближенное значение интеграла
Приближенное значение корня нелинейного уравнения
Приближенное решение системы линейных алгебраических уравнений
Приближенное решение системы нелинейных уравнений
|
16
|
Корень уравнения x2 - 15 = 0 отделен на отрезке [0; 8]. Три итерации метода половинного деления, используемого при уточнении корня, требуют последовательного выбора промежутков … , на которых остается истинное значение корня.
|
1. на отрезке [0; 8] нет корней
2. [0; 4], [2; 4], [2; 3].
3. [0; 4], [2;4] [3; 4].
4. [4; 8], [6; 8], [6; 7].
|
17
|
Для получения приближенного значения корня нелинейного уравнения нельзя использовать метод
|
Деления отрезка пополам
Метод итерации
Формулу Эйлера
Формулу Ньютона
|
18
|
Условием сходимости метода итерации при вычислении приближенного значения корня нелинейного уравнения f(x,y)=0 является условие
|
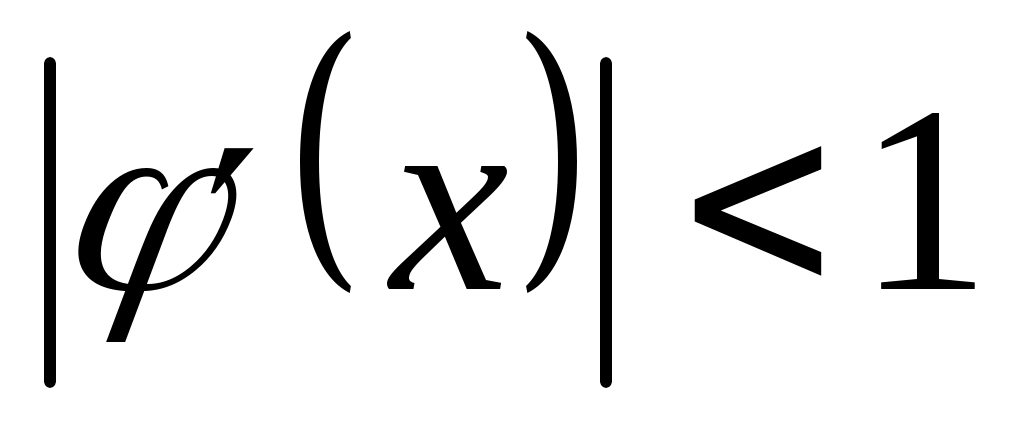
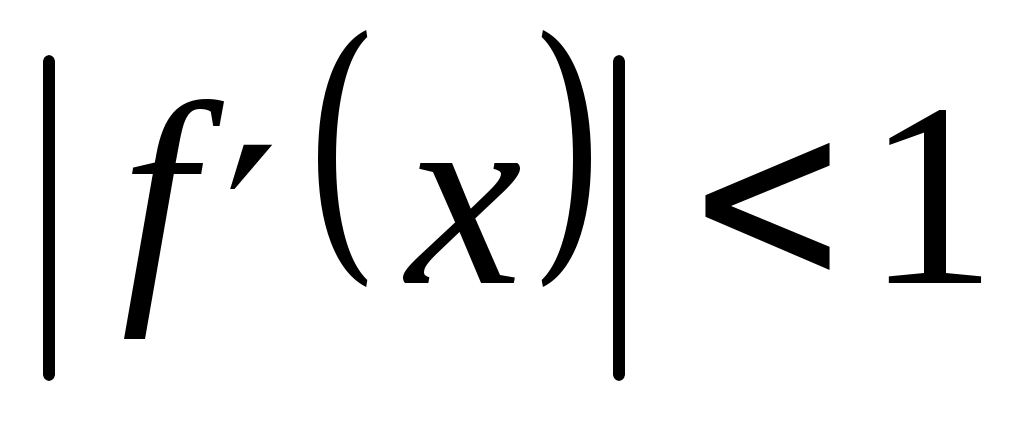
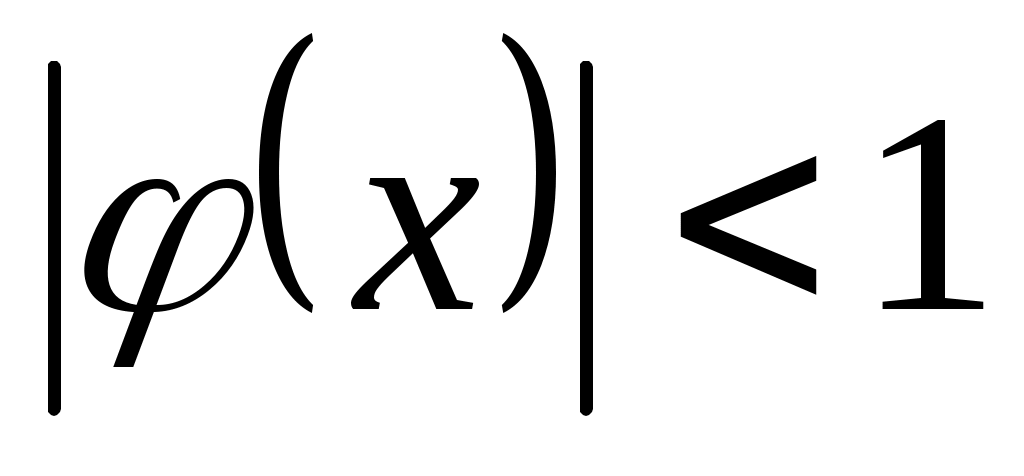
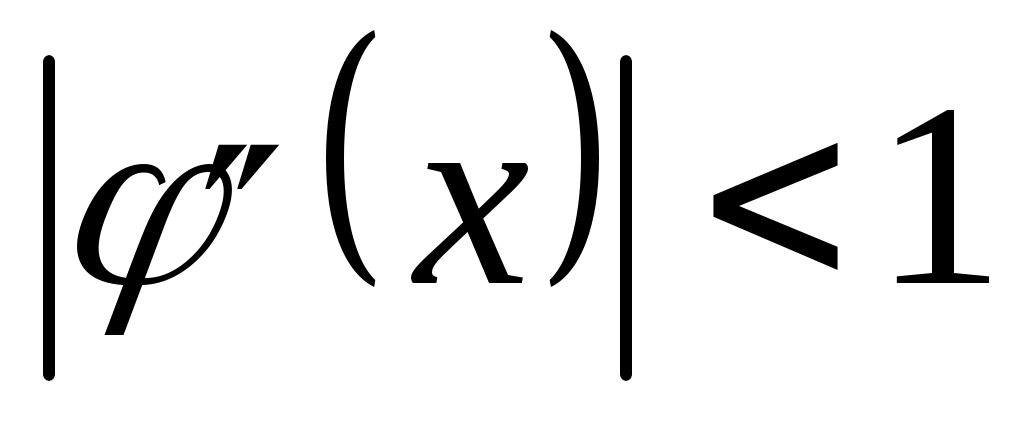
|
19
|
Формула Ньютона для вычисления приближенного значения корня нелинейного уравнения основывается на определении
|
Определенного интеграла
Производной
Геометрическом свойстве определенного интеграла
|
20
|
условием окончания итерационного процесса по методу итерации для решения нелинейного уравнения f(x)=0 является условие
|
Модуль разности приближений меньше точности
Значение модуля функции при xn+1< точности
Одновременное выполнение условий а) б)
Значение функции при xn+1< точности
|
21
|
чему равно значение х2, вычисленное по итерационной формуле 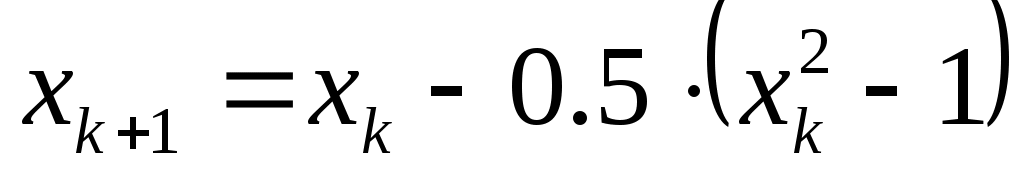 при х0=0 при х0=0
|
0.5
0.875
0.4
0.9
|
Тема 4. Решение СЛАУ
№
вопроса
|
Вопросы
|
Варианты ответов
|
1
|
Для решения систем линейных уравнений применяют итерационные методы ...
|
1. Гаусса.
2. Простых итераций.
3. Зейделя.
4. Верно 2 и 3.
|
2
|
Система линейных уравнений Ax=b с квадратной матрицей A имеет единственное решение, если ее определитель ...
|
1. detA=1
2. detA <0
3. detA≠0
4. detA >0
|
3
|
итерационный численный метод состоит
|
в определении по некоторому математически обоснованному правилу последовательных приближений к решению
в определении точного решения на основе математически строго обоснованных выкладок
в определении точного решения на основе эмпирических соображений
в определении погрешности вычислительного метода
|
4
|
какой метод решения системы линейных уравнений реализует функция lsolve
|
метод квадратных корней
метод простой итерации
метод Гаусса
LU-разложения в произведение треугольных матриц
|
5
|
какой метод решения системы линейных уравнений в блоке given реализует функция find
|
метод квадратных корней
метод простой итерации
метод Гаусса
LU-разложения в произведение треугольных матриц
|
6
|
Метод прогонки позволяет найти решение
|
Системы линейных алгебраических уравнений любого вида
Системы нелинейных уравнений второго порядка
Системы линейных алгебраических уравнений с матрицей коэффициентов трехдиагонального вида
Системы обыкновенных дифференциальных уравнений 1 порядка
|
7
|
Не является точным методом решения СЛАУ
|
Метод Гаусса
Метод прогонки
Метод Зейделя
Метод Крамера
|
8
|
Условием сходимости метода итерации при вычислении приближенного решения системы линейных алгебраических уравнений 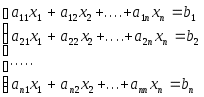
является условие
|
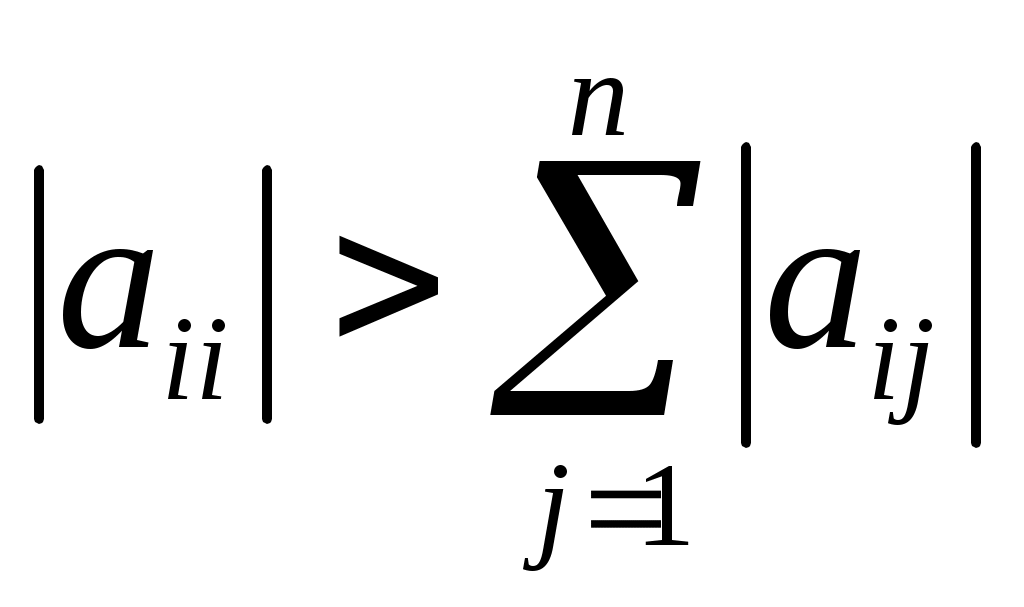 верно верно
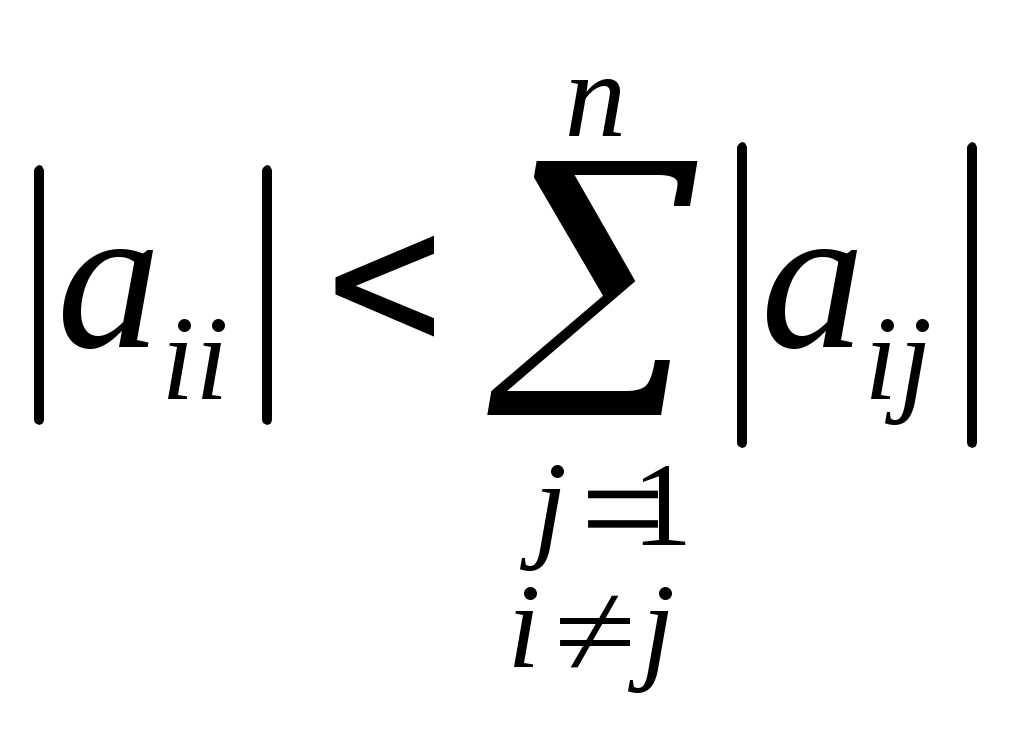
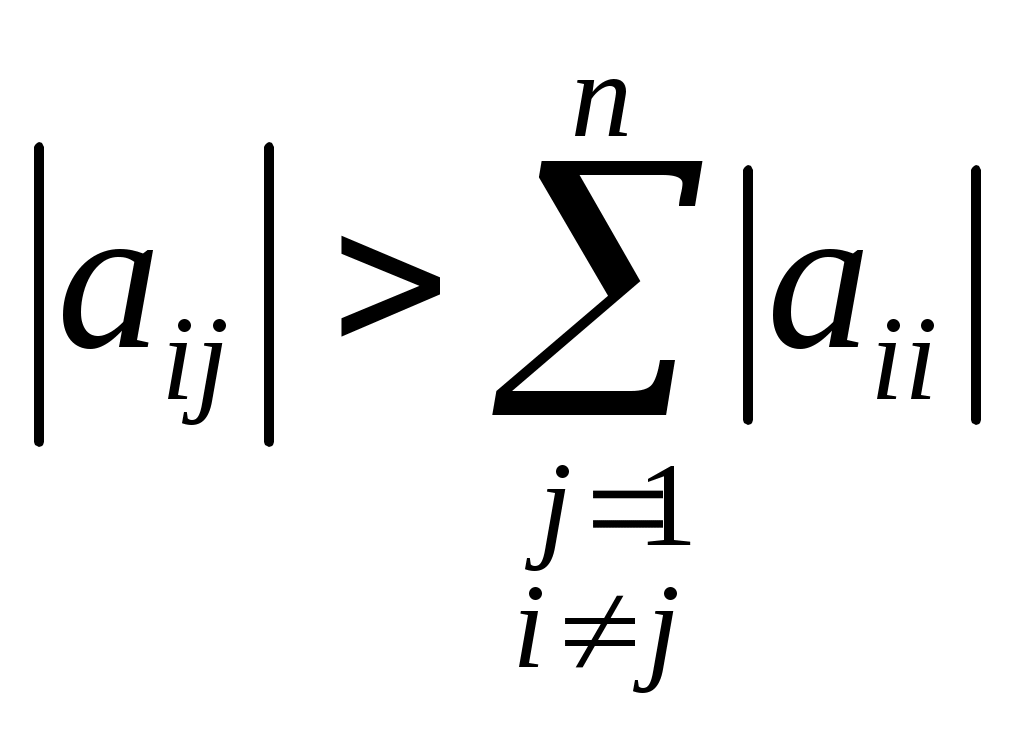
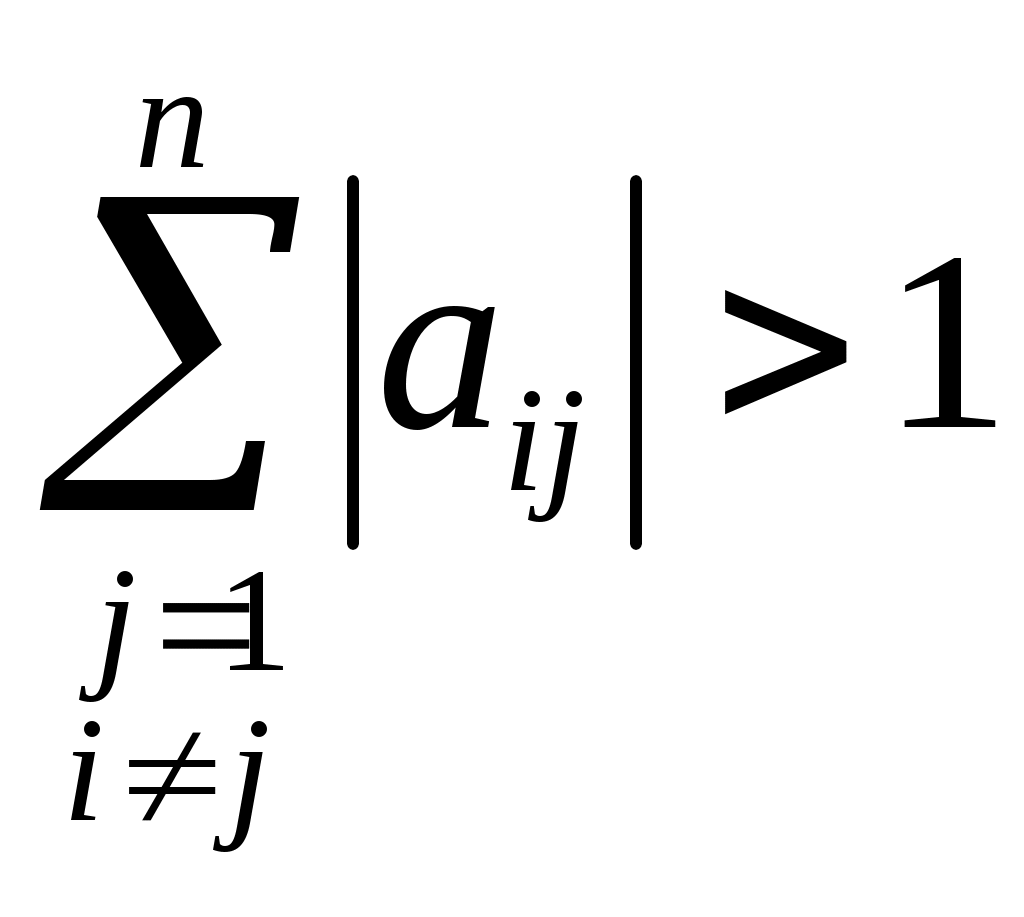
|
9
|
Метод прогонки применяется для решения
|
системы линейных алгебраических уравнений общего вида
системы линейных алгебраических уравнений с матрицей коэффициентов трехдиагонального вида
системы линейных алгебраических уравнений с матрицей коэффициентов пятидиагонального вида
системы нелинейных уравнений
|
10
|
Метод прогонки решения системы линейных алгебраических уравнений похож на метод
|
Гаусса
Крамера
Итерации
Обратной матрицы
|
11
|
Функцию пакета математических расчетов MathCAD find не используют для нахождения
|
Приближенного значения интеграла
Приближенного значения корня нелинейного уравнения
Приближенного решения системы линейных алгебраических уравнений
Приближенного решения системы нелинейных уравнений
|
12
|
Близкими (похожими) являются методы
|
простой итерации и прогонки
простой итерации и итерации Зейделя
прогонки и Гаусса
Эйлера и Рунге-Кутта
Итерации и интерполяции
Интерполяции и аппроксимации
Итерации и Ньютона
|
13
|
в чем суть итерационного метода решения СЛАУ
|
Позволяет найти приближенное решение путем построения последовательности приближений, начиная с некоторого начального приближения
|
14
|
какой метод не относится к прямым методам решения слау
|
Метод Зейделя
|
15
|
чему равняется первое приближение, вычисленное по итерационной формуле по методу Зейделя для решения слау 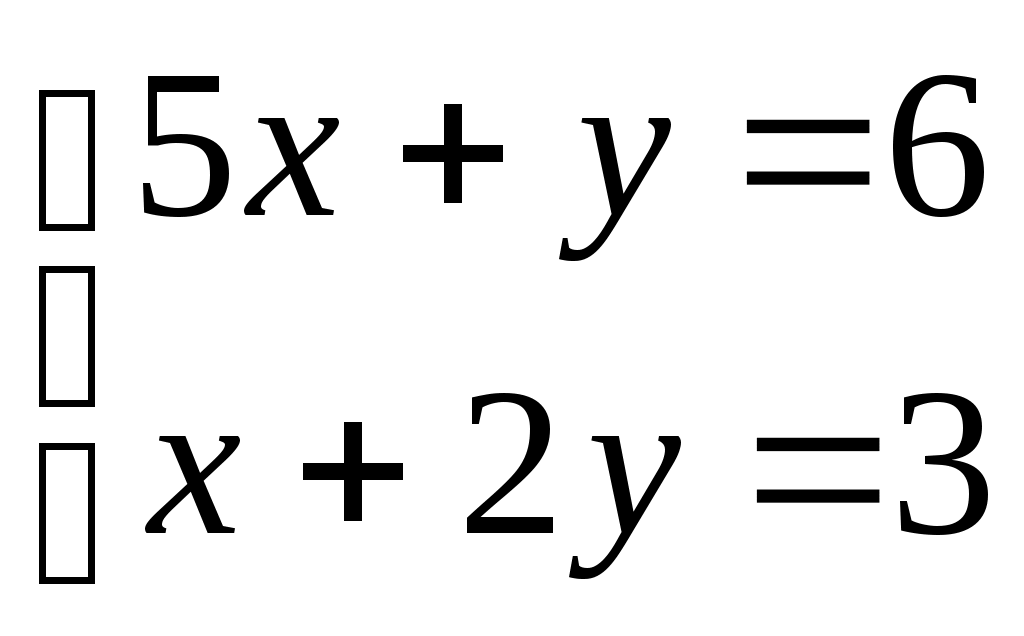 при x0=2 y0=1 при x0=2 y0=1
|
X1=1; y1=0.5
X1=1; y1=1
X1=04 y1=0
X1=0.54 y1=1
|
Тема 5. Вычисление систем нелинейных уравнений
17
|
Надстройка табличного процессора Microsoft Excel «Поиск решения» предназначена для вычисления
|
Корня нелинейного уравнения
Решения СЛАУ
Решения системы нелинейных уравнений
Приближенного значения интеграла
|
18
|
Надстройка Microsoft Excel «поиск решения» позволяет вычислить
|
Приближенное значение интеграла
Приближенное значение корня нелинейного уравнения
Приближенное решение системы линейных алгебраических уравнений
Приближенное решение системы нелинейных уравнений
|
19
|
Условием сходимости метода итерации при вычислении приближенного решения системы нелинейных уравнений 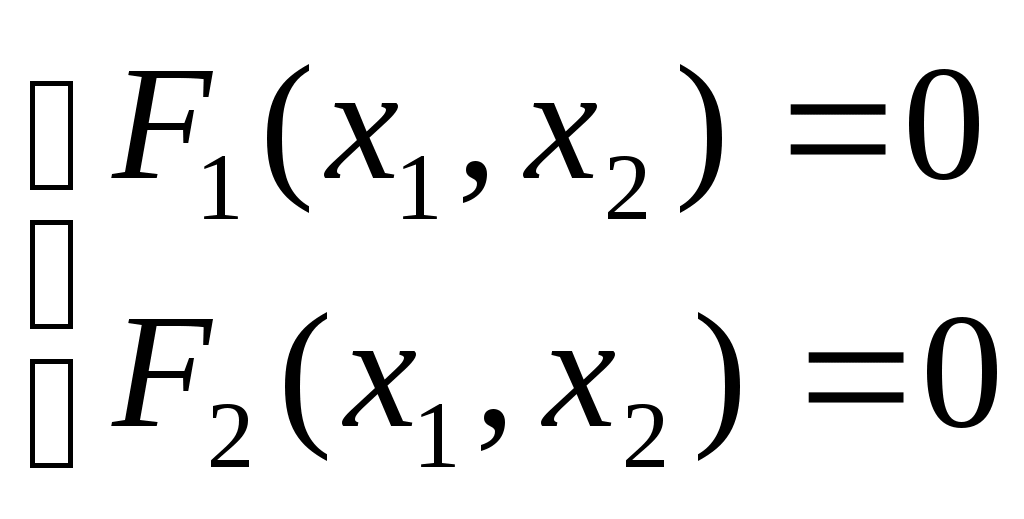 является условие является условие
|
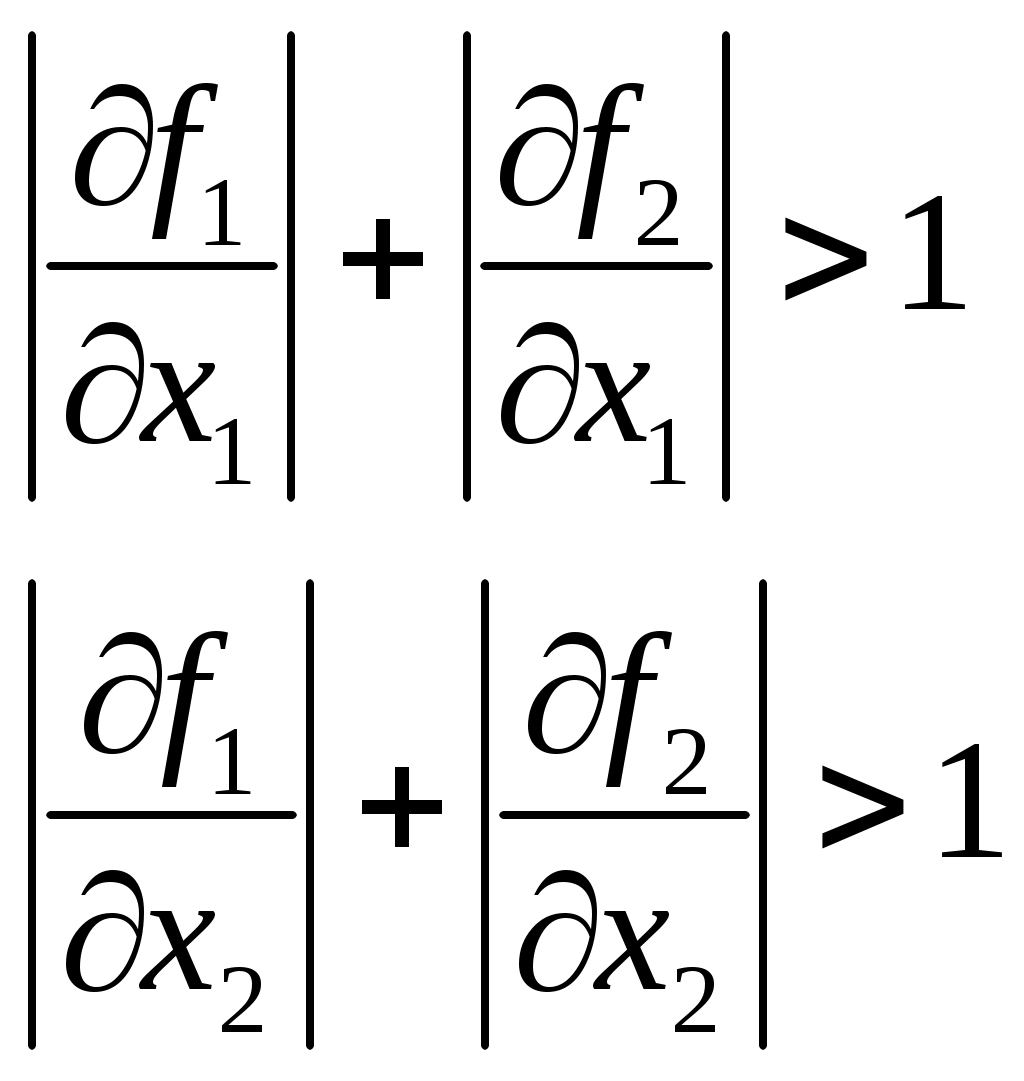
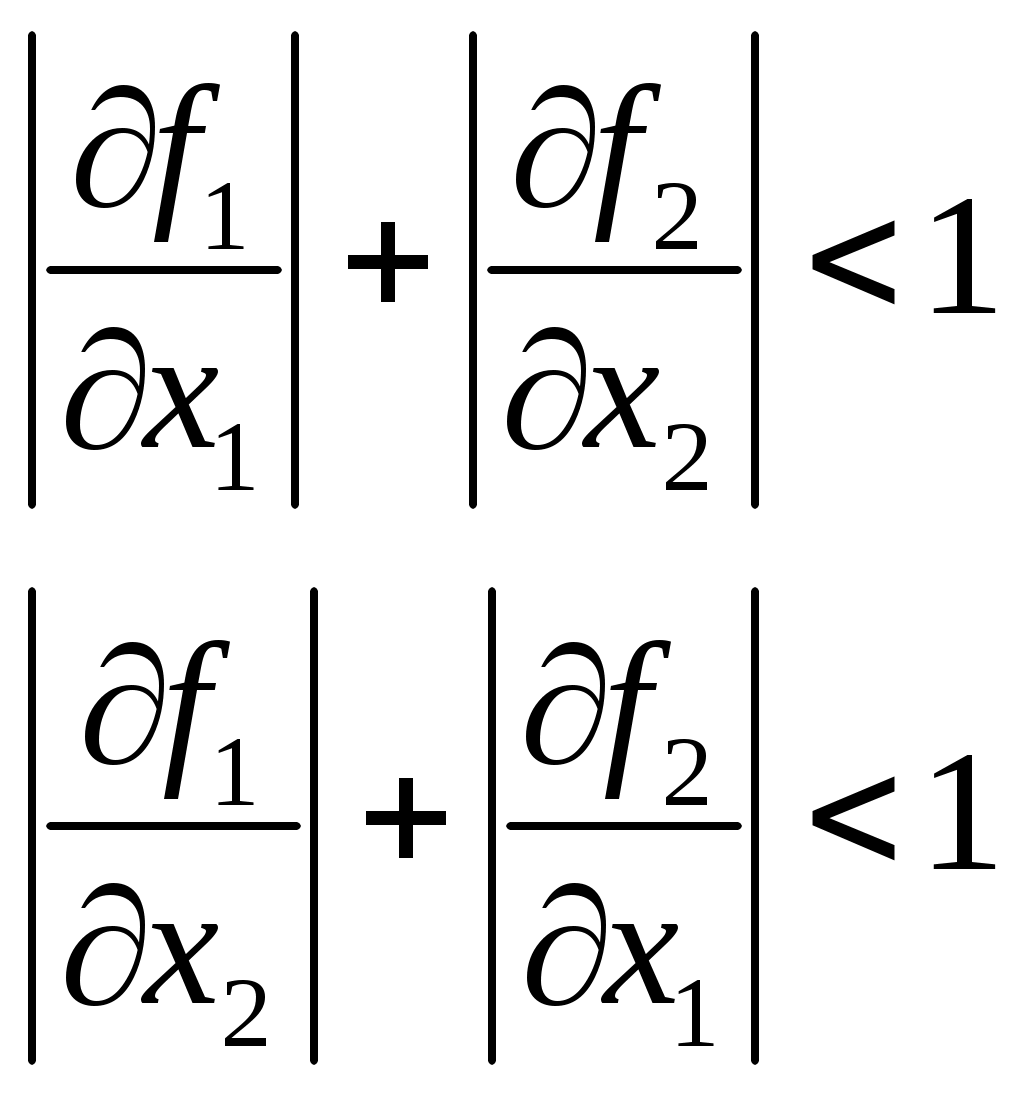
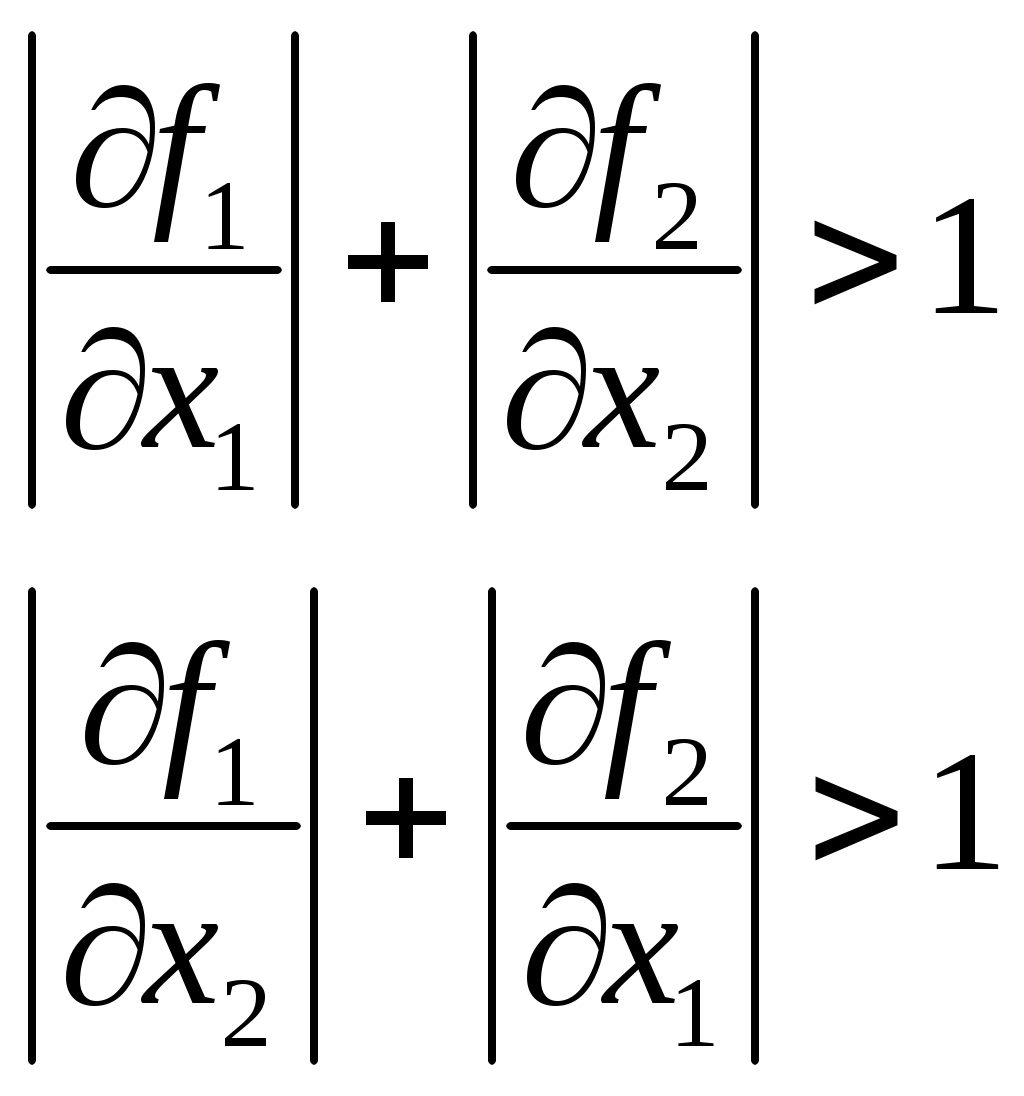
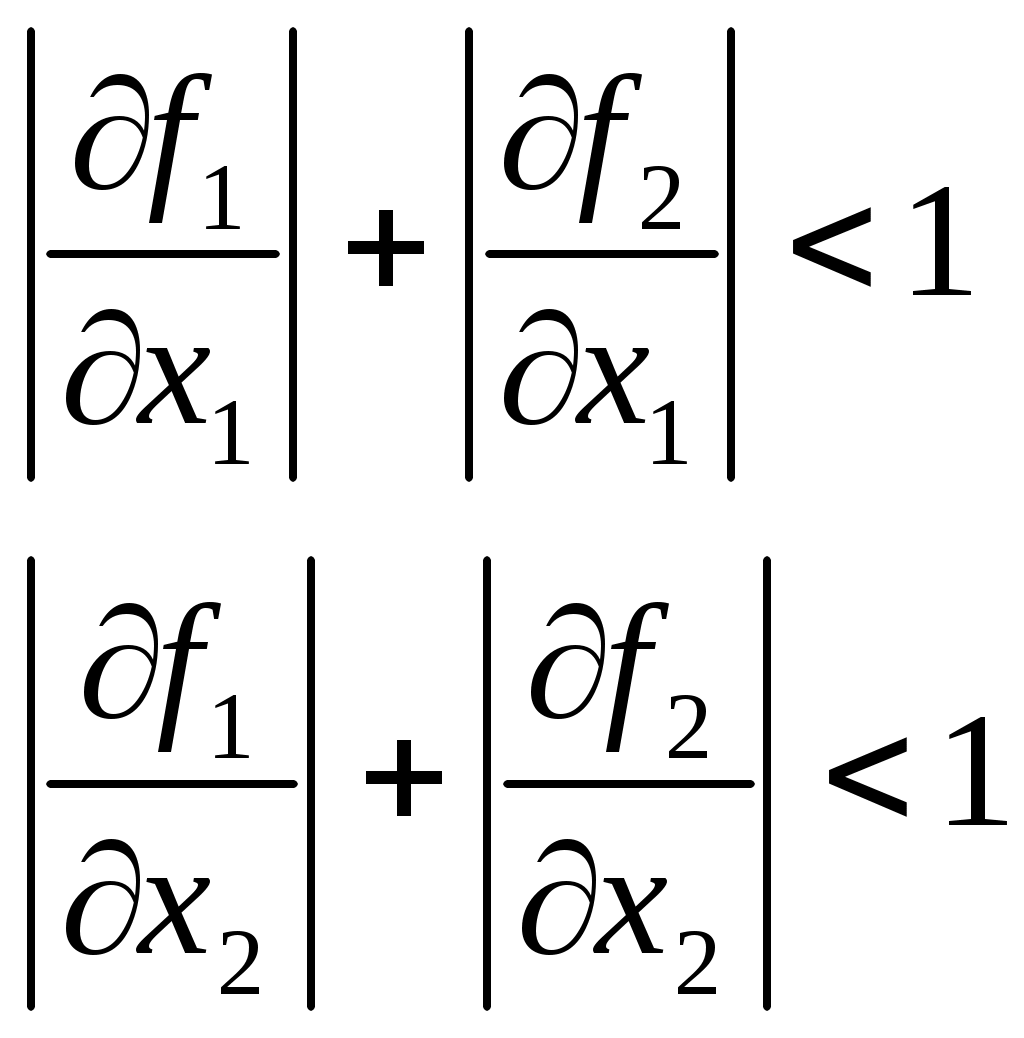 верно верно
|
Тема 6. Численное решение обыкновенных дифференциальных уравнений 1 порядка
№
вопроса
|
Вопросы
|
Варианты ответов
|
1
|
Если последовательные значения функции, являющейся решением задачи Коши для дифференциального уравнения y' = y + x с начальными условиями y'(х0) = y0 и х = х0, находятся по методу Эйлера с шагом 0,1, то y1 равно ….
|
1. 0,1 y0.
2. y0 + 0,1 х0.
3. 1,1 y0 + 0,1 х0.
4. 1,1 y0.
|
2
|
какой метод решения заключается в замене первой производной в уравнении y’(x)=f(x,y) ее аппроксимацией
|
метод Эйлера
|
3.
|
Если последовательные значения функции, являющейся решением задачи Коши для дифференциального уравнения y' = y + 2x
с начальными условиями y'(х0) = y0 и х = х0, находятся по методу Эйлера с шагом 0,1, то y1 равно ….
|
1. 0,2 y0.
2. y0 + 0,2 х0.
3. 1,2 y0.
4. 1,1 y0 + 0,2 х0.
|
4.
|
Методом Эйлера найдите решение дифференциального уравнения y'=xy-2 в точке x=0,1. Начальное условие y(0)=4.
Величина шага h=0.1
|
1. 3.50
2. 3.80
3. 4.21
4. 3.64
|
5
|
для численно решения задачи Коши для ОДУ удобно применение
|
Метода разложения в ряд
Метода Ренге-Кутты
Метода Гаусса
Формулы прямоугольников
|
6
|
Функция системы Mathcad odesolve предназначена для нахождения
|
Приближенного значения корня нелинейного уравнения
Решения обыкновенного дифференциального уравнения
Решения дифференциального уравнения в частных производных
Приближенного значения определенного интеграла
|
7
|
Количество аргументов у функции odesolve
|
1
2
3
4
|
8
|
Функция системы Mathcad rkfixed предназначена для нахождения
|
Приближенного значения корня нелинейного уравнения
Решения обыкновенного дифференциального уравнения
Решения дифференциального уравнения в частных производных
Приближенного значения определенного интеграла
|
9
|
C использованием функции rkfixed системы Mathcad нельзя получить
|
Решения обыкновенного дифференциального уравнения 1 порядка
Решения обыкновенного дифференциального уравнения 2 порядка
Решения обыкновенного системы двух дифференциальных уравнений 1 порядка
Решения дифференциального уравнения в частных производных
|
10
|
C использованием функции rkfixed системы Mathcad нельзя получить
|
Решение задачи Коши обыкновенного дифференциального уравнения 1 порядка
Решения задачи Коши обыкновенного дифференциального уравнения 2 порядка
Решение краевой задачи обыкновенного дифференциального уравнения 2 порядка
Решения дифференциального уравнения в частных производных
|
11
|
Для численного решения обыкновенного дифференциального уравнения 1 порядка применяют метод
|
Ньютона
Гаусса
Эйлера
Коши
|
12
|
Для численного решения обыкновенного дифференциального уравнения 1 порядка применяют метод
|
Ньютона
Гаусса
Рунге-Кутты
Коши
|
13
|
а) формула Эйлера (Рунге-Кутты) для численного решения обыкновенного дифференциального уравнения 1 порядка имеет вид
|
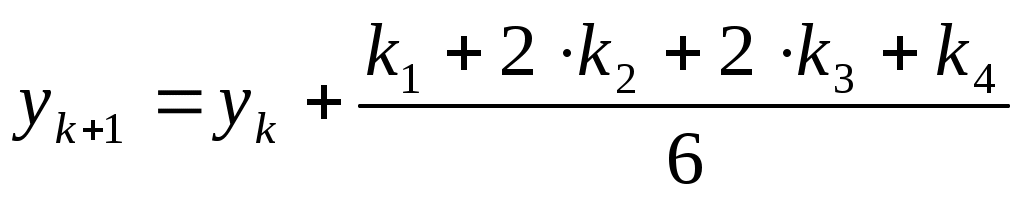 (верно) (верно)
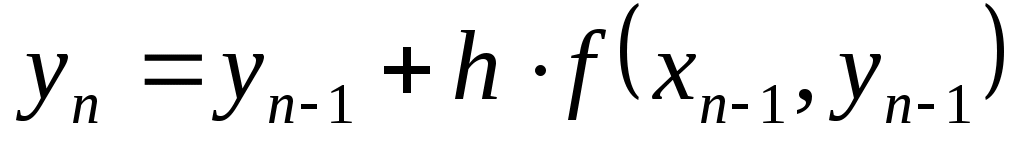 верно верно
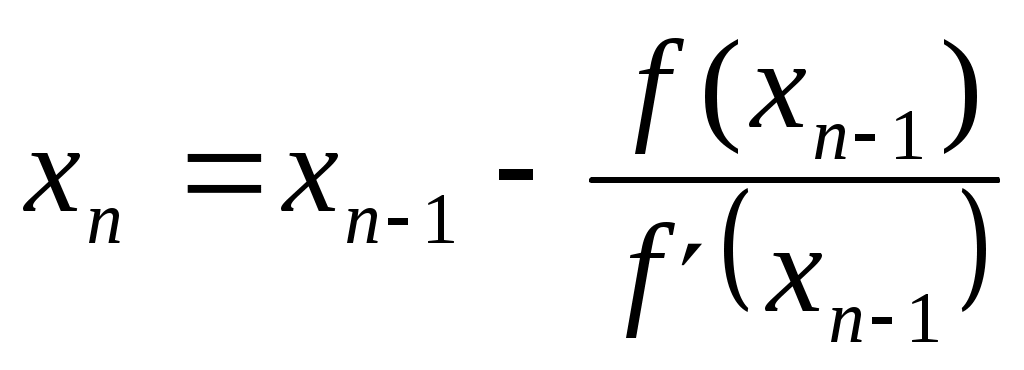
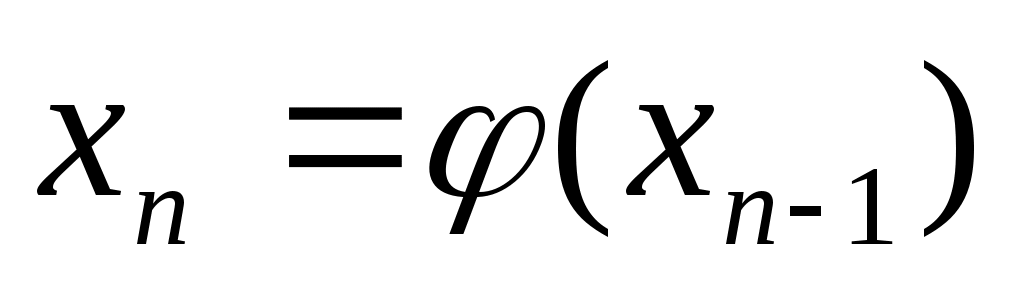
|
14
|
В чем состоит идея метода Рунге-Кутты
|
В том, что приближенное значение на следующем шаге вычисляется в некоторой промежуточной точке, затем усредняется
|
Тема 7. Численное решение систем обыкновенных дифференциальных уравнений 1 порядка
№
вопроса
|
Вопросы
|
Варианты ответов
|
|
|
|
1.
|
Методом Эйлера найдите решение дифференциального уравнения y'=xy-2 в точке x=0,1. Начальное условие y(0)=2.
Величина шага h=0.1
|
1. 1,7.
2. 1,8.
3. 1,9.
4. 2,0.
|
2
|
Для численного решения системы двух обыкновенных дифференциальных уравнений 1 порядка используют метод
|
Итерации
Аппроксимации
Эйлера
прогонки
|
3
|
Если последовательные значения функции, являющейся решением задачи Коши для дифференциального уравнения y' = y - x с начальными условиями y'(х0) = y0 и х = х0, находятся по методу Эйлера с шагом 0,1, то y1 равно ….
|
1. 1,1 y0 - 0,1 х0.
2. y0 + 0,1 х0.
3. 0,1 y0.
4. 1,1 y0.
|
Тема 8. Численное решение обыкновенных дифференциальных уравнений 2 порядка. Задача Коши
№
вопроса
|
Вопросы
|
Варианты ответов
|
|
Для численного решения краевых задач для обыкновенного дифференциального уравнений 2 порядка используют метод
|
Эйлера
Рунге-Кутты
Прогонки
Конечных разностей
|
Тема 9. Численное решение обыкновенных дифференциальных уравнений 2 порядка. Краевая задача
№
вопроса
|
Вопросы
|
Варианты ответов
|
1
|
Не определена краевая задача
|
Первого рода
Второго рода
Третьего рода
Четвертого рода
|
2
|
метод конечных разностей основывается на понятии
|
Определенного интеграла
Производной
|
Тема 10. Численное решение дифференциальных уравнений в частных производных 2 порядка
№
вопроса
|
Вопросы
|
Варианты ответов
|
1
|
Функция системы Mathcad рdesolve предназначена для нахождения
|
Приближенного значения корня нелинейного уравнения
Решения обыкновенного дифференциального уравнения
Решения дифференциального уравнения в частных производных
Приближенного значения определенного интеграла
|
2
|
Количество аргументов у функции рdesolve
|
1
2
3
4
|
3
|
что является основным объектом изучения в математической физике
|
краевая задача
|
4
|
какими условиями дополняются дифференциальные уравнения при описании физических явлений в математической физике
|
Краевые условия
| |
 Скачать 269 Kb.
Скачать 269 Kb.
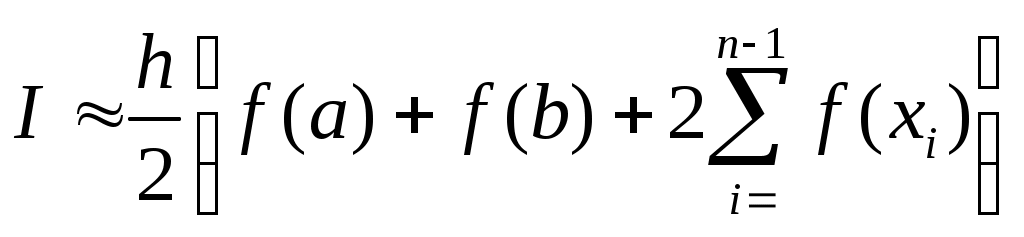
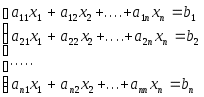
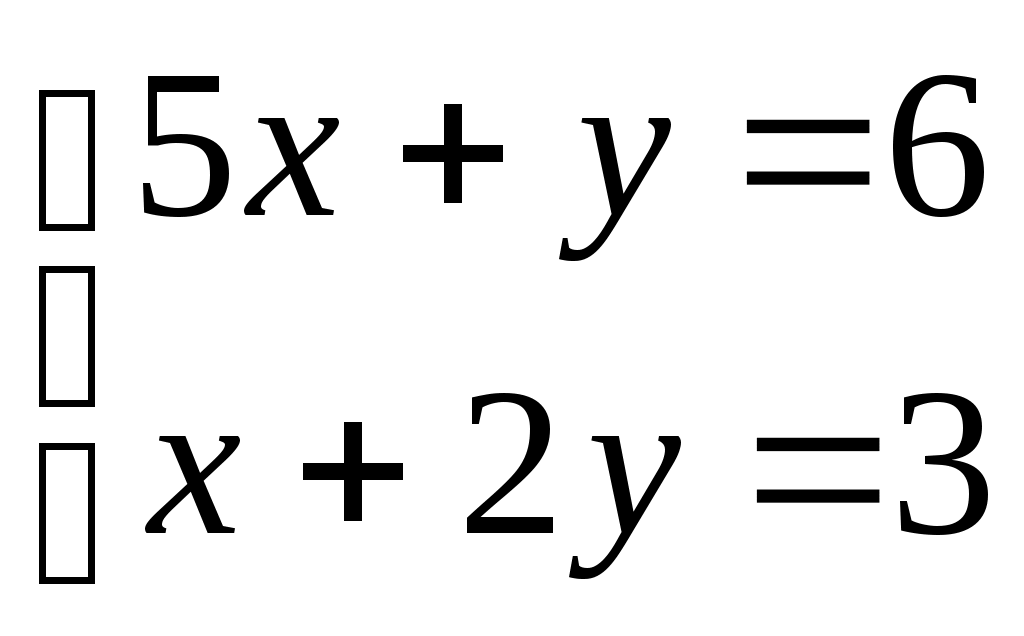 при x0=2 y0=1
при x0=2 y0=1 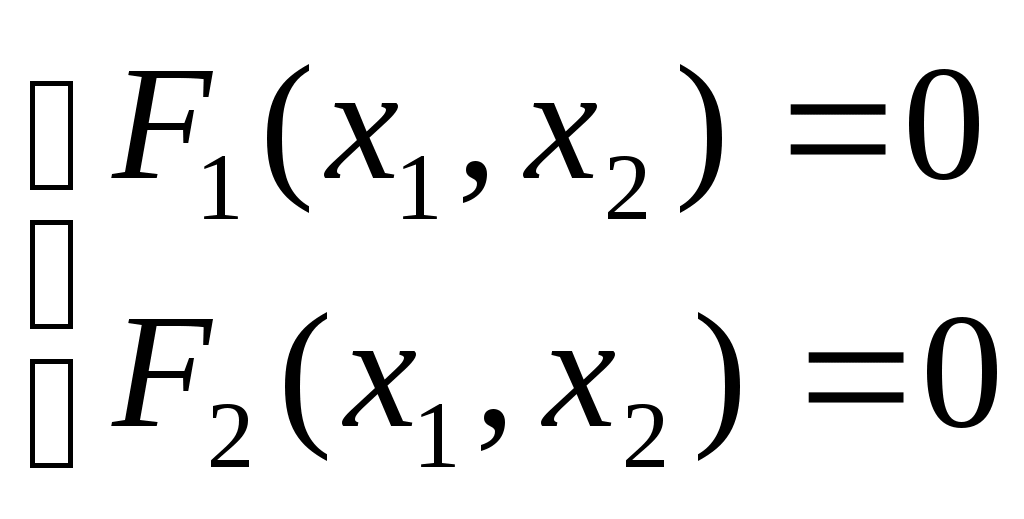 является условие
является условие 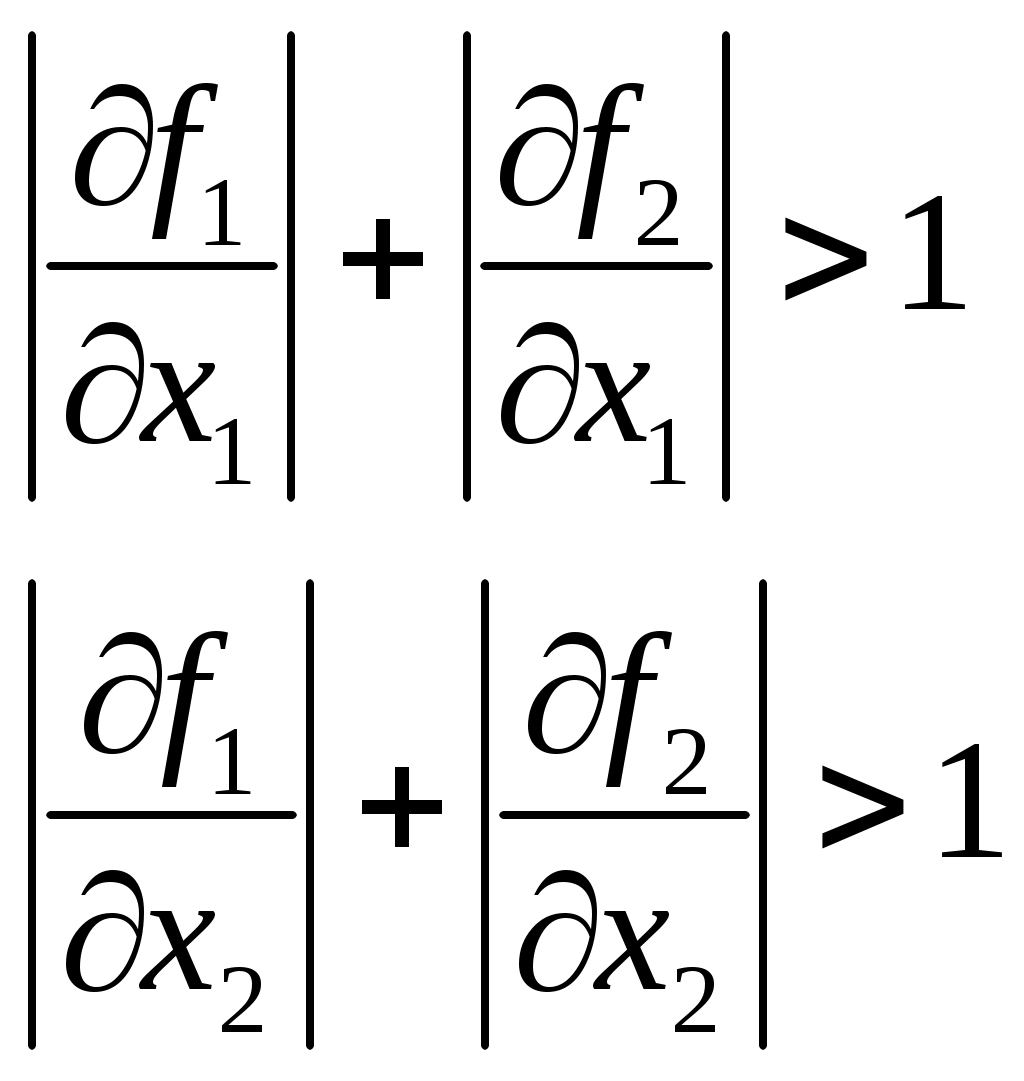
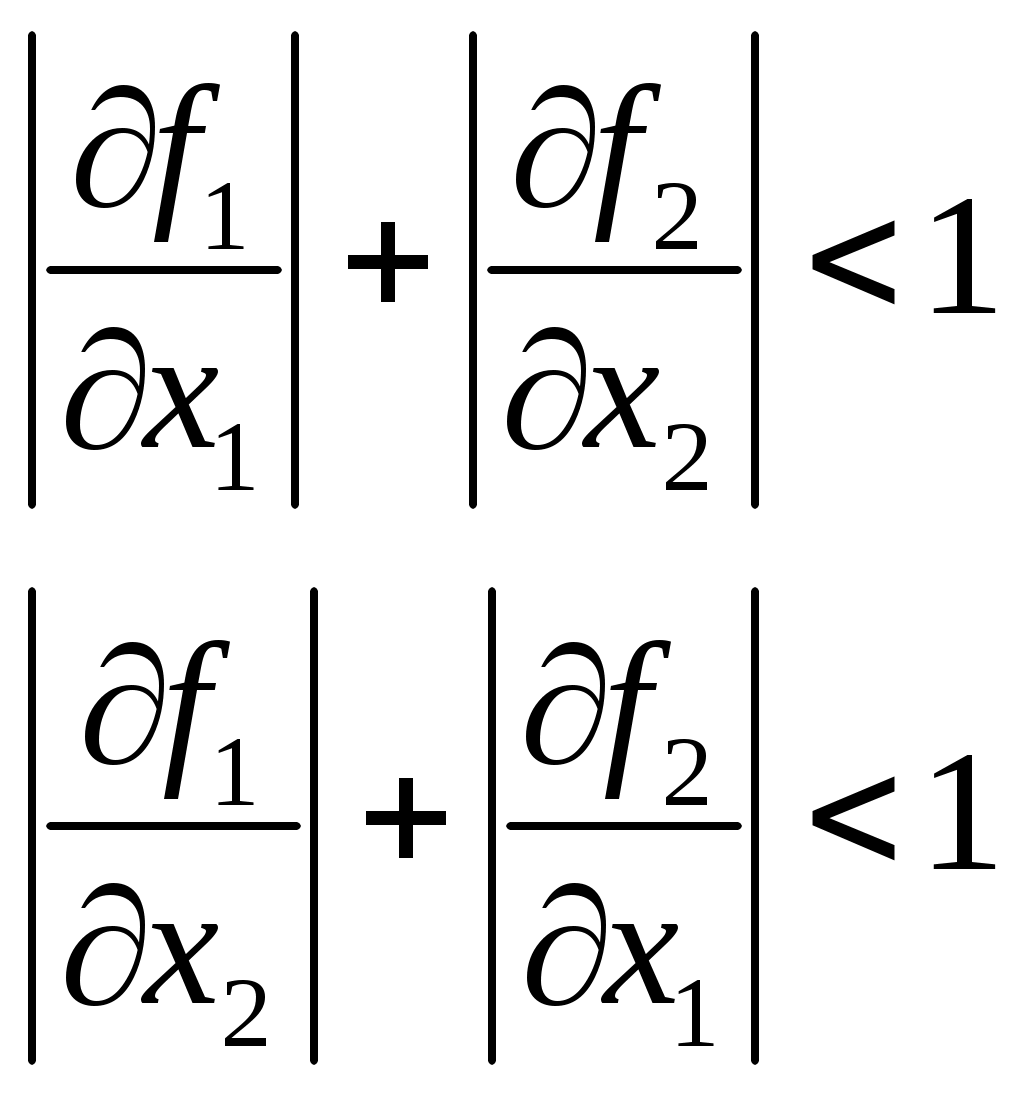
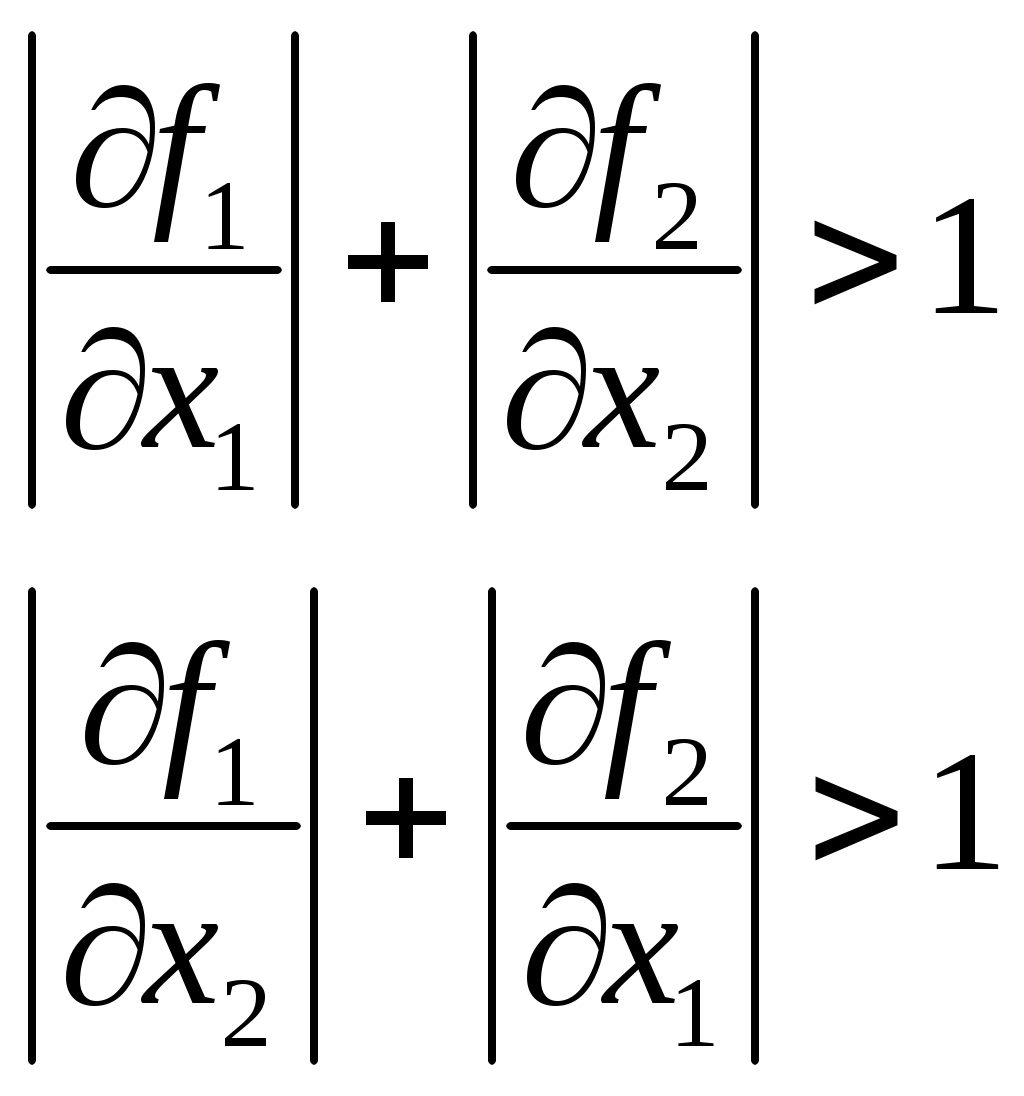
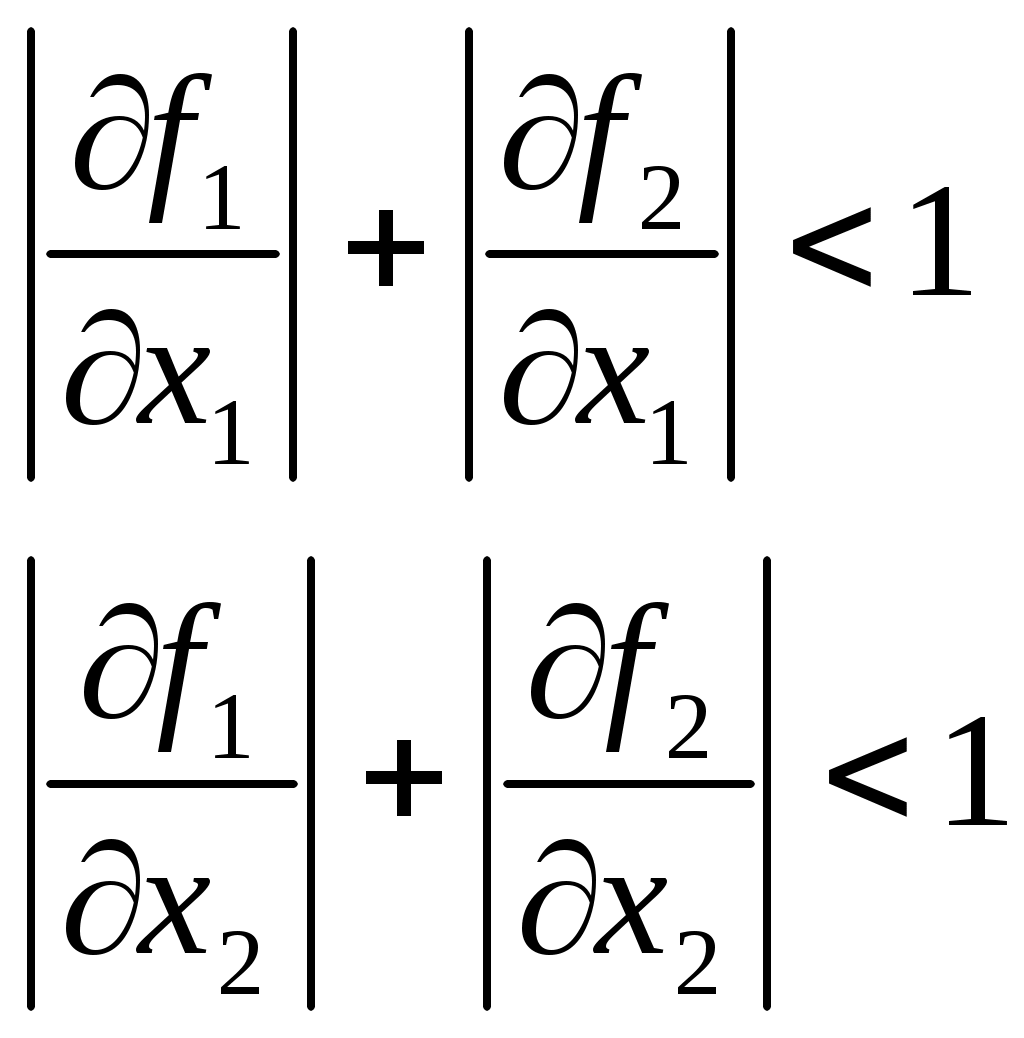 верно
верно