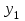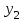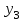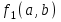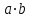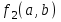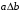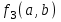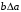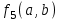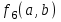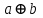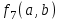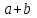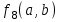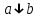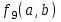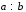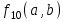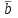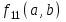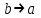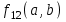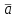БУЛЕВЫ ФУНКЦИИ (2). Булевы функции
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
БУЛЕВЫ ФУНКЦИИ. В отличие от функций непрерывной математики в алгебре логики рассматривают функции, в которых и аргументы и значения функции принимают значения из множества {0,1}. Эти функции называют булевыми функциями. Значения аргументов в дальнейшем будем называть набором аргументов или просто набором. Из определения булевой функции 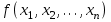 следует, что для ее задания достаточно указать значение функции для каждого набора аргументов, т.е. записать таблицу. следует, что для ее задания достаточно указать значение функции для каждого набора аргументов, т.е. записать таблицу.Число строк таблицы определяется числом возможных наборов аргументов и равно 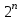 , где , где 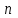 - число аргументов. - число аргументов. Если две функции 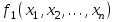 и и 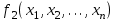 принимают на всех возможных наборах аргументов одинаковые значения, то функции принимают на всех возможных наборах аргументов одинаковые значения, то функции 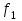 и и 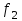 называют равными. называют равными.Функция 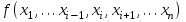 существенно зависит от аргумента существенно зависит от аргумента 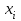 , если имеет место неравенство , если имеет место неравенство 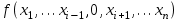 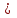 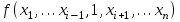 . В противном случае . В противном случае 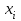 является фиктивным аргументом и его можно удалить. является фиктивным аргументом и его можно удалить.Доказано, что число всех функций, зависящих от 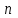 аргументов конечно и равно аргументов конечно и равно 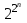 . .Рассмотрим функции одного аргумента 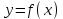 . Столбец . Столбец  - это значение аргумента, а столбцы - это значение аргумента, а столбцы 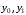
 Функция Функция 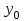 равна нулю при любом значении аргумента и называется константой ноль. Записывается равна нулю при любом значении аргумента и называется константой ноль. Записывается 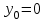 . В дискретных устройствах логический ноль реализуется низким уровнем напряжения: . В дискретных устройствах логический ноль реализуется низким уровнем напряжения: Значения функции 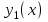 совпадает со значением аргумента, поэтому она называется аргумент x. Обозначается совпадает со значением аргумента, поэтому она называется аргумент x. Обозначается 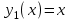 Значения функции 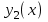 противоположны значению аргумента. Эта функция называется инверсией аргумента x, иногда ее называют НЕ- противоположны значению аргумента. Эта функция называется инверсией аргумента x, иногда ее называют НЕ- . Обозначается . Обозначается 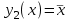 . .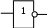 В цифровых устройствах эта функция реализуется логическим элементом, который называется инвертором: В цифровых устройствах эта функция реализуется логическим элементом, который называется инвертором: Значения функции 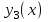 всегда равны единице. Она называется константой единица. Обозначается всегда равны единице. Она называется константой единица. Обозначается 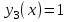 и реализуется высоким уровнем напряжения: и реализуется высоким уровнем напряжения:  +E +E Для двух аргументов существует уже 16 булевых функций.
Среди этих функций следует особо выделить функции конъюнкции, дизъюнкции, Шеффера, Пирса, суммы по модулю 2: -конъюнкция 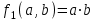 . Эту функцию иногда называют логическим произведением, либо функцией И. В литературе можно встретить различные обозначения этой функции: . Эту функцию иногда называют логическим произведением, либо функцией И. В литературе можно встретить различные обозначения этой функции: 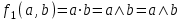 . . -дизъюнкция 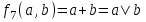 . Эта функция также имеет другие названия: логическое сложение, операция ИЛИ. . Эта функция также имеет другие названия: логическое сложение, операция ИЛИ.-операция Шеффера (штрих Шеффера, функция Шеффера, И-НЕ) 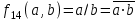 . .-операция Пирса (стрелка Пирса, функция Пирса, ИЛИ-НЕ) 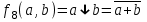 . .-сумма по модулю 2 (исключающее ИЛИ) 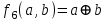 . .В дискретных устройствах эти функции реализуются логическими элементами И, ИЛИ, И-НЕ, ИЛИ-НЕ и элементом сумма по модулю 2. 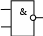    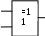 И ИЛИ И-НЕ ИЛИ-НЕ Сумма по mod 2 Рассмотренные функции позволяют строить новые функции путем перестановки аргументов и путем подстановки в функцию новых функций вместо аргументов. Функцию, полученную из функций 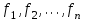 путем применения этих правил называют суперпозицией функций путем применения этих правил называют суперпозицией функций 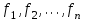 . .При дальнейшем увеличении числа аргументов количество функций быстро возрастает: при 3 аргументах существует 256 функций, при 4 аргументах – 65536 функций,… Среди этих функций есть и уже известные функции 0, 1, 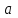 , , 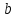 , , 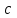 , , 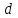 ,…, а также многоместные функции конъюнкции, дизъюнкции, Шеффера и Пирса. При любом числе аргументов для этих функций справедливо следующее: ,…, а также многоместные функции конъюнкции, дизъюнкции, Шеффера и Пирса. При любом числе аргументов для этих функций справедливо следующее:- конъюнкция (И). Если хотя бы один аргумент равен 0, то функция равна 0. Функция равна 1, если все аргументы равны 1; - штрих Шеффера (И-НЕ). Если хотя бы один аргумент равен 0, то функция равна 1. Функция равна 0, если все аргументы равны 1; - дизъюнкция (ИЛИ). Если хотя бы один аргумент равен 1, то функция равна 1. Функция равна 0, если все аргументы равны 0; - стрелка Пирса (ИЛИ-НЕ). Если хотя бы один аргумент равен 1, то функция равна 0. Функция равна 1, если все аргументы равны 0. Основные формулы булевой алгебры. Для доказательства формул можно пользоваться табличным методом. При его использовании строятся таблицы истинности для левой и правой частей доказываемого соотношения. Если эти таблицы совпадают, то имеет место тождество. Свойства конъюнкции, дизъюнкции и отрицания. 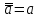 , ,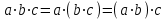 , , 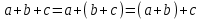 , ,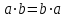 , , 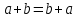 , ,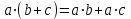 , , 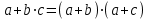 . .Для последнего соотношения нет аналога в обычной алгебре 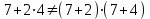 , но в булевой алгебре это тождество. Проверим его справедливость табличным методом: , но в булевой алгебре это тождество. Проверим его справедливость табличным методом:
Пятый и восьмой столбцы соответствуют значениям левой и правой частей на всех возможных наборах аргументов. Совпадение этих столбцов доказывает тождество. Существование последних двух тождеств (распределительных законов) делает законы булевой алгебры полностью двойственными. Это означает, что если существует какое–либо равенство, то существует и второе равенство, в котором символы дизъюнкции заменены символами конъюнкции, а символы конъюнкции – символами дизъюнкции. Пример. Справедливо равенство 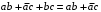 , в силу свойства двойственности справедливо и равенство , в силу свойства двойственности справедливо и равенство 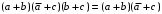 . Эти тождества называются соотношениями Блека – Порецкого. . Эти тождества называются соотношениями Блека – Порецкого. 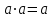 , , 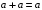 , ,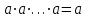 , , 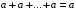 , ,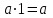 , , 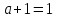 , ,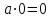 , , 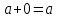 , ,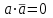 , , 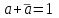 , ,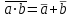 , , 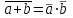 , ,последние два тождества называются правилами де Моргана. Эти правила можно обобщить для нескольких аргументов: 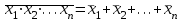 , , 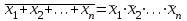 . .Правила поглощения: 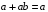 , , 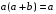 , , , , 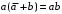 . .Правила склеивания по переменной 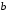 : : 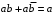 , , 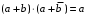 . .Вынесение за скобки: 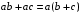 , , 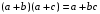 . .Свойства функций Шеффера, Пирса, суммы по модулю 2. 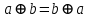 , , 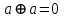 , , 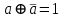 , ,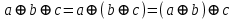 , , 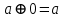 , , 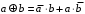 . .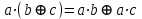 , , 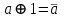 . .Для функций Шеффера и Пирса имеет место переместительный закон: 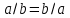 , , 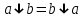 , ,Но сочетательный закон для них НЕ справедлив! 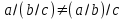 , , 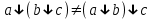 , ,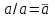 , , 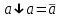 , ,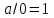 , , 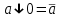 , ,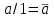 , , 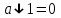 , ,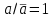 , , 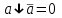 . .Существуют тождества похожие на правила де Моргана: 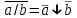 , , 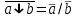 . .На практике часто возникает необходимость преобразовать функцию, аргументы которой связаны операцией Шеффера или Пирса к выражению, содержащему только операции конъюнкции, дизъюнкции и отрицания. Если символы отрицания расположены над одиночными символами переменных, то такая булева функция называется нормальной. Именно такие представления функций наиболее просто воспринимаются человеком. Для подобного преобразования в литературе обычно используют правила де Моргана, однако существует очень простой прием, позволяющий сразу записать искомый результат: 1) заменить в выражении операции Пирса и Шеффера на операции И-НЕ и ИЛИ-НЕ соответственно; 2) подсчитать число инверсий над каждой буквой, если оно четно, то в преобразуемое выражение эта буква будет входить без отрицания, если нечетно – с отрицанием; 3) подсчитать число инверсий над каждой логической операцией, если число инверсий четно, то операция не меняется, если нечетно, то логическая операция заменяется дуальной логической операцией. Пример: 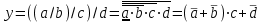 Для функций Шеффера и Пирса можно вывести тождества, похожие на правила склеивания: 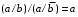 , , 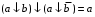 действительно, 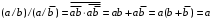 , ,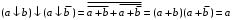 , , |