БУЛЕВЫ ФУНКЦИИ (2). Булевы функции
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
Получение МКНФ и минимальных форм в базисе Пирса. В этих базисах допустимые претенденты ищут, рассматривая матрицу единиц. Рассмотрим алгоритм получения МКНФ. Претендентом служит сумма аргументов взятых с отрицанием или без него. 1) Задать длину претендента 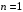 ; ;2) Рассматривая матрицу единиц сформировать очередь всех допустимых претендентов длины  ; ;3) Если очередь пуста, принять 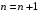 и перейти к пункту 2, иначе – к пункту 4; и перейти к пункту 2, иначе – к пункту 4;4) Взять первого допустимого претендента из очереди и проверить обнуляет ли он хотя бы один набор в матрице нулей. Если – нет, то допустимый претендент удалить из очереди и перейти к пункту 3, если – да, то перейти к пункту 5. 5) Включить допустимый претендент в формулу, представляющую собой произведение претендентов; 6) Исключить наборы матрицы нулей, на которых допустимый претендент равен нулю; 7) Исключить претендент из очереди; 8) Если матрица нулей не пуста, то перейти к пункту 3, иначе – конец. Рассмотрим получение МДНФ той же функции:  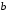  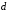  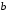  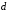 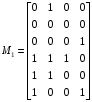 , , 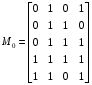 Претенденты 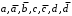 недопустимы, потому что обращают в нуль хотя бы один набор матрицы единиц. недопустимы, потому что обращают в нуль хотя бы один набор матрицы единиц.Из претендентов длины 2 в очередь допустимых претендентов входят 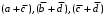 . Допустимый претендент . Допустимый претендент 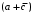 равен нулю на наборах 0101 и 0110 матрицы нулей, поэтому он входит в МКНФ: равен нулю на наборах 0101 и 0110 матрицы нулей, поэтому он входит в МКНФ: 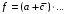 . После исключения наборов 0101, 0110, 0111 получим: . После исключения наборов 0101, 0110, 0111 получим: 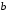  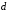  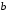  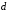 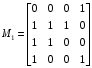 , , 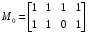 . Следующий допустимый претендент из очереди . Следующий допустимый претендент из очереди 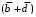 равен нулю на наборах 1111 и 1101 матрицы нулей, т.е. входит в МКНФ: равен нулю на наборах 1111 и 1101 матрицы нулей, т.е. входит в МКНФ: 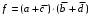 . Т.к. после удаления наборов матрица нулей пуста – минимизация закончена. . Т.к. после удаления наборов матрица нулей пуста – минимизация закончена.Замечание: если искать допустимые претенденты в виде функции Пирса с минимальным числом аргументов, которые равны нулю хотя бы на одном наборе матрицы нулей и равны единице на всех наборах матрицы единиц, то получим минимальную форму в базисе Пирса. Естественно, что следует учитывать особенности этой функции: - если претендент, равный нулю на наборе матрицы нулей и равный единице на всех наборах матрицы единиц состоит из одного аргумента, он должен записываться в минимальную форму с дополнительным отрицанием; - если претендент равен нулю на всех наборах матрицы нулей и равен единице на всех наборах матрицы единиц, то он записывается с общим отрицанием. Для рассмотренного примера допустимые претенденты, которые входят в минимальную форму: 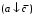 , , 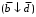 , а минимальное выражение , а минимальное выражение 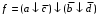 . .Замечание. При минимизации функций большого числа аргументов, матрицы единиц и нулей занимают значительный объем памяти ЭВМ. При большом числе аргументов его можно уменьшить более чем на порядок, если применить следующий прием: для минимизируемой функции выделяются две матрицы размером 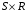 , ,где 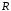 - число разрядов в машинном слове; - число разрядов в машинном слове;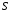 - выделенное число слов. - выделенное число слов.Число слов матрицы при минимизации функции  аргументов определяется по формуле: аргументов определяется по формуле: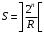 , где , где 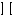 -символ округления результата к большему целому. Номер набора в матрице определяется его положением: -символ округления результата к большему целому. Номер набора в матрице определяется его положением: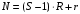 , где , где 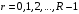 - номер разряда в слове. - номер разряда в слове.Пример: в гипотетической четырехразрядной машине задана матрица Разряд 3 2 1 0 Слово 0 0 0 0 1 Слово 1 0 1 1 0 Слово 2 1 0 0 0 Слово 3 1 0 0 1 Единицы этой матрицы соответствуют наборам 0,5,6,10,11,12,15. Минимизируемую функцию задают двумя подобными матрицами. Исходно эти матрицы заполняются нулями. Затем в матрицу единиц вписывают единицы в позиции, которые соответствуют наборам на которых функция равна единице, а в матрицу нулей вписывают единицы в позиции, которые соответствуют наборам на которых функция равна нулю. Пример: 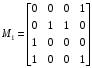 , , 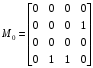 . .Эти матрицы задают не полностью определенную функцию равную единице на наборах 0,5,6,11,12,15 и нулю на наборах 4,13,14. Нетрудно подсчитать, что число слов в каждой из матриц при минимизации функций 32 аргументов на 32-разрядных машинах составит 134217728. Такой объем оперативной памяти доступен для современных ЭВМ. Главными ограничениями метода являются приемлемое время ввода значений функции и время собственно минимизации функции. Однако не следует смотреть на проблему минимизации слишком пессимистично, т.к. известно, что реальные булевы функции большого числа аргументов в подавляющем большинстве случаев не определены, причем число неопределенных наборов возрастает с ростом числа аргументов булевой функции. Синтез комбинационных схем. Существует класс логических устройств, у которых выходные сигналы схемы в данный момент времени зависят только от комбинации входных сигналов поступивших на схему в данный момент времени: 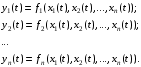 Такие схемы называют комбинационными. Они описываются системой булевых функций. Задача синтеза обратна задаче анализа. Для решения задачи синтеза схема должна быть представлена так называемым техническим заданием. В этом задании, каким – либо способом формулируют основные технические требования, предъявляемые к устройству. Обычно это текстовое описание, при необходимости сдобренное таблицами, графиками, формулами и.т.п. В нем иногда отражают типы логических элементов, на которых реализуется устройство. Как правило, это задание неоднозначно описывает это устройство и поэтому первым шагом синтеза является построение математической модели устройства, в которой эти неоднозначности исключены. Это трудно формализуемый этап, поэтому эту задачу обычно решают самые квалифицированные сотрудники коллектива разработчиков. Если синтезируется комбинационная схема, то последующие этапы это - упрощение математической модели (минимизация системы булевых функций в заданном базисе); - построение функциональной схемы устройства; - преобразование функциональной схемы в принципиальную схему. (Это преобразование Вы сможете проводить после изучения курса «Схемотехника»). Задача. Разработать схему одноразрядного двоичного сумматора. При реализации схемы использовать элементы И-НЕ.  Попытаемся составить математическую модель устройства. Это устройство явно принадлежит к классу комбинационных схем, т.к. сумма определяется значением слагаемых. Определимся с числом входов и выходов схемы: Попытаемся составить математическую модель устройства. Это устройство явно принадлежит к классу комбинационных схем, т.к. сумма определяется значением слагаемых. Определимся с числом входов и выходов схемы:Зачем нужен одноразрядный сумматор? Очевидно для изготовления многоразрядного сумматора. Но при суммировании многоразрядных слов необходимо учитывать перенос из предыдущего младшего разряда, поэтому входов должно быть три: на два входа 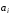 и и 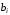 подаются разряды слагаемых, а на третий вход подаются разряды слагаемых, а на третий вход 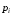 – перенос из предыдущего разряда. Выходов у схемы два, на выходе – перенос из предыдущего разряда. Выходов у схемы два, на выходе 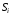 формируется значение суммы в данном разряде, а на выходе формируется значение суммы в данном разряде, а на выходе 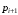 – значение переноса в следующий разряд. Зная правила двоичной арифметики, составляем таблицы истинности этих функций: – значение переноса в следующий разряд. Зная правила двоичной арифметики, составляем таблицы истинности этих функций:
Минимизируем эти функции в базисе Шеффера (И-НЕ): 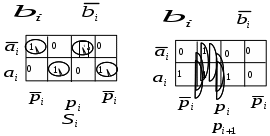 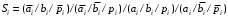 ; ;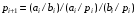 . .Достаточно часто при изображении схем используют так называемый жгут. Жгут – это изображение множества проводников одной жирной линией. Естественно, что провода входящие в жгут и выходящие из него должны маркироваться. Изобразим функциональную схему одноразрядного сумматора: 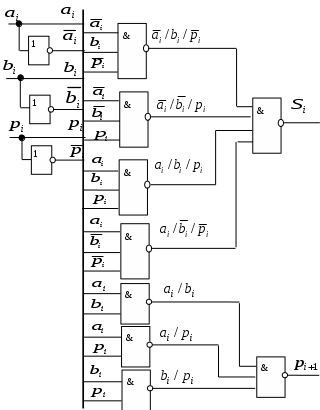 Самостоятельно получите минимальные выражения для этих функций в булевом базисе в дизъюнктивной форме, в булевом базисе в конъюнктивной форме, в базисе Пирса (ИЛИ-НЕ) и начертите схему сумматора в каждом из этих базисов. |
