задача 3 надежность. Решение Метод минимальных сечений

• Название: Решение Метод минимальных сечений
• Анкор: задача 3 надежность
• Дата: 12.10.2022
• Размер: 41.13 Kb.
• Имя файла: 123.docx
• Тип: Решение; #729719

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

3. Мостиковая система

Задание: рассчитать вероятность безотказной работы мажоритарной системы методами: Минимальных сечений, минимальных путей, разложения относительно особого элемента.

Исходные данные: вероятность безотказной работы элементов p=1-0,01*N=1-0,01*21=1-0,12=0,79



Решение:

1. 
   Метод минимальных сечений.
   

Метод минимальных сечений – определение неработоспособности системы при минимальном количестве неработающих элементов.

Минимальное сечение – это набор элементов, отказ которого приводит к отказу системы



Рэ= (1-(1-Р)²)³=(1-(1-0,79)²)³=0,8734

2. 
   Метод минимальных путей
   

Метод минимальных путей – при минимальном количестве работоспособных элементов.

Минимальный путь – последовательный набор элементов, работоспособность которого обеспечивает работоспособность всей системы



P_Э=1-(1-Р₁·Р₂·P₃)·(1-Р₄·Р₅·P₆)·(1-Р₁·Р₇·P₅·P₆)·(1-Р₄·Р₇·P₂·P₃)·(1-Р₁·Р₂·P₈·P₆)·(1-Р₄·Р₅·P₈·P₃)·(1-Р₁·Р₇·P₅·P₈·P₃)· (1-Р₄·Р₇·P₂·P₈·P₆)

Рэ = 1-(1-Р³)²*(1-Р⁴)⁴=1-(1-0,79³)²*(1-0,79⁴)⁴=0,9642

3. Метод разложения относительно особого элемента

P=P_iP_jP(p_i=1, p_j=1)+ P_iq_jP(p_i=1, p_j=0)+ q_iP_jP(p_i=0, p_j=1)+ q_iq_jP(p_i=0, p_j=0).

1) P(p_i=1, p_j=1)

Рэ=(1-(1-Р)²)³=(1-(1-0,79)²)³=0,8734



2) P(p_i=1, p_j=0)

Р₁=1-(1-Р)²=1-(1-0,79)²=0,9559

Р₂=1-(1-Р²)²=1-(1-0,79²)²=0,8586

Рэ=Р₁*Р₂=0,9559*0.8586=0,817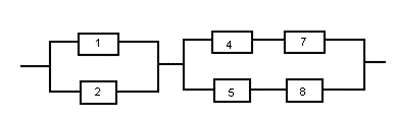



P(p_i=0, p_j=1)

Р₁=1-(1-Р²)²=1-(1-0,79²)²=0.8586

Р₂=1-(1-Р)²=1-(1-0,79)²=0,9559

Рэ=Р₁*Р₂=0.8586*0,9559=0,817



3) P(p_i=0, p_j=0)

Рэ=1-(1-Р³)²=1-(1-0,79³)²=0,7429

Р = 0,79*0,79*0,8734+2*0,79*0,21*0,817+0,21*0,21*0,7429=0.85



Вывод: сравнив 3 метода определили, что наиболее точным является метод минимальных путей, т.к. он рассматривает все варианты функционирования системы.