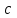БУЛЕВЫ ФУНКЦИИ (2). Булевы функции
 Скачать 2.35 Mb. Скачать 2.35 Mb.
|
|
Мультиплексоры. Проведем анализ еще одной простейшей схемы, которую называют мультиплексором:  Запишем уравнение для выходного сигнала мультиплексора:  . Функция зависит от шести аргументов, поэтому таблица истинности будет слишком громоздкой. Вычислим значения функции . Функция зависит от шести аргументов, поэтому таблица истинности будет слишком громоздкой. Вычислим значения функции  задавая только значения задавая только значения 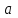 и и 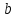 : :
Входы 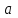 и и 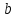 мультиплексора называют адресными, а входы мультиплексора называют адресными, а входы  , , 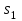 , ,  , ,  -селектируемыми. Из таблицы видно, что мультиплексор подключает к своему выходу один из селектируемых входов, номер которого определяется кодом на адресных шинах. -селектируемыми. Из таблицы видно, что мультиплексор подключает к своему выходу один из селектируемых входов, номер которого определяется кодом на адресных шинах.Число селектируемых входов равно 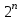 , где , где 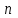 - число адресных входов. - число адресных входов.В литературе тип мультиплексора часто задают обозначением  , здесь , здесь 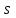 - число селектируемых входов мультиплексора, которые коммутируются на 1 выход. Существуют мультиплексоры 2x1, 4x1, 8x1, 16x1, 32x1 и т.д. Мы рассмотрели мультиплексор 4x1. Принцип работы других мультиплексоров подобен работе мультиплексора 4x1. Например функционирование мультиплексора 8x1 можно пояснить аналогичной таблицей: - число селектируемых входов мультиплексора, которые коммутируются на 1 выход. Существуют мультиплексоры 2x1, 4x1, 8x1, 16x1, 32x1 и т.д. Мы рассмотрели мультиплексор 4x1. Принцип работы других мультиплексоров подобен работе мультиплексора 4x1. Например функционирование мультиплексора 8x1 можно пояснить аналогичной таблицей:
Постройте самостоятельно подобные таблицы для мультиплексоров 2x1 и 16x1. Приведем условные графические обозначения (УГО) некоторых мультиплексоров:   2x 2x1 4x1 Как выглядят УГО мультиплексоров 8x1 и 16x1? Любую булеву функцию можно реализовать с помощью мультиплексора. Для этого аргументы функции подают на адресные входы мультиплексора, а значения функции на соответствующие селектируемые входы. Пример. Реализовать на мультиплексоре функцию:
Не следует думать, что число аргументов реализуемой функции должно быть обязательно равно числу адресных входов мультиплексора. Число аргументов может быть большим, но логика формирования селектируемых сигналов обычно усложняется. Пример: Реализовать на мультиплексоре 4x1 функцию:
Подключим к адресным входам мультиплексора 4x1 два аргумента, например  и и  . При таком подключении сигнал на адресном входе . При таком подключении сигнал на адресном входе 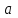 совпадает с совпадает с  , а на входе , а на входе 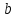 с с  . Поскольку на первых четырех наборах . Поскольку на первых четырех наборах  , то сигнал на выходе мультиплексора совпадает с сигналом на шине , то сигнал на выходе мультиплексора совпадает с сигналом на шине  . Нижняя строчка таблицы на наборах 0, 1, 2, 3 показывает какой сигнал должен формироваться на шине . Нижняя строчка таблицы на наборах 0, 1, 2, 3 показывает какой сигнал должен формироваться на шине  . Эти сигнал не постоянен, следовательно он зависит от еще не учтенных аргументов . Эти сигнал не постоянен, следовательно он зависит от еще не учтенных аргументов  и и  : :  . Легко увидеть, что логика формирования сигнала . Легко увидеть, что логика формирования сигнала  . .Рассуждая аналогично можно найти логику формирования сигналов на остальных селектируемых шинах:  , ,  , ,  . . 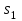      
    Сигнал на  Сигнал на Сигнал на 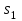 Сигнал на Сигнал на  Сигнал на Сигнал на   Сложность логики, формирующей сигналы на селектируемых входах, зависит от того, какие аргументы подключены к адресным входам. Оптимальную схему можно получить, выполнив синтез для всех возможных комбинаций адресных сигналов. Если брать мультиплексор с числом адресных входов на единицу меньше, чем число аргументов функции, то для реализации функции потребуется мультиплексор и, возможно, один инвертор. Пример: Реализовать функцию заданную таблично
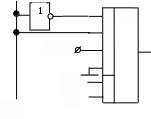 Заметим, что если бы на нулевом наборе функция была бы равна нулю, а на первом наборе – равна единице, инвертор не понадобился бы. |