Дискретная математика. Дискретный матан. Контрольная работа за 3 семестр По дисциплине
 Скачать 90.32 Kb. Скачать 90.32 Kb.
|
y)↓ xz 2. Требуется: а) для функции f (x, y) 1составить таблицу истинности и найти по ней полином Жегалкина, СДНФ, СКНФ. Упростить, если возможно, СДНФ; б) для функции f (x, y,z) 2составить таблицу истинности и найти по ней полином Жегалкина, СДНФ, СКНФ. По карте Карно получить минимальную ДНФ, нарисовать эквивалентную РКС; в) составить таблицу Поста для системы функций f (x, y) 1, f (x, y,z) 2, проверить полноту системы и выбрать базисы, если она полная. Решение. а) Таблица истинности
Полином Жегалкина f (x,y) = ∑ (x + ¬a1)( y + ¬a2) Получим f1(x1,y1) = (x + 1)(y + 1) + (x + 1)y + x(y + 1) = x(y + 1) + (y + 1) + + (x + 1)y + x(y + 1) = (y + 1) + (x + 1)y = y +1+ xy + y =1+ xy СДНФ: f1(x,y) = ¬x * ¬y v ¬x * y v x * ¬y => f1(x,y) = ¬x v x * ¬y СКНФ: f1 (x,y) = ¬x v ¬y б) Таблица истинности
Полином Жегалкина f (x,y,z) = ∑ (x + ¬a1) (y + ¬a2) (z + ¬a3) Тогда получим f1 (x,y,z) = (x + 1)y(z + 1) + x(y + 1)(z + 1) + x(y + 1)z = = (x + 1)y(z + 1) + x(y + 1) = (xyz + yz + xy + y) + (xy + x) = xyz + yz + y + x СНДФ: f2 (x,y,z) = ¬x * y * ¬z v x * ¬y *¬z v x * ¬y *z СКНФ: f (x,y,z) = (x¬a1 v y¬a2 v z¬a3) Получим f (x, y, z) = (x v y v z) * (x v y v ¬z) * (x v ¬y v ¬z) * (¬x v ¬y v z) * *(¬x v ¬y v ¬z) Карта Карно:
в) Для того чтобы система функций была полна, необходимо и достаточно, чтобы она содержала: 1) хотя бы одну функцию, не сохраняющую ноль; 2) хотя бы одну функцию, не сохраняющую единицу; 3) хотя бы одну несамодвойственную функцию; 4) хотя бы одну нелинейную функцию; 5) хотя бы одну немонотонную функцию. Таблица Поста:
Задача 21. Составить для данного графа структурную матрицу. Найти: а) все простые пути из вершины i = 3в вершину j = 1; б) совокупность всех сечений между вершинами iи j. 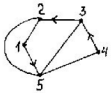 Составим структурную матрицу S = 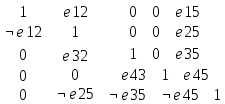 а) Вычеркиваем из матрицы 1-ую строчку и 3-ый столбец, получаем минор M(1,3): M(1,3) = 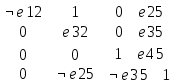 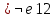 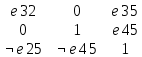 = = = ¬e12 ¬e32 v ¬e12¬e25 ¬e35 v ¬e12¬e32 ¬e45 ¬e45 Задача 31. Заданы сеть и начальный поток f: 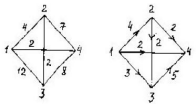 Требуется построить максимальный поток, считая вершину с номером 1 источником и вершину с номером 4 стоком. Указать минимальное сечение, величина которого равна максимальному потоку. Решение. Расставим пометки: 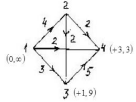 Таким образом, поток можно увеличить на 3 единицы. Получим новый поток, на котором снова расставим пометки: 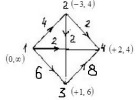 Таким образом, поток можно увеличить на 4 единицы. Получим новый поток, на котором снова расставим пометки: 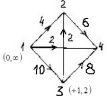 Кроме источника можно пометить только одну вершину. Из множества помеченных вершин в множество непомеченных вершин идут только прямые насыщенные дуги 1-2, 1-4, 3-2, 3-4. Эти три дуги образуют минимальное сечение, величина которого равна 16 единицам, и эта же величина равна величине потока. Таким образом, поток на последнем рисунке является максимальным. Задача 41. На множестве A = {1,2,3,4,5,6} задано отношение делимости: xRy тогда и только тогда, когда x делится на y. Для каждого отношения нужно: а) записать отношение R; б) построить матрицу смежности и граф отношения; в) проверить, является ли отношение рефлексивным, симметричным, транзитивным. Решение. R = 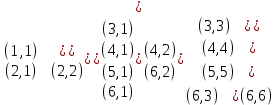 б) Матрица смежности А(¬G) = 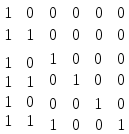 Граф отношения (петли не изображены, отношение - рефлексивное): 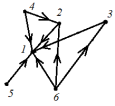 в) проверить, является ли отношение рефлексивным, симметричным, транзитивным. Отношение R: рефлексивно, т.к. ∀a∈ A: aRa; не симметрично, т.к. ∀a,b∈ A: aRb ⇒ bRaне выполняется; транзитивно, т.к. ∀a,b,c∈ A:(aRb)∧(bRc)⇒ aRc . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
