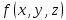Контрольная работа по Дискретной математике (9 вариант, 2 курс). Контрольная работа по курсу Дискретная математика
 Скачать 141.99 Kb. Скачать 141.99 Kb.
|
|
Контрольная работа по курсу «Дискретная математика» Вариант 9 9. Используя правила де Моргана, получить ДНФ и упростить ее 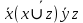 Решение: 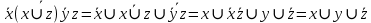 19. Даны две функции f1(x, y), f2(x, y, z). Требуется: а) для функции f1(x, y) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. Упростить, если возможно, СДНФ. б) для функции f2(x, y, z) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. По карте Карно получить минимальную ДНФ, нарисовать эквивалентную РКС. в) составить таблицу Поста для системы функций f1(x, y), f2(x, y, z), проверить полноту системы и выбрать базисы, если она полная. 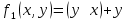 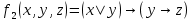 Решение: а) составим таблицу истинности для функции  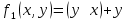
СДНФ – строится на наборах, на которых функция принимает значение 1 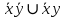 СКНФ – строится на наборах, на которых функция принимает значение 0  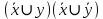 Минимизированная ДНФ  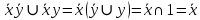 Полином Жегалкина Для n=2 Р(х,у)=а0+а1х+а2у+а3ху f(0,0)=P(0,0)=1= а0+а1*0+а2*0+а3*0= а0, получим а0=1 f(0,1)=P(0,1)=1= а0+а1*0+а2*1+а3*0= 1+а2= 1, получим а2=0 f(1,0)=P(1,0)=0= а0+а1*1+а2*0+а3*0= 1+а1= 0, получим а1=1 f(1,1)=P(1,1)=0= а0+а1*1+а2*1+а3*1= 1+1+а3= 0, получим а3=0 Р(х,у)=1+х – полином Жегалкина б) составим таблицу истинности для функции  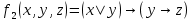
СДНФ – строится на наборах, на которых функция принимает значение 1 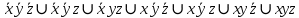 СКНФ – строится на наборах, на которых функция принимает значение 0  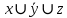 Минимизированная ДНФ 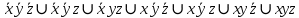 = =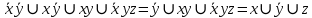 Полином Жегалкина Для n=3 Р(х,у,z)=а0+а1х+а2у+а3z+а4хy+а5уz+а6xz+ а7xyz f(0,0,0)=P(0,0,0)= а0=1, получим а0=1 f(0,0,1)=P(0,0,1)= а0 +а3z= 1 +а3= 1 , получим а3=0 f(0,1,0)=P(0,1,0)= а0 +а2y= 1 +а2= 0 , получим а2=1 f(0,1,1)=P(0,1,1)= а0+а2у+а3z+а5уz=1+1+ а5 = 1 , получим а5=1 f(1,0,0)=P(1,0,0)= а0 +а1x= 1 +а1= 1 , получим а1=0 f(1,0,1)=P(1,0,1)= а0+а1х+а3z+а6xz = 1+ а6= 1 , получим а6=0 f(1,1,0)=P(1,1,0)= а0+а1х+а2у+а4хy=1+1+ а4 = 1 , получим а4=0 f(1,1,1)=P(1,1,1)= а0+а1+а2+а3+а4+а5+а6+а7 = 1+1+1+1+1+а7 = 1 , получим а7=0 Р(х,у,z)=1+y+xy+yz+xyz– полином Жегалкина Найдем минимизированную ДНФ с помощью карт Карно Область 1:
К1: х Область 2:
К2: 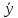 Область 3:
К3: 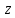 Минимизированная ДНФ:  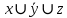 Построим РКС 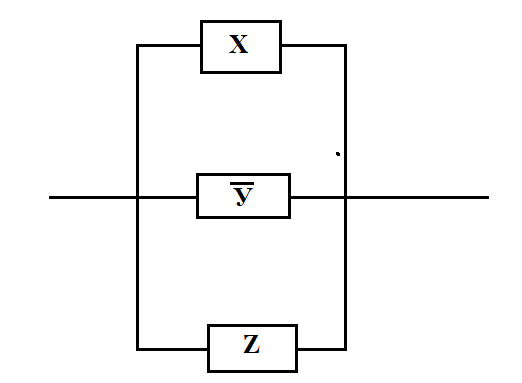 в) таблицы Поста для функции  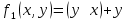 Класс T0 Функция принадлежит классу T0, если на нулевом наборе она сохраняет 0. На нулевом наборе значение функции f(0,0)=1, поэтому функция не принадлежит классу T0. Класс T1 Функция принадлежит классу T1, если на единичном наборе она сохраняет 1. На единичном наборе значение функции f(1,1)=0 поэтому функция не принадлежит классу T1. Класс L Функция принадлежит классу линейных функций (L), если её полином Жегалкина не содержит произведений. Полином Жегалкина функции: 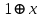 не содержит произведений, поэтому функция принадлежит классу L. не содержит произведений, поэтому функция принадлежит классу L.Класс M Функция принадлежит классу монотонных функций (M), если для любой пары наборов α и β таких, что α ≤ β, выполняется условие f(α) ≤ f(β). Сравним соседние наборы по первой переменной Сравним значения {1} и {1}: условие монотонности выполнено. Сравним значения {0} и {0}: условие монотонности выполнено Сравним соседние наборы по второй переменной Сравним значения {1,1} и {0,0}: условие монотонности нарушено Таким образом функция не принадлежит классу M. Класс S Функция принадлежит классу самодвойственных функций (S), если на противоположных наборах она принимает противоположные значения. Проверим значения на наборах {0, 0} и {1, 1}: 1 и 0 противоположны. Проверим значения на наборах {0, 1} и {1, 0}: 1 и 0 противоположны Поэтому функция принадлежит классу S Построим таблицу
для функции  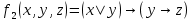 Класс T0 Функция принадлежит классу T0, если на нулевом наборе она сохраняет 0. На нулевом наборе значение функции f(0,0,0)=1, поэтому функция не принадлежит классу T0. Класс T1 Функция принадлежит классу T1, если на единичном наборе она сохраняет 1. На единичном наборе значение функции f(1,1,1)=1 поэтому функция принадлежит классу T1. Класс L Функция принадлежит классу линейных функций (L), если её полином Жегалкина не содержит произведений. Полином Жегалкина функции: Р(х,у,z)=1+y+xy+yz+xyz содержит произведения, поэтому функция не принадлежит классу L. Класс M Функция принадлежит классу монотонных функций (M), если для любой пары наборов α и β таких, что α ≤ β, выполняется условие f(α) ≤ f(β). Сравним соседние наборы по первой переменной Сравним значения {1} и {1}: условие монотонности выполнено. Сравним значения {0} и {1}: условие монотонности выполнено Сравним значения {1} и {1}: условие монотонности выполнено Сравним значения {1} и {1}: условие монотонности выполнено Сравним соседние наборы по второй переменной Сравним значения {1,1} и {0,1}: условие монотонности нарушено Таким образом функция не принадлежит классу M. Класс S Функция принадлежит классу самодвойственных функций (S), если на противоположных наборах она принимает противоположные значения. Проверим значения на наборах {0, 0, 0} и {1, 1, 1}: 1 и 1 совпадают. Поэтому функция не принадлежит классу S Построим таблицу
Получим итоговую таблицу:
В каждом столбце есть « - », следовательно, система полная 29. Дан граф. Составить для данного графа структурную матрицу. Найти: а) все простые пути из вершины i в вершину j; б) совокупность всех сечений между вершинами i и j. 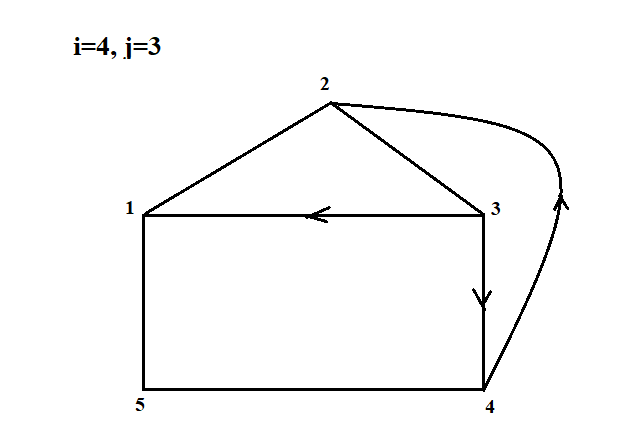 Решение: Граф имеет ориентированные ребра (3,1), (3,4) и (4,2) Структурная матрица S имеет вид: 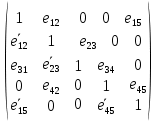 Для получения минора М34 вычеркиваем из матрицы третью строку и четвертый столбец 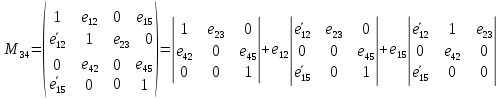 = =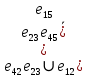 Простые пути из вершины 4 в вершину 3: 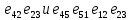 Найдем сечения ( 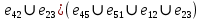 = =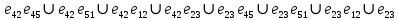 = =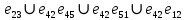 . .39. Задана сеть и начальный поток f. Требуется построить максимальный поток, считая вершину с номером 1 источником и вершину с номером 4 стоком. Указать минимальное сечение, величина которого равна максимальному потоку. 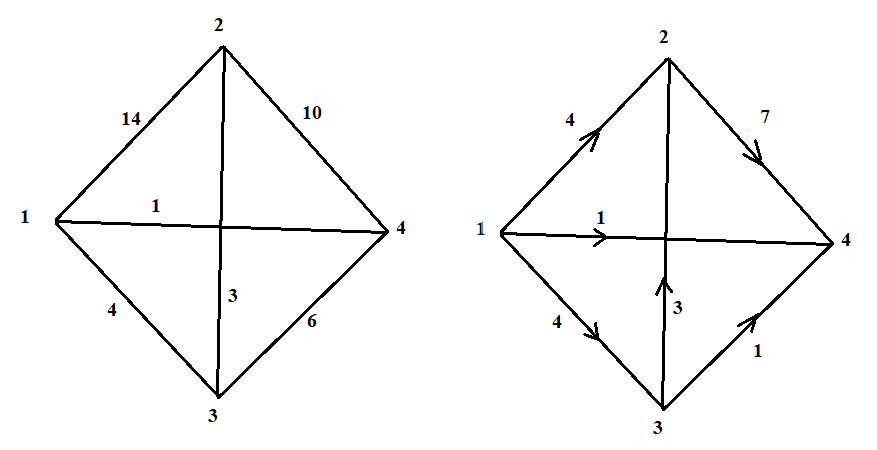 Решение: 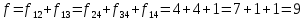 путь из s=1 в t=4 по которому поток может быть увеличен 1-2-4 Пометки вершин s=(0, 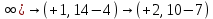 . Добавка к потоку . Добавка к потоку 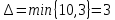 Построим новый поток, увеличенный на 3: 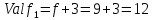 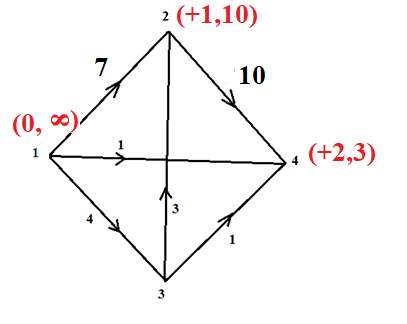 путь из s=1 в t=4 по которому поток может быть увеличен 1-3-4 Пометки вершин s=(0, 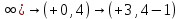 . Добавка к потоку . Добавка к потоку 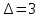 Построим новый поток, увеличенный на 3, при этом, не отправляя по потоку (3,2), а направив в поток (3,4): 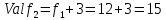 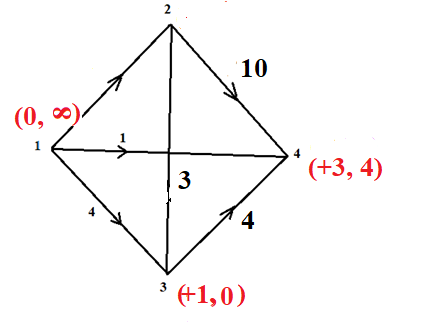 путь из s=1 в t=4 по которому поток может быть увеличен 1-2-3-4 Пометки вершин s=(0, 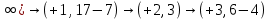 . Добавка к потоку . Добавка к потоку 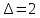 Построим новый поток, увеличенный на 2:  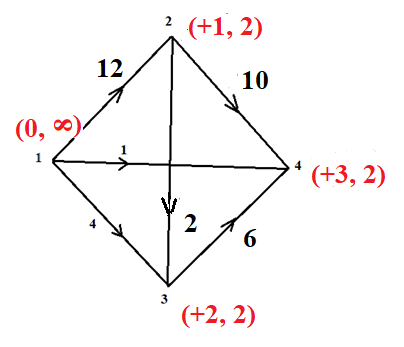 Больше поток увеличить нельзя Дуги (1,4) (2,4), (3,4) – насыщенные Дуги (1,2) и (2,3) ненасыщенные Минимальное сечение 14+3=17 совпадает с величиной максимального потока. 49. На указанном множестве задано отношение. Для отношения нужно: а) записать отношение R; б) построить матрицу смежности и граф отношения; в) проверить, является ли отношение рефлексивным, симметричным, транзитивным. На множестве А={1,2,3,4,5,6} задано отношение R: xRy тогда и только тогда, когда |x-y| нечетное Решение: а) R={(1,2), (2,1), (1,4), (4,1), 1,6), (6,1), (2,3), (3,2), (2,5), (5,2), (3,4), (4,3), (3,6), (6,3), (4,5), (5,4), (5,6), (6,5)} б) построим матрицу смежности  Построим граф отношения: 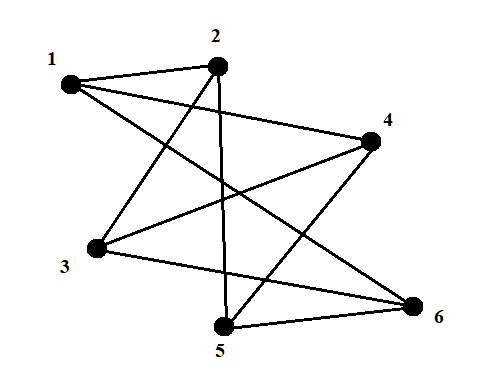 в) отношение не рефлексивно, так как (х, х) 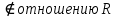 Разность двух одинаковых чисел равна нулю, а ноль – это четное число Отношение симметрично, так как выполняется условие: если xRy, то и уRх, например: если (1, 2) 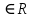 , то и (2, 1) , то и (2, 1) 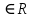 Отношение не транзитивно, так как не выполняется условие, что если xRy, а уRz, то и xRz. Например: (1, 2) 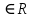 , (2, 5) , (2, 5) 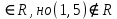 |

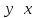
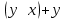
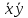
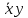
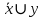
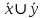
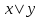
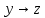
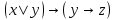
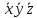
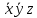
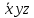
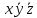
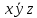
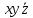
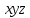
 yz
yz