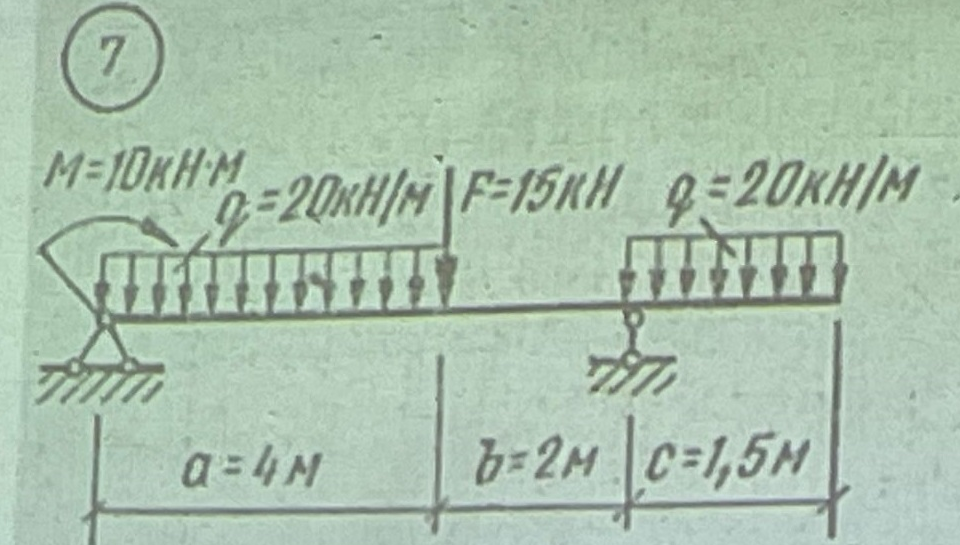
вариант 7- эпюры плюс внизу. Решение y М10кНм f 15кН q20 кНм r b
 Скачать 3.67 Mb.
|
|
Задача 1
Для двухопорной балки построить эпюры изгибающих моментов и поперечных сил. Решение  y М=10кНм  F=15кН q=20кН/м    RB  q=20кН/м    RA z  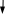 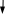 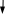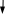А В z1 z2  z3       z01 a=4м b=2м с=1,5м       Эпюра Qy (кН)    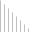  52,92 30  1см    20кН 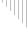      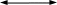 27,08 42,08 42,08 Эпюра Mх (кНм) 22,5 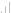      1см     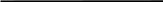 10     40кНм 61,68  80 Условия равновесия балки записываем в виде: сумма моментов всех сил относительно опор А и В равна нулю, сумма проекций на горизонтальную ось равна нулю. В качестве проверки правильности решения используем условие: сумма проекций всех сил на вертикальную ось равна нулю. Так как нет никакой горизонтальной нагрузки, то можно считать, что в опорах А и В возникают реактивные реакции RA и RB перпендикулярные, опорной плоскости. 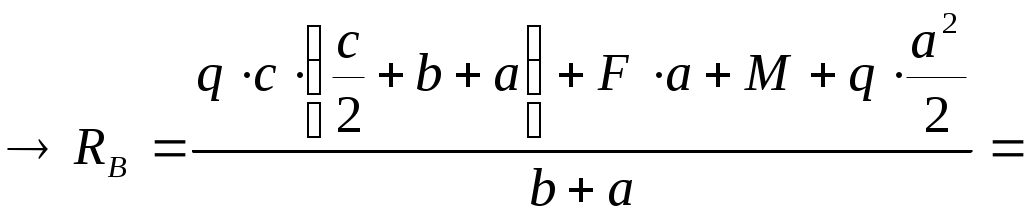  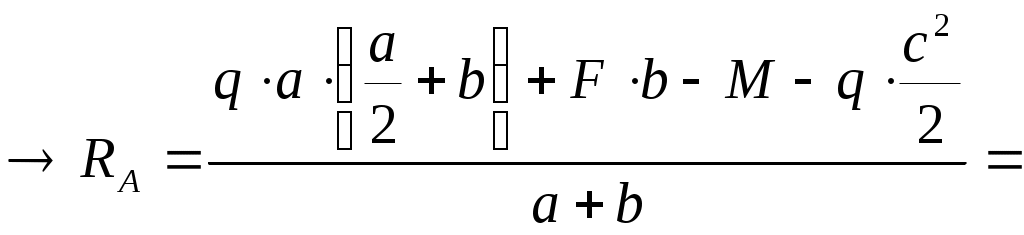 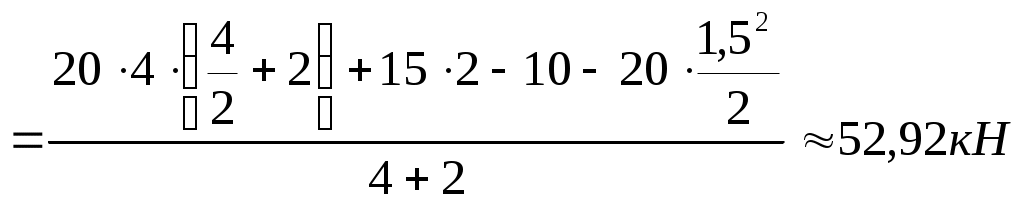   Проверка  - верно.Поперечная сила в сечении балки считается положительной, если равнодействующая внешних сил слева от рассматриваемого сечения направлена снизу вверх, а справа – сверху – вниз, и отрицательной в противоположном случае. Ординаты эпюр поперечных сил соответствующим положительным значениям будем откладывать вверх от оси балки, а отрицательные - вниз. Изгибающий момент считается положительным, если равнодействующий момент внешних сил направлен по часовой стрелке слева от сечения и справа - против часовой стрелки. Ординаты эпюр изгибающих моментов соответствующим положительным значениям будем откладывать вниз от оси балки, а отрицательные – вверх. Р  ассмотрим первый участок. Ход слева.    Эпюра Qу изображается наклонной прямой, и так как на этом участке она меняет знак, то на эпюре моментов будет точка экстремума, расстояние найдем из подобия треугольников :     Эпюра Мx изображается параболической кривой, имеющая точку экстремума и выпуклость которой направлена в сторону распределенной нагрузки:  Рассмотрим второй участок длиной 3м. Ход слева.  Эпюра Qy изображается прямой параллельной оси балки.    Эпюра Мz изображается наклонной прямой.  Рассмотрим третий участок. Ход справа.        Эпюра Мz изображается наклонной прямой. |
