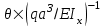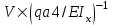Задача 1 Для стержневых систем, изображенных на рис. 57 64, требуется
 Скачать 1.71 Mb. Скачать 1.71 Mb.
|
 Задача 1 Задача 1Для стержневых систем, изображенных на рис. 1.57 – 1.64, требуется: 1.определить опорные реакции, если это необходимо для построения эпюр; 2.установить число участков; 3.применить метод сечений и получить аналитические выражения внутренних силовых факторов по участкам (изобразить графически рассматриваемую часть балки и все действующие на нее силы и моменты); 4.вычислить значения внутренних силовых факторов в характерных точках участка и определить экстремальные их значения; 5.по вычисленным значениям на одном листе с изображением стержневой системы построить эпюры внутренних силовых факторов (графическая часть задания); 6.проверить правильность построения эпюр, пользуясь дифференциальными зависимостями между внутренними силовыми факторами и другими правилами проверки эпюр.  Исходные данные взять из таблицы.
 Намечаем сечения. Определяем поперечные силы и изгибающие моменты в сечениях. Намечаем сечения. Определяем поперечные силы и изгибающие моменты в сечениях. Первое сечение:
Второе сечение:
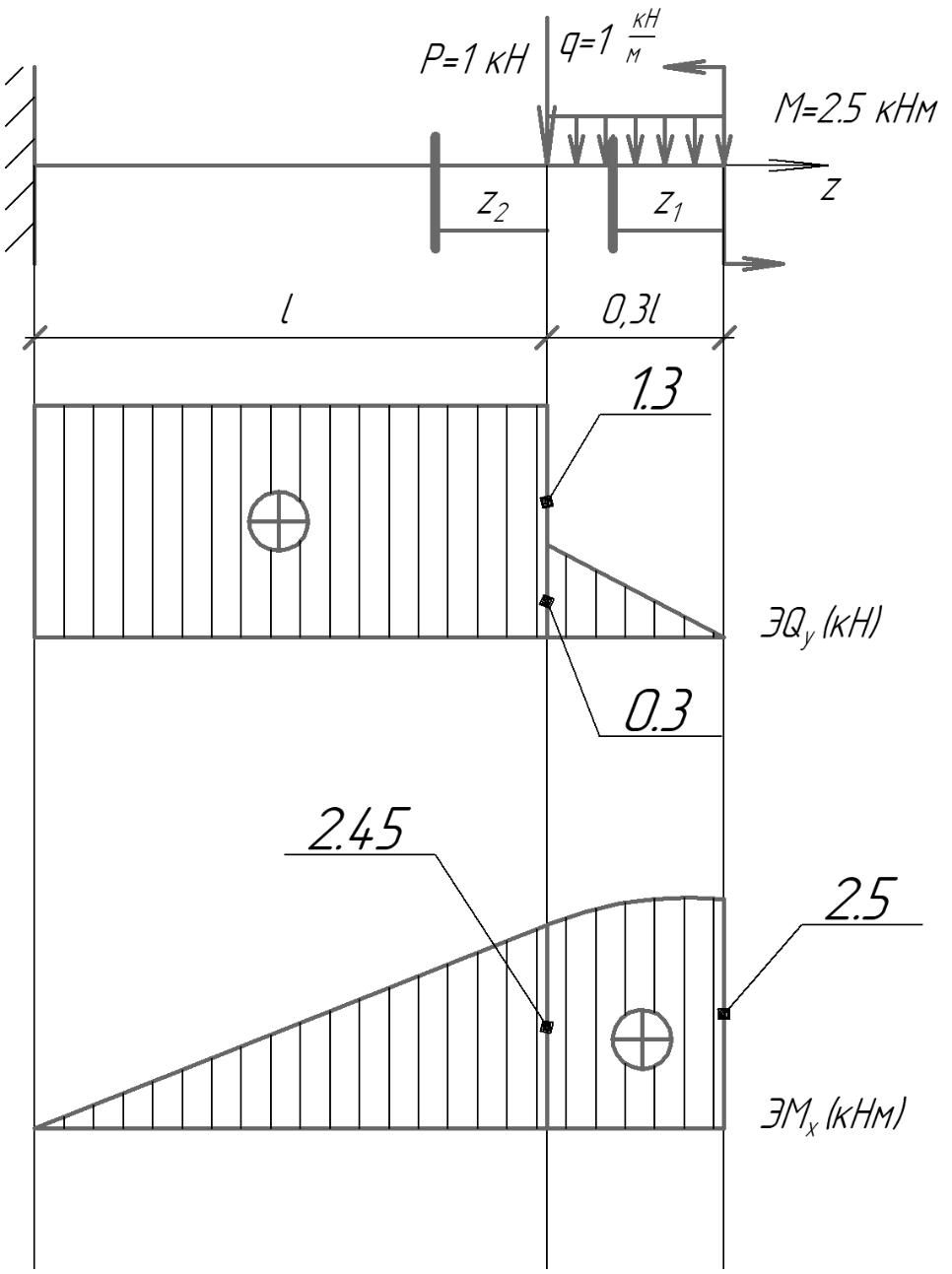  Задача 2   Определяем опорные реакции
Проверка
Намечаем сечения Первый участок:
 Второй участок: Второй участок:
Третий участок:
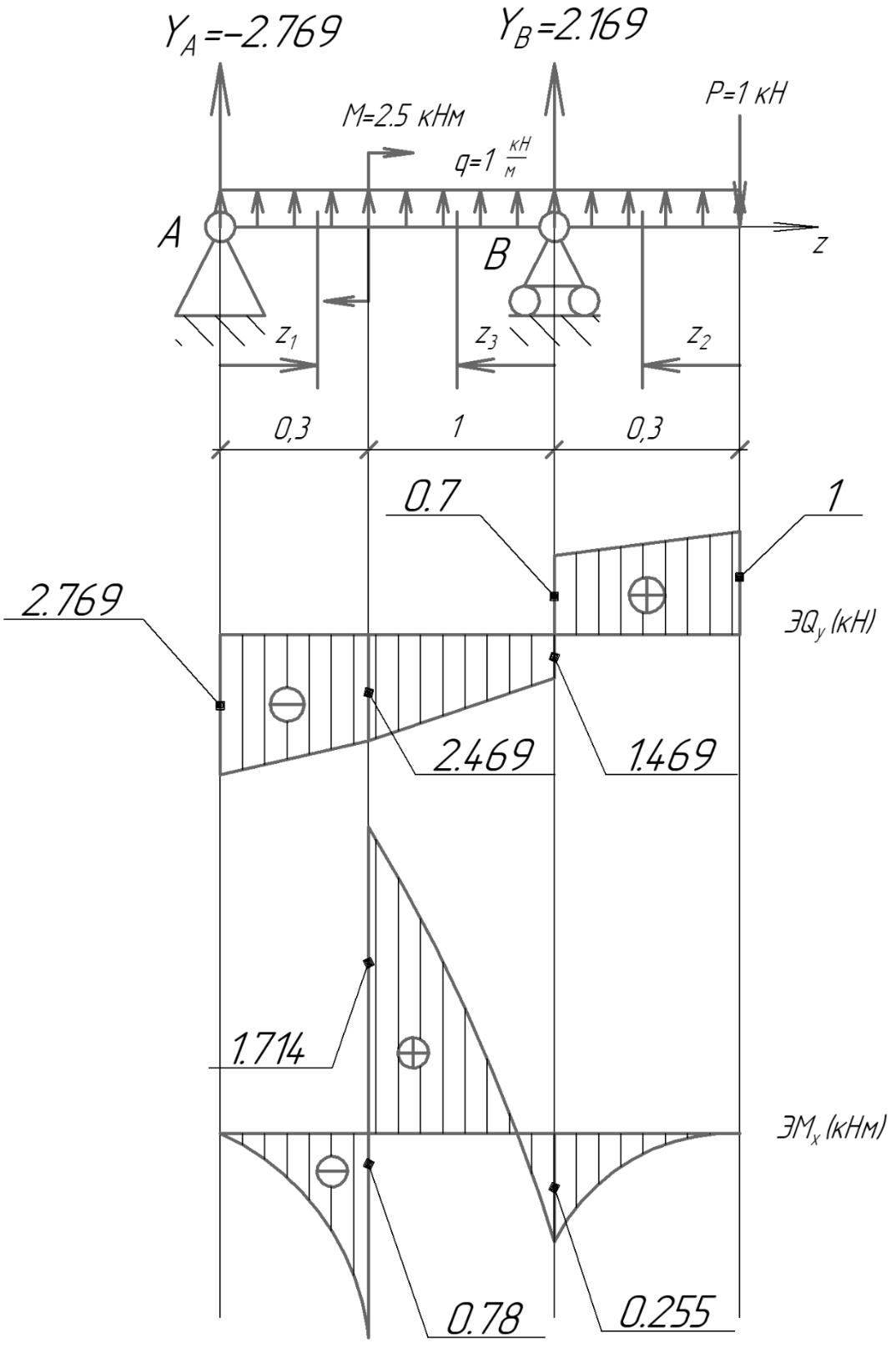  Задача 3  Определяем опорные реакции
Проверка
Намечаем сечения  Первый участок:
 Второй участок: Второй участок:
Третий участок:
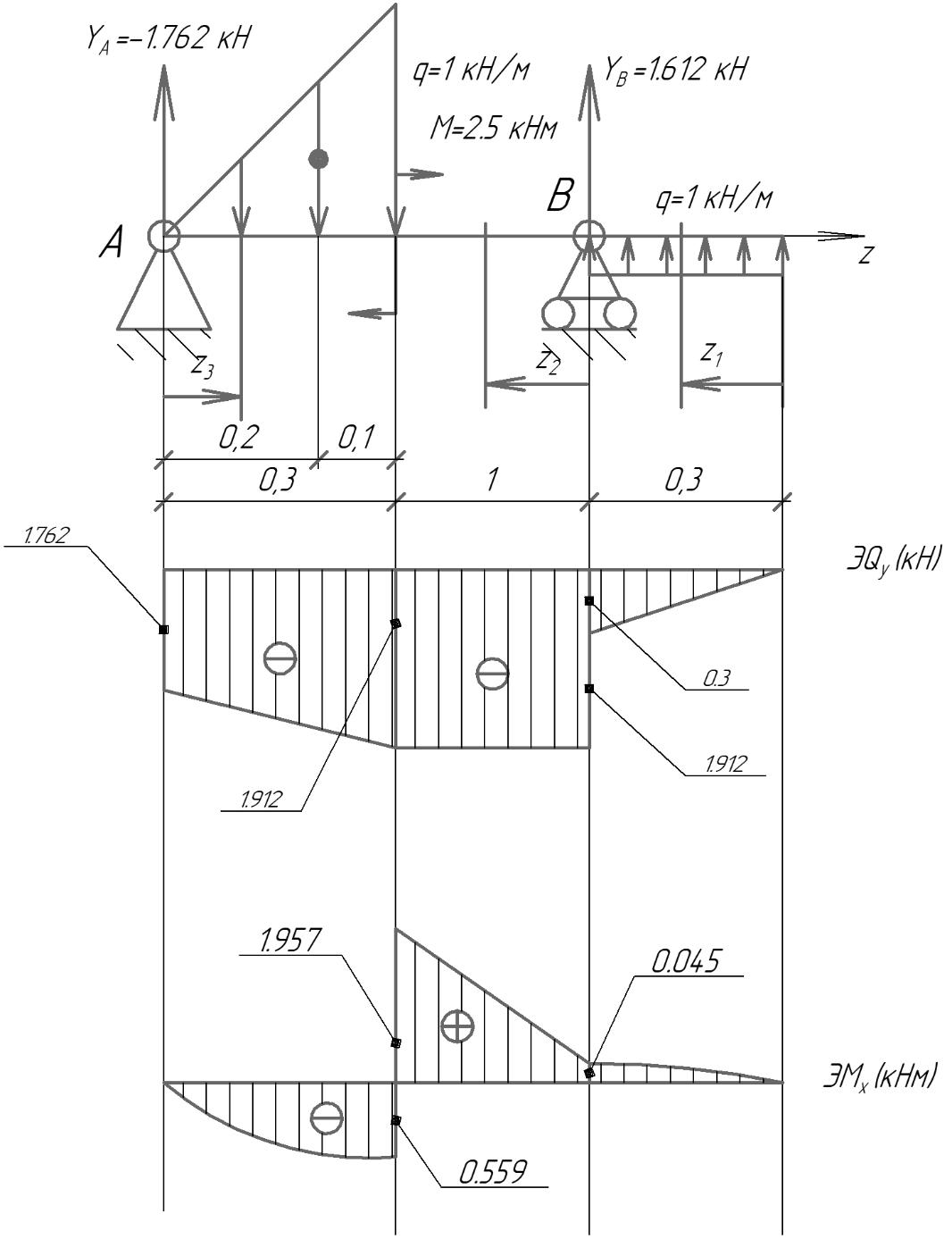  Задача 4  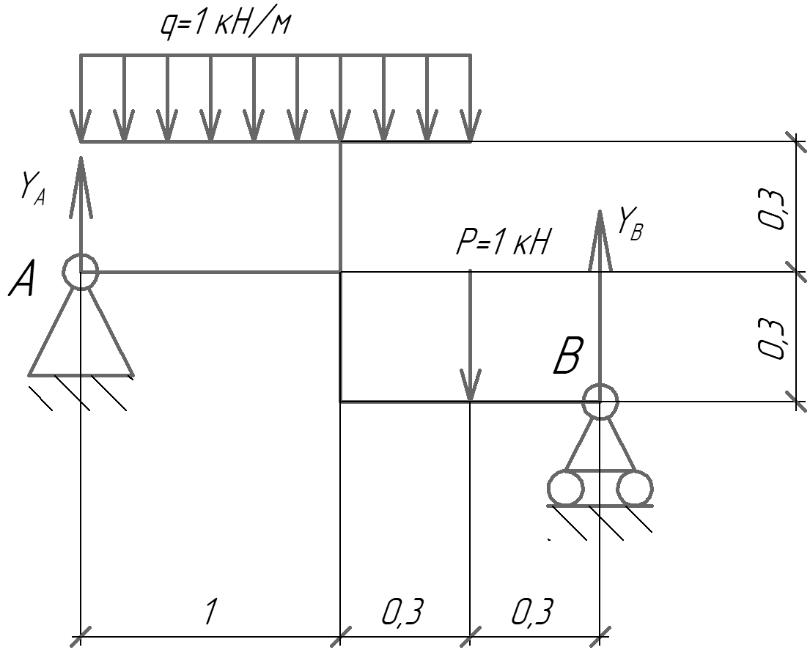 Построение эпюр 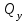 и и 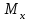 . Опорные реакции. . Опорные реакции. , , 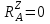 , , 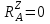 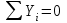 , , 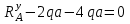 , , 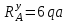 , ,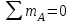 , ,  , , . .Эпюра 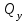 . Она строится по формуле . Она строится по формуле 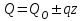 . Поперечная нагрузка постоянна на участках BC и CD ( . Поперечная нагрузка постоянна на участках BC и CD (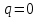 ) и изображается наклонной прямой на участке АВ ( ) и изображается наклонной прямой на участке АВ (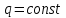 ). Вычисляем значения ). Вычисляем значения 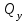 в характерных точках: в характерных точках: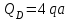 , ,  , , 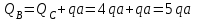 , ,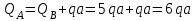 и строим ее эпюру (рисунок 4.1). Эпюра 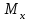 . Она строится по формуле . Она строится по формуле 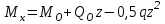 . Изгибающий момент изменяется по квадратичному закону на участке АС ( . Изгибающий момент изменяется по квадратичному закону на участке АС (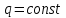 ) и по линейному закону – на всех остальных участках, где ) и по линейному закону – на всех остальных участках, где 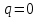 . Вычисляем значения момента на участках бруса: . Вычисляем значения момента на участках бруса: 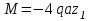 . .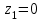 ; ; 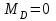 . .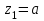 ; ; 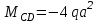 . .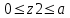 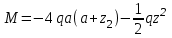 . .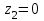 ; ; 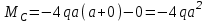 . .  ; ; 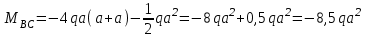 . . 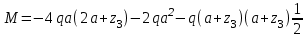 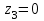 ; ; 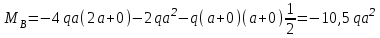 , ,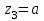 ; ; 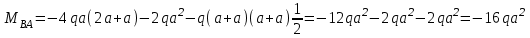 . .строим эпюру 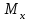 (рисунок 4.1). (рисунок 4.1).Расчетный изгибающий момент равен: 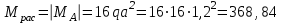 кН·м. кН·м.Подбор сечений. Из условия прочности по нормальным напряжениям 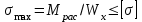 определяем требуемый момент сопротивления поперечного сечения определяем требуемый момент сопротивления поперечного сечения 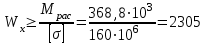 см3, см3,по которому подбираем конкретные сечения. Круг: 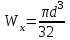 , , 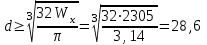 см3. см3.Принимаем по ГОСТ 6636-86 нормализованное значение  мм, тогда мм, тогда 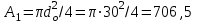 см2. см2.Прямоугольник  : :  , , 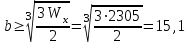 см. см.Ближайшее стандартное значение равно 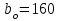 мм. мм.Тогда 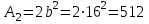 см2. см2.Двутавр. По ГОСТ 8239-89 выбираем двутавр № 60, для которого 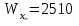 см3, см3,  см2. см2.Два швеллера. По ГОСТ 8240-89 выбираем 2 швеллера № 40, для которых 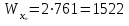 см3. см3. Неравнобокие уголки.Они находятся подбором, так как в ассортименте не даны значения момента сопротивления. Используя формулу Неравнобокие уголки.Они находятся подбором, так как в ассортименте не даны значения момента сопротивления. Используя формулу 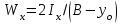 , сделав несколько попыток, последний из сортамента два уголка 250×160×20, для которых , сделав несколько попыток, последний из сортамента два уголка 250×160×20, для которых  см3, см3, 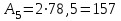 см2. см2.Швеллер и неравнобокие уголки не обеспечивают нужного момент сопротивления поперечного сечения. Оценка экономичности подобранных сечений. Масса балки определяется как произведение плотности материала на ее объем 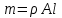 , т.е. расход материала при прочих равных условиям зависит только от площади поперечного сечения A. Сравнивая массы балок , т.е. расход материала при прочих равных условиям зависит только от площади поперечного сечения A. Сравнивая массы балок 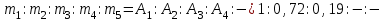 заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, два швеллера, два уголка) достигается экономия, равная соответственно 28%, 81%, -, - , (рисунок 4.2.).  Задача 5 Задача 5 Определяем опорные реакции
Проверка
Намечаем сечения Первый участок:
 Второй участок: Второй участок:
Третий участок:
  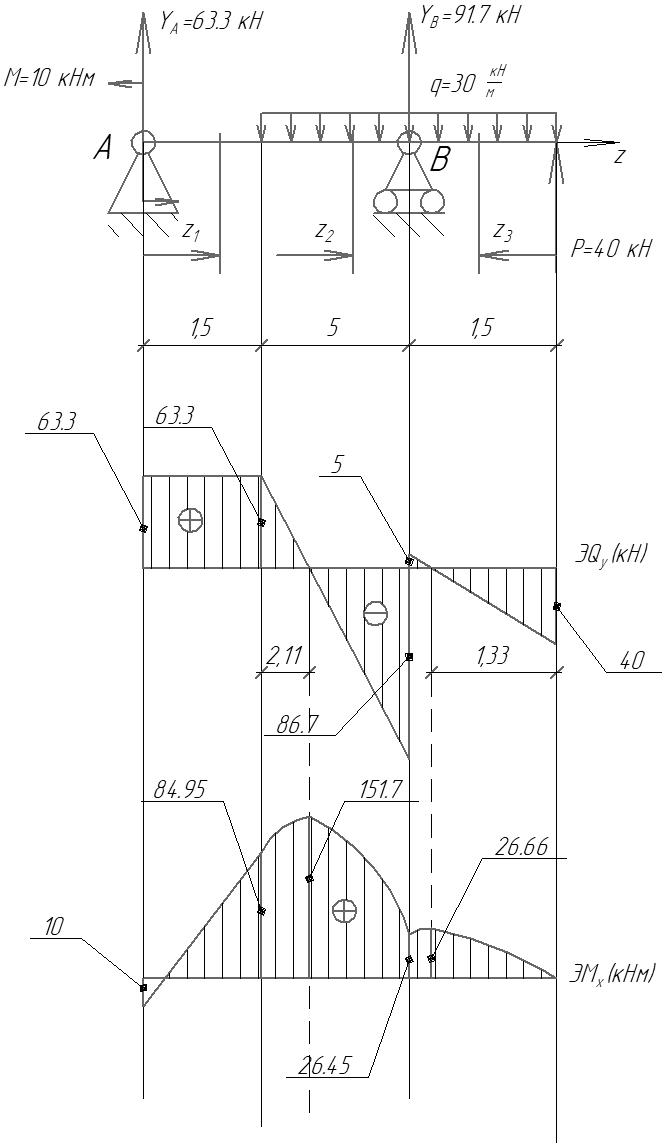 Подбор сечений. Из условия прочности по нормальным напряжениям 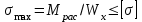 определяем требуемый момент сопротивления поперечного сечения определяем требуемый момент сопротивления поперечного сечения 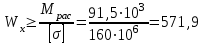 см3, см3,по которому подбираем конкретные сечения. Круг: 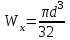 , , 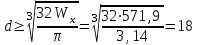 см3. см3.Принимаем по ГОСТ 6636-86 нормализованное значение 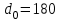 мм, тогда мм, тогда 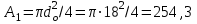 см2. см2.Прямоугольник  : :  , , 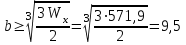 см. см.Ближайшее меньшее стандартное значение равно  мм. При этом балка будет работать с перенапряжением, равным нулю. Тогда мм. При этом балка будет работать с перенапряжением, равным нулю. Тогда 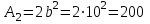 см2. см2.Двутавр. По ГОСТ 8239-89 выбираем двутавра № 33, для которого 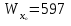 см3, см3, 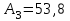 см2. см2.Два швеллера. По ГОСТ 8240-89 выбираем 2 швеллера № 24а, для которых 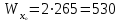 см3, см3, 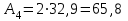 см2. см2.Неравнобокие уголки. Они находятся подбором, так как в ассортименте не даны значения момента сопротивления. Используя формулу 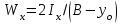 , сделав несколько попыток, выбираем два уголка 250×160×20, для которых , сделав несколько попыток, выбираем два уголка 250×160×20, для которых  см3, см3, 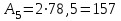 см2. см2. Оценка экономичности подобранных сечений. Масса балки определяется как произведение плотности материала на ее объем Оценка экономичности подобранных сечений. Масса балки определяется как произведение плотности материала на ее объем 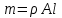 , т.е. расход материала при прочих равных условиям зависит только от площади поперечного сечения A. Сравнивая массы балок , т.е. расход материала при прочих равных условиям зависит только от площади поперечного сечения A. Сравнивая массы балок 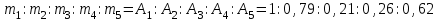 заключаем, что самым неэкономичным является круглое сечение. При замене круга другими формами (прямоугольник, двутавр, два швеллера, два уголка) достигается экономия, равная соответственно 21%, 79%, 74%, 38% (рисунок 7). Исследование напряжений в опорном сечении для балки двутаврого профиля № 33, параметры которой по ГОСТ 8239-89 равны: 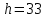 см, см,  см, см, 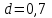 см, см, 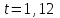 см, см, 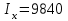 см4, см4, 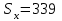 см3. см3.Внутренние силовые факторы в опорном сечении А: 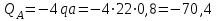 кН; кН; 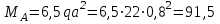 кН·м. кН·м.Эпюра 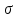 . Нормальное напряжение в поперечном сечении изменяются по линейному закону . Нормальное напряжение в поперечном сечении изменяются по линейному закону 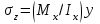 . Вычисляем напряжения в крайних точках . Вычисляем напряжения в крайних точках 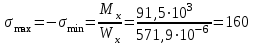 МПа МПаи строим эпюру 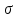 (рисунок 8). (рисунок 8).Эпюра 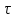 . Она строится по формуле Журавского . Она строится по формуле Журавского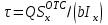 . . Находим значения Находим значения 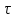 в 4 конкретных точках по высоте сечения (необходимые вычисления представлены в таблице и строим эпюру касательных напряжений. в 4 конкретных точках по высоте сечения (необходимые вычисления представлены в таблице и строим эпюру касательных напряжений.Таблица – Значения 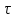 в конкретных точках в конкретных точках
Определение главных напряжений в точке К (  ): ):- напряжения в поперечном сечении 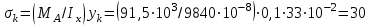 МПа, МПа,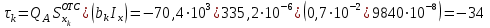 МПа. МПа.- величины главных напряжений  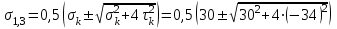 , , 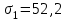 МПа, МПа, 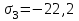 МПа; МПа;- ориентация главных площадок  , откуда , откуда 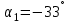 ; ;Экстремальные касательные напряжения равны по величине  МПа МПа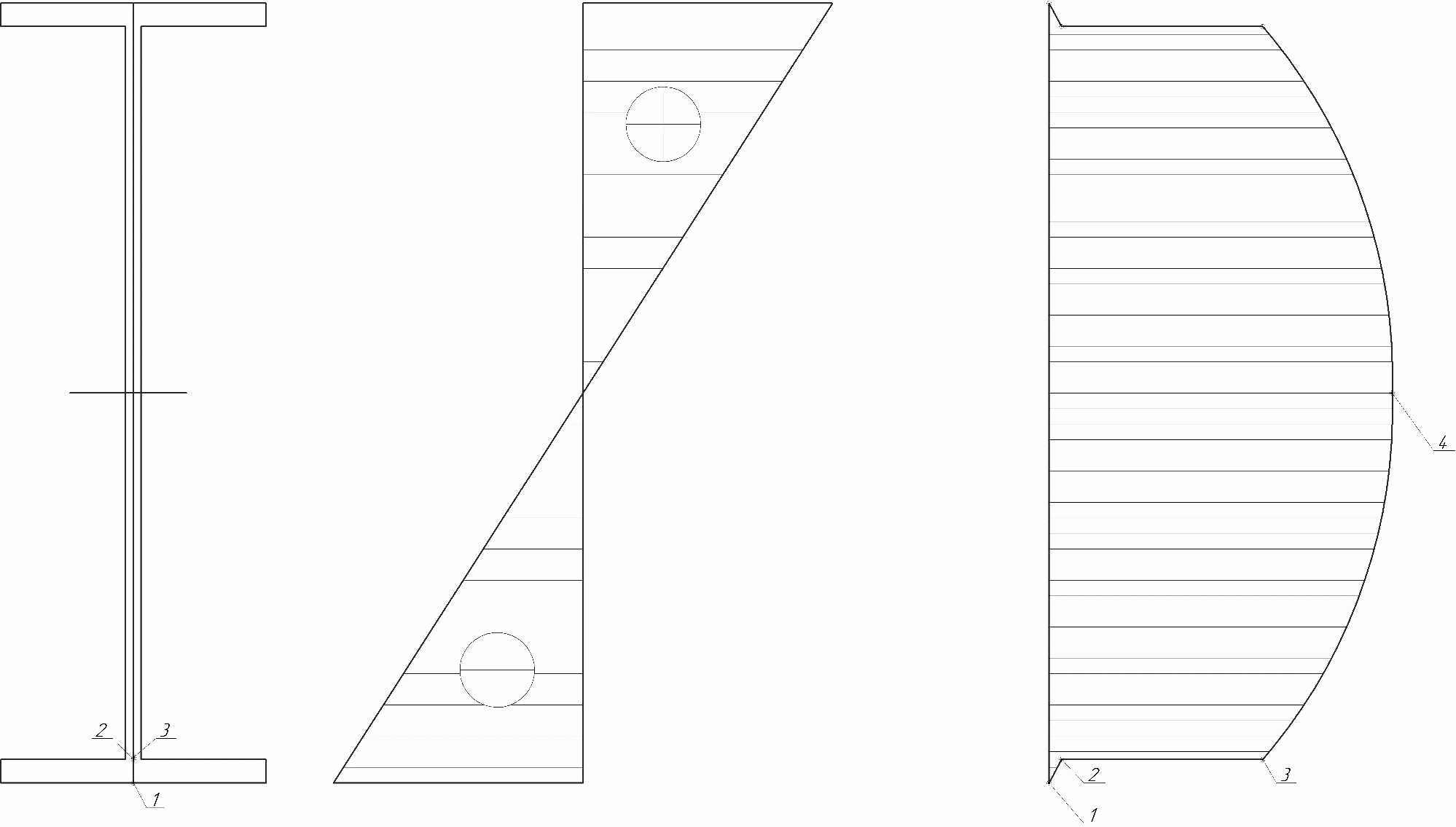 Определение перемещений. Для определения упругих перемещений в инженерной практике применяются как аналитические (точные и приближенные), так и графические методы. Из точных аналитических методов следует отметить метод начальных параметров и энергетический метод. К приближенным относятся метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Ниже определяются линейные и угловые перемещения сечений балки тремя из указанных выше методов. Метод начальных параметров. Из граничных условий задачи имеем 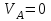 , , 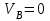 . Найдем . Найдем 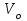 и и  : :  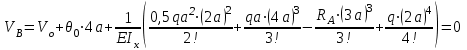 Выражая 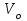 из двух равенств получаем одно, из которого находим из двух равенств получаем одно, из которого находим  . .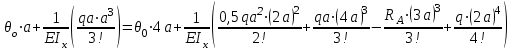 , ,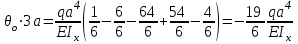 . .Откуда 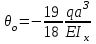 , , 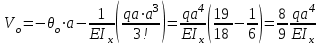 А теперь находим искомые перемещения: - сечение 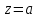 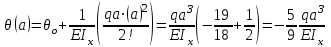 - сечение 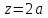 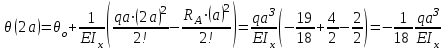 , ,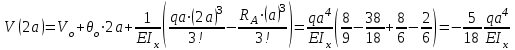 ; ;- сечение 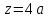 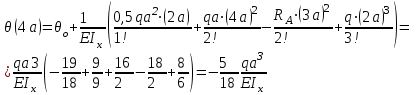 ; ;- сечение 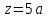 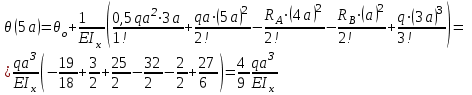 ; ; 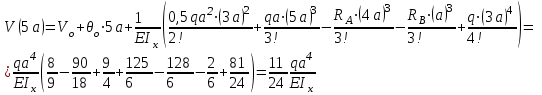 Результаты вычислений сведем в таблицу 8 и построим упругую линию балки, показанную на рисунке 14, а пунктиром. Таблица 8 – Значения углов поворота и перемещений
Для расчета балки на жесткость необходимо знать максимальный прогиб, который имеет место в сечении, где угол поворота равен нулю. Последний описывается полиномом 3-й степени и в связи с этим нахождение максимального прогиба связано с громоздкими вычислениями. С другой стороны, судя по приведенной выше таблице, он имеет место в интервале (а, 3а). В силу непрерывности функции прогибов  мало отличается от прогиба сечения D. Следовательно, с небольшой погрешностью (не превышающей точности инженерных расчетов) можно принять мало отличается от прогиба сечения D. Следовательно, с небольшой погрешностью (не превышающей точности инженерных расчетов) можно принять  . .Энергетический метод. Искомые перемещения находятся с помощью интегралов Мора  , ,для вычисления, которых в простых случаях можно пользоваться правилом Верещагина 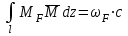 , ,а в более сложных случаях – формулой Симпсона 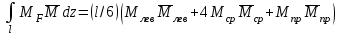 . .При наличии на данном участке равномерно распределенной погонной нагрузки 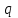 величина момента посередине участка находится следующим образом величина момента посередине участка находится следующим образом . . Величины моментов Величины моментов 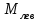 и и  берутся со своими знаками. Знак «плюс» перед вторым слагаемым соответствует погонной нагрузке, направленной вниз, а «минус» - вверх. берутся со своими знаками. Знак «плюс» перед вторым слагаемым соответствует погонной нагрузке, направленной вниз, а «минус» - вверх.Строим эпюры моментов от заданной нагрузки и от единичных воздействий, приложенных к балке в направлении искомых перемещений (рисунок 15). Определяем моменты посередине участков  Перемножая соответствующие эпюры, находим искомые перемещения, увеличенные для удобства вычислений в EIраз: 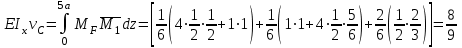 , , 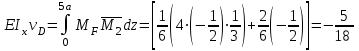 , ,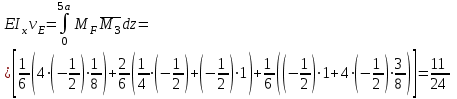 , , , ,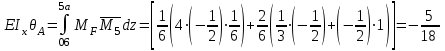 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


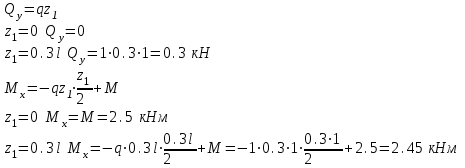
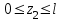
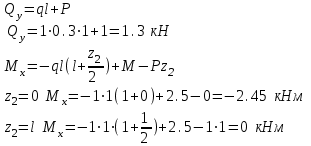
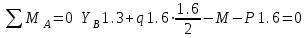

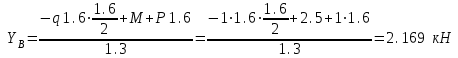
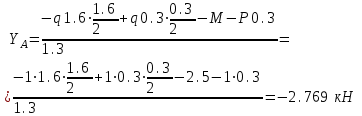
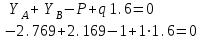
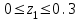
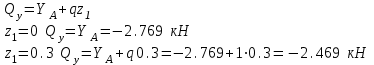
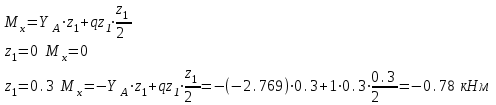

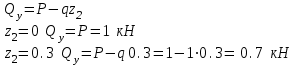
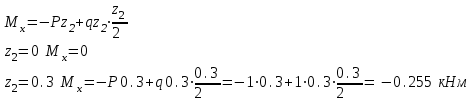


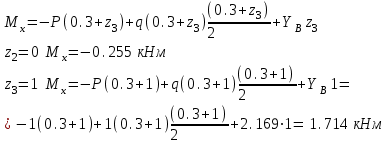

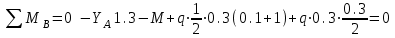
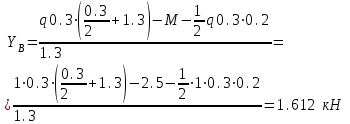
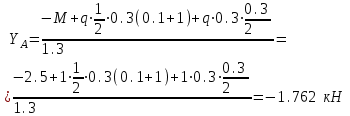
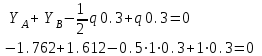
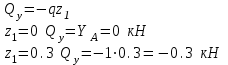
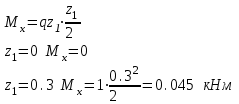
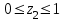
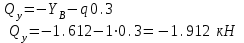

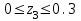
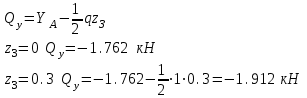
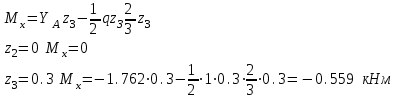
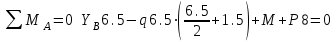
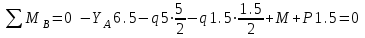
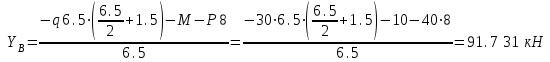
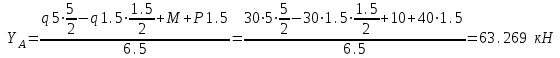
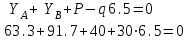
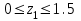
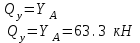
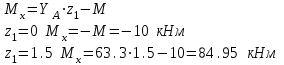
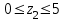
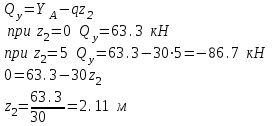
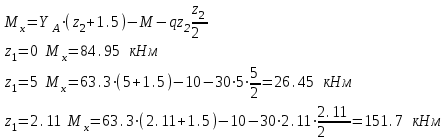
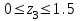
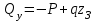

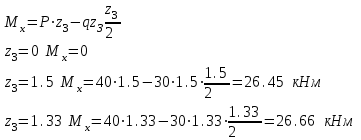
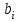 , см
, см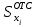 , см3
, см3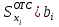
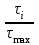
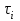 , МПа
, МПа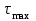
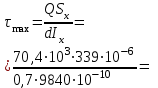
 МПа
МПа