Туманова 3 вариант. 1. Определение основных статистических оценок выборки 3 1 Среднее арифметическое выборки 3
 Скачать 86.14 Kb. Скачать 86.14 Kb.
|
Оглавление1.Определение основных статистических оценок выборки 3 1.1 Среднее арифметическое выборки 3 1.2 Дисперсия 3 1.3 Среднеквадратическое отклонение 4 1.4 Отбраковка по критерию Шовене 4 1.5 Правило «трёх сигм» 4 1.6 Коэффициент вариации V 5 1.7 Доверительный интервал 6 1.8 Необходимое количество экспериментов 6 1.9 Проверка закона распределения СВ 7 1.10 Группировка данных 9 1.Определение основных статистических оценок выборкиИсходные данные Таблица №.1. Вариант 3.
1.1 Среднее арифметическое выборкиСреднее значение – это среднеарифметическое из всех измеренных значений: 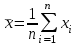 , (1.1.1) , (1.1.1)где 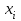 - значение случайной величины, n – количество случайной величины; - значение случайной величины, n – количество случайной величины;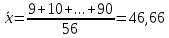 1.2 ДисперсияМерой отклонения случайной величины от средних значений служит дисперсия и среднеквадратическое отклонение. Дисперсия – это число, равное среднему квадрату отклонений значений случайной величины от её среднего значения: 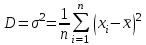 , (1.2.1) , (1.2.1)где D – дисперсия. D = 123,94 1.3 Среднеквадратическое отклонениеСреднеквадратическое отклонение – это число, равное квадратному корню из дисперсии: 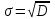 (1.3.1) (1.3.1)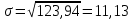 1.4 Отбраковка по критерию ШовенеПри проведении опытов при одинаковых условиях часто наблюдаются значения, резко отличающиеся от остальных. Отбраковка таких значений производится с помощью специальных методов. В работе мы использовали критерий Шовене. 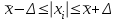 , (1.4.1) , (1.4.1)где 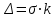 , k – коэффициент Шовене, для n =56 он равен 2,61. , k – коэффициент Шовене, для n =56 он равен 2,61.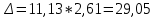 46,66-29,05 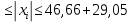 17,61 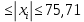 В интервал не вошли элементы выборки 9; 10: 12; 90. Так как эти значения резко отличаются от остальных, то мы их отбраковываем. 1.5 Правило «трёх сигм»Правило «трёх сигм» основано на том, что случайная величина при нормальном законе распределения практически полностью (на 99,7%) заключена в пределах от 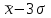 до до 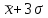 . Если значение случайной величины отличается от среднего значения . Если значение случайной величины отличается от среднего значения 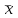 больше чем на 3 больше чем на 3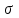 , то оно является аномальным. , то оно является аномальным.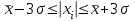 (1.5.1) (1.5.1)46,66 –3*11,13 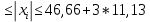 13,27 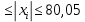 В интервал не вошли элементы выборки 9; 10: 12; 90. Так как эти значения отличается от среднего значения 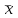 больше чем на 3 больше чем на 3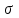 , то мы их считаем аномальными. , то мы их считаем аномальными.1.6 Коэффициент вариации VНа практике широко применяют также характеристику рассеяния, называемую коэффициентом вариации V, который представляет собой отношение среднего квадратичного отклонения к среднему значению. Коэффициент вариации показывает насколько велико рассеяние по сравнению со средним значением случайной величины. Коэффициент вариации выражается в долях единицы или в процентах. Вычисление коэффициента вариации имеет смысл для положительных случайных величин: 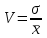 (1.6.1) (1.6.1)V = 11,13/46,66 = 0,24 = 24% 1.7 Доверительный интервалИнтервальная оценка с принятой вероятностью p или уровнем значимости 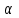 определяет диапазон, в котором с определённой вероятностью будет находится истинное значение средней величины определяет диапазон, в котором с определённой вероятностью будет находится истинное значение средней величины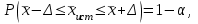 (1.7.1) (1.7.1)где Р – это доверительная вероятность, α – уровень значимости 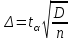 , (1.7.2) , (1.7.2)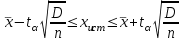 (1.7.3) (1.7.3)k = n–1, (1.7.4) где k – степень свободы, 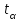 - критерий Стьюдента, для 56 равен 2,09 с α=0,05. - критерий Стьюдента, для 56 равен 2,09 с α=0,05.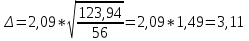 46,66 –3,11 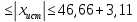 43,55 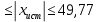 В диапазоне от 35 до 58 будет находиться истинное значение средней величины с вероятностью 0,95 1.8 Необходимое количество экспериментовЗависит от точности, которую нам нужно получить. 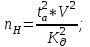 (1.8.1) (1.8.1)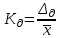 (1.8.2) (1.8.2)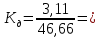 0,07 0,07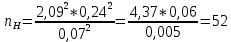 1.9 Проверка закона распределения СВНормальный закон распределения выполняется в том случае, если соблюдается два условия: 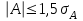 (1.9.1) (1.9.1)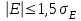 (1.9.2) (1.9.2)где A – показатель асимметрии (характеризует симметричность левой и правой ветвей кривой), равный 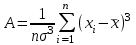 . (1.9.3) . (1.9.3)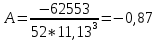 А= -0,87 Е - показатель эксцесса (характеризует форму вершины кривой), 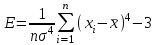 , (1.9.4) , (1.9.4)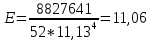 Е = 11,06 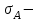 среднеквадратическое отклонение асимметрии нормального закона. среднеквадратическое отклонение асимметрии нормального закона.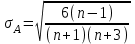 , (1.9.5) , (1.9.5)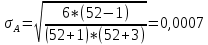 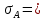 0,0007 0,0007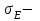 среднеквадратическое отклонение эксцесса нормального распределения среднеквадратическое отклонение эксцесса нормального распределения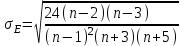 , (1.9.6) , (1.9.6)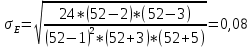 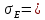 0,08 0,080,81≤1,5*0,0007 0,81>0,00105 10,26≤1,5*0,08 10,26>0,12 Оба условия не выполнены, следовательно, выборка не подчиняется нормальному закону распределения. 1.10 Группировка данныхВесь диапазон данных разбивают на классы. 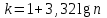 (1.10.1) (1.10.1)где 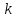 - количество классов. - количество классов. k = 1+3,32*lg56 = 1+3,32*1,75 = 6,81 Результат округляем до целого. Размер каждого класса находим по формуле: 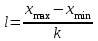 (1.10.2) (1.10.2)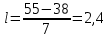 Таблица №2
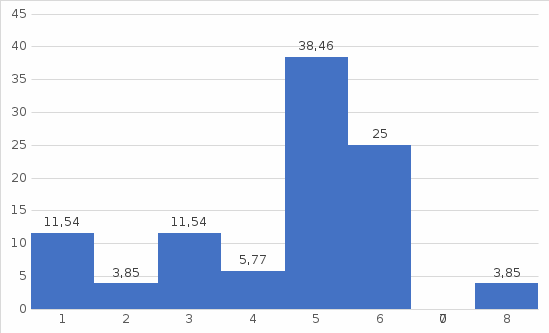 Рис. 1.10. Гистограмма. Распределение случайной величины хорошо отражается приведённой гистограммой. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
