|
|
Реферат. Реферат Османов Ислам. Рассеяние света и явление Тиндаля
Федеральное государственное учреждение высшего образования
«Астраханский государственный медицинский университет»
Министерства здравоохранения Российской Федерации
Реферат на тему:
«Рассеяние света и явление Тиндаля»
Выполнил:
Студент 1 курса 108 группы
Стоматологического факультета
Османов Ислам
Астрахань 2022
План реферата:
Распространение света в оптически неоднородной среде; явление Тиндаля
Природа процессов рассеяния света
Рэлеевское рассеяние и рассеяние Ми
Физическая сущность комбинационного рассеяния и рассеяния Мандельштама – Бриллюэна
Список Литературы
Когерентное рассеяние света
Вторичные волны, обусловленные колебаниями электронов среды, уносят часть энергии, приносимой световой волной. Иначе говоря, распространение света в веществе должно сопровождаться рассеянием света. Казалось бы, наличие электронов, колеблющихся под действием электромагнитной волны, достаточно для возникновения рассеянных волн. Однако несложно показать, что однородность среды и когерентность вторичных волн – условия, необходимые и достаточные для того, чтобы рассеянный свет не мог возникнуть.
Так как в действительности идеально однородных сред не существует, то есть реальные среды оптически неоднородны, то они в той или иной мере рассеивают свет.
Неоднородность среды может быть обусловлена флуктуациями концентрации частиц, присутствием посторонних частиц, на которых свет испытывает дифракцию (рассеивается).
Однако среда может быть оптически однородной, будучи физически неоднородной (стеклянная палочка в кедровом масле), если показатели преломления обоих веществ одинаковы. Однако такая сложная среда оказывается оптически однородной в узком спектральном интервале. При достаточной толщине кюветы взвесь стеклянных частиц в жидкости может служить хорошим светофильтром, пропуская свет в узком спектральном диапазоне и рассеивая волны, длина которых не входит в этот интервал. При незначительном нагревании такой кюветы можно наблюдать, как меняется окраска проходящего света, что обусловлено различной зависимостью от температуры показателя преломления стекла и жидкости. Эта особенность используется в мелкодисперсных фильтрах, предназначенных для работы в ИК области спектра (Б.И. Борисевич, Верещагин и др.; государственная премия).
Рассеяние света на частицах, малых по сравнению с длиной волны видимого света, в лабораторных условиях впервые наблюдал Тиндаль (1869 г.). Он обратил внимание на то, что рассеянный под различными углами свет отличается от падающего белого света наличием синего оттенка, а свет, рассеянный под углом 90º относительно направления падающего света, полностью или почти полностью линейно поляризован.
Во многих ситуациях наблюдается интенсивное рассеяние света вследствие естественно возникшей оптической неоднородности. Среды с явно выраженной оптической неоднородностью называют мутными средами (дым, туман, взвеси или суспензии и т.п.). Во всех этих случаях наблюдается более или менее сильное рассеяние света мутной средой, называемое обычно явлением Тиндаля. Теоретическое описание этого явления было дано Рэлеем.
B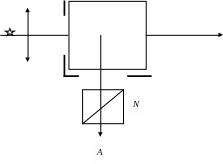
Распределение интенсивностей света, рассеянного под разными углами, симметрично относительно оси первичного пучка и относительно линии, ей перпендикулярной.
К ривая, графически представляющая распределение интенсивности рассеянного света по разным направлениям, называется индикатрисой рассеяния. Если падающий свет естественный, то индикатриса рассеяния света на частицах, малых по сравнению с длиной волны, описывается формулой Рэлея: ривая, графически представляющая распределение интенсивности рассеянного света по разным направлениям, называется индикатрисой рассеяния. Если падающий свет естественный, то индикатриса рассеяния света на частицах, малых по сравнению с длиной волны, описывается формулой Рэлея:
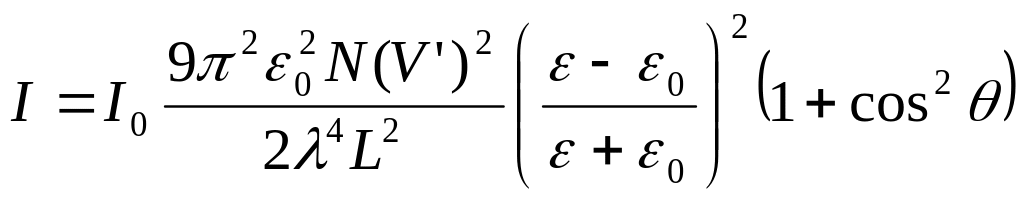 . .
Здесь N – число частиц в рассеивающем объеме, V’ и  – объем и диэлектрическая проницаемость частицы, – объем и диэлектрическая проницаемость частицы,  – диэлектрическая проницаемость среды, в которой взвешены частицы, – диэлектрическая проницаемость среды, в которой взвешены частицы,  – угол рассеяния, – угол рассеяния,  – интенсивность падающего света, – интенсивность падающего света,  – интенсивность рассеянного света, L – расстояние от рассеивающего объема до точки наблюдения. – интенсивность рассеянного света, L – расстояние от рассеивающего объема до точки наблюдения.
Таким образом, интенсивность рассеянного света обратно пропорциональна четвертой степени длины волны. Этот закон ( ) называют законом Рэлея. ) называют законом Рэлея.
Из формулы Рэлея видно, что интенсивность рассеянного света пропорциональна квадрату объема (шестой степени радиуса) рассеивающих частиц.
Множитель  может служить мерой оптической неоднородности среды. При может служить мерой оптической неоднородности среды. При  рассеянный свет отсутствует. рассеянный свет отсутствует.
Отмеченные выше закономерности рассеяния света не выполняются, если размеры рассеивающих частиц сравнимы с длиной волны, что часто имеет место в коллоидных растворах. При этом рассеянный свет поляризован частично, степень поляризации зависит от размеров частиц, зависимость интенсивности рассеянного света от длины волны менее заметна, и индикатриса рассеяния несимметрична относительно линии АА и может иметь сложный вид.
Рассеяние света мелкими частицами обусловливает ряд явлений, которые можно описать на основе теории дифракции света на диэлектрических частицах. Многие характерные особенности рассеяния света частицами удаётся проследить в рамках смтрогой теории, разработанной для сферических частиц английским ученым А. Лявом (1889) и немецким ученым Г. Ми (1908, теория Ми). Когда радиус частицы r значительно меньше длины волны λn света в веществе, рассеяние света на ней аналогично нерезонансному рассеянию света атомом. Сечение и интенсивность рассеяния света в таких условиях сильно зависит от r и от разности диэлектрических проницаемостей частицы ε и окружающей среды ε0:  (английский физик Рэлей, 1871). С увеличением r до r (английский физик Рэлей, 1871). С увеличением r до r λn и более (при условии ε > 1) в индикатрисе рассеяния появляются резкие максимумы и минимумы. Вблизи так называемых резонансов Ми, которые реализуются при выполнении условия  (где m = 1, 2, 3, …), сечения сильно возрастают и становятся равными (где m = 1, 2, 3, …), сечения сильно возрастают и становятся равными  ; рассеяние вперёд усиливается, назад – ослабевает; зависимость поляризации света от угла рассеяния сильно усложняется. ; рассеяние вперёд усиливается, назад – ослабевает; зависимость поляризации света от угла рассеяния сильно усложняется.
Тиндаль высказал предположение, что голубой цвет неба, объясняется рассеянием солнечного света на пылинках, взвешенных в атмосфере Земли. Однако при исследовании рассеяния света в высокогорных районах было установлено, что голубой цвет неба обусловлен молекулярным рассеянием, а не рассеянием на малых частицах. Молекулярное рассеяние света реализуется также на флуктуациях плотности вещества, находящегося в критическом состоянии, на флуктуациях концентрации в некоторых растворах, на молекулярных шероховатостях поверхности жидкости и границы двух жидкостей, особенно вблизи критической температуры смешения. Флуктуации плотности вещества, обусловленные статистическим характером теплового движения молекул, имеют место и в чистых веществах, не содержащих примесей. Эти флуктуации являются причиной флуктуаций показателя преломления ( ) и диэлектрической проницаемости ( ) и диэлектрической проницаемости ( ), нарушающих однородность среды. В электродинамике получена формула, которой определяется интенсивность света, рассеянного на флуктуациях диэлектрической проницаемости: ), нарушающих однородность среды. В электродинамике получена формула, которой определяется интенсивность света, рассеянного на флуктуациях диэлектрической проницаемости:
 . .
Здесь V* – объем флуктуации, малый по сравнению с длиной световой волны, но содержащий много молекул. В случае молекулярного рассеяния мерой оптической неоднородности является величина 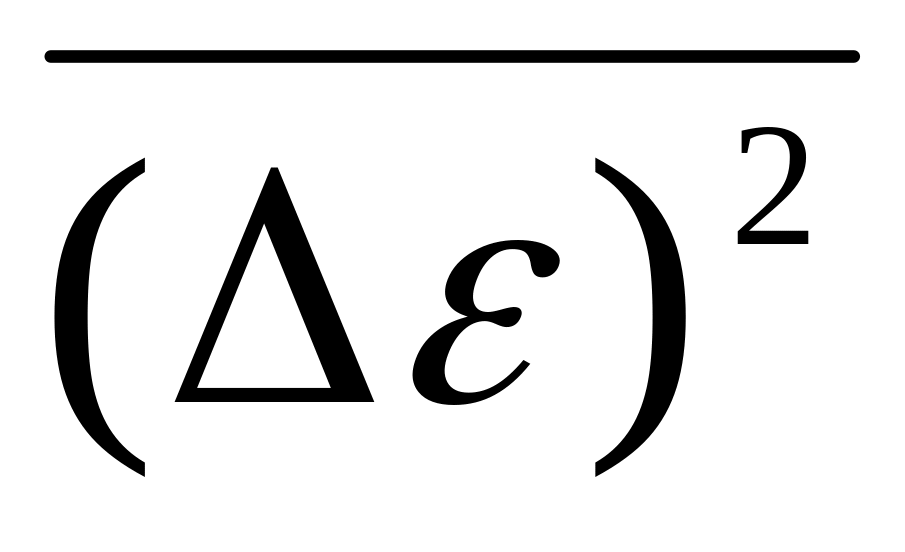 . .
Эйнштейном была получена формула, носящая его имя,
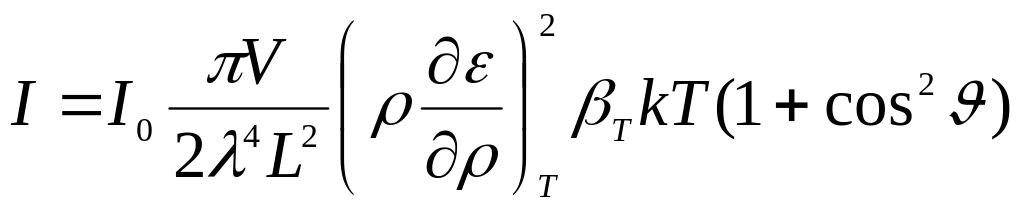 , ,
в которой учтена зависимость интенсивности рассеянного света от изотермической сжимаемости среды  . .
Во всех записанных здесь выражениях интенсивность рассеянного света  , то есть справедлив закон Рэлея. Именно молекулярным рассеянием объясняется голубой цвет неба и красный цвет Солнца на закате. Исследования интенсивности молекулярного рассеяния стали основой для экспериментального определения числа Авогадро. , то есть справедлив закон Рэлея. Именно молекулярным рассеянием объясняется голубой цвет неба и красный цвет Солнца на закате. Исследования интенсивности молекулярного рассеяния стали основой для экспериментального определения числа Авогадро.
1908 г. Польским физиком М. Смолуховским было исследовано рассеяние света на флуктуациях плотности вещества, находящегося в критическом состоянии. Этот вид рассеяния света называют критической опалесценцией. Интенсивность рассеяния при критической опалесценции велика.
Теоретически показано, что свет, рассеянный на флуктуациях плотности, полностью линейно поляризован в плоскости, перпендикулярной к плоскости рассеяния. Свет, рассеянный на флуктуациях анизотропии, деполяризован, при этом степень деполяризации равна 6/7 при освещении рассеивающей среды естественным светом и 3/4 – при освещении линейно поляризованным светом с электрическим вектором, перпендикулярным к плоскости рассеяния при наблюдении рассеяния под углом 900. При одновременном влиянии обеих причин рассеянный свет частично поляризован (даже при наблюдении в направлении, перпендикулярном направлению падающего пучка в котором свет, рассеянный молекулой должен быть полностью поляризован). Если падающий пучок распространяется в направлении оси OY, то степень деполяризации рассеянного света 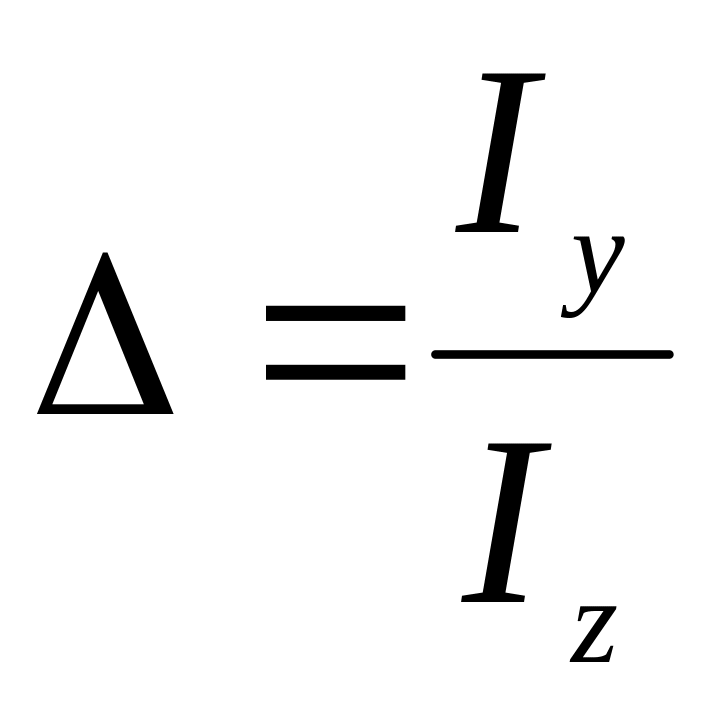 варьирует в широких пределах. Так, для водорода она равна 1 %, для азота – 4 %, для паров сероуглерода – 14 %, для углекислоты – 7 %. Для жидкостей степень деполяризации еще больше: для бензола 44 %, для сероуглерода 68 %, для нитротолуола 80 %. Частичная деполяризация света при рассеянии объясняется анизотропией молекул, то есть теми же свойствами среды, что и эффект Керра. Поляризационные измерения рассеянного изучения используются в целях изучения структуры молекул. варьирует в широких пределах. Так, для водорода она равна 1 %, для азота – 4 %, для паров сероуглерода – 14 %, для углекислоты – 7 %. Для жидкостей степень деполяризации еще больше: для бензола 44 %, для сероуглерода 68 %, для нитротолуола 80 %. Частичная деполяризация света при рассеянии объясняется анизотропией молекул, то есть теми же свойствами среды, что и эффект Керра. Поляризационные измерения рассеянного изучения используются в целях изучения структуры молекул.
Всем рассмотренным нами до сих пор видам рассеяния света свойственно то, что частота излучения при рассеянии не изменяется, то есть рассеяние когерентно.
Комбинационное рассеяние света
При тщательном изучении спектров рассеянного света Раманом, Г.С. Ландсбергом и Л.И. Мандельштамом в 1928 г. было показано, что в спектре рассеянного света, кроме линий, характеризующих падающий свет, присутствуют добавочные линии-спутники, сопровождающие каждую линию первичного спектра. Так как линии-спутники сопровождают каждую линию первичного спектра, то ясно, что обнаружение их возможно только в том случае, если падающий свет представляет собой совокупность отдельных монохроматических линий, а не сплошной.
Для наблюдения спектров комбинационного рассеяния света необходимо сконцентрировать интенсивный пучок света на изучаемом объекте О. В качестве источника возбуждающего излучения применяют ртутную лампу, в последние десятилетия чаще используют лазеры. Рассеянный свет фокусируется и регистрируется фотографическим (спектрограф) или фотоэлектрическим (спектрофотометр) методом. Экран Э используется для устранения возбуждающего излучения. Конденсоры К1и К2 используются соответственно для концентрации излучения на исследуемом объекте и для фокусирования рассеянного излучения на входной щели спектрального прибора.
Опытным путем установлены следующие законы этого явления:
спутники сопровождают каждую линию первичного света;

различие  в частотах возбуждающего первичного излучения в частотах возбуждающего первичного излучения 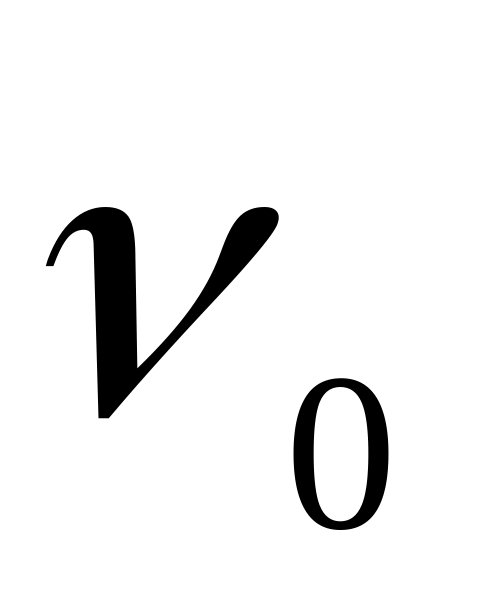 и линий-спутников и линий-спутников  , , 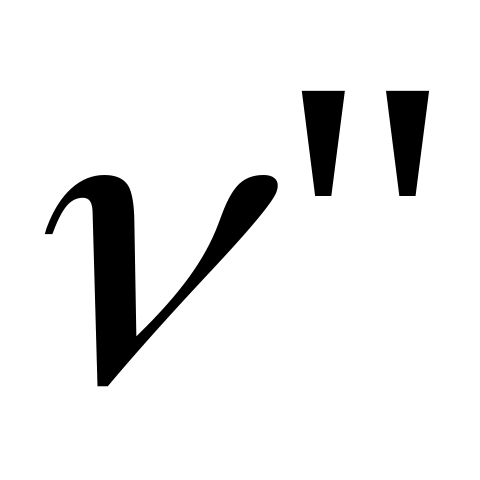 , , 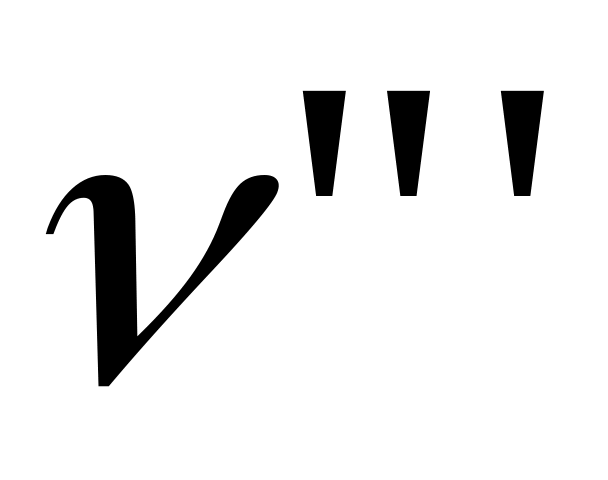 , … характерно для рассеивающего вещества и равно частотам колебаний , … характерно для рассеивающего вещества и равно частотам колебаний 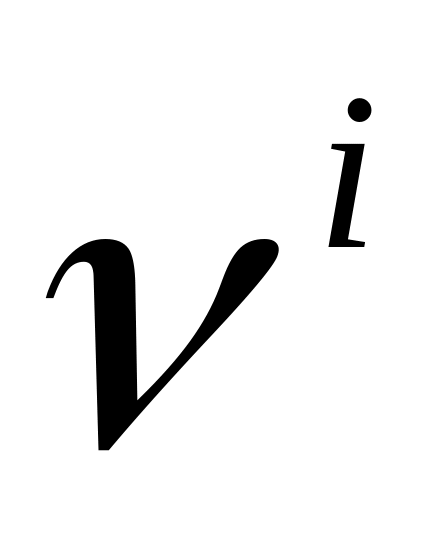 его молекул: его молекул:
 , ,  , ,  , …; , …;
спутники представляют собой две системы линий, расположенных симметрично относительно возбуждающей линии, то есть
 , ,
где  и и  – соответственно частоты коротковолнового («фиолетового», или антистоксова) и длинноволнового («красного», или стоксова) спутников возбуждающей линии. Интенсивность красных спутников обычно значительно больше интенсивности фиолетовых спутников; – соответственно частоты коротковолнового («фиолетового», или антистоксова) и длинноволнового («красного», или стоксова) спутников возбуждающей линии. Интенсивность красных спутников обычно значительно больше интенсивности фиолетовых спутников;
с повышением температуры интенсивность «фиолетовых» спутников быстро возрастает.
Комбинационное рассеяние наиболее часто связано с переходами между колебательными уровнями энергии молекул, и, измеряя частоты линий комбинационного рассеяния, можно определить частоты собственных (или нормальных) колебаний молекулы. Аналогичные закономерности наблюдаются и для вращательных спектров комбинационного рассеяния света.
В квантовой теории механизм комбинационного рассеяния света разделяют на два этапа:
1) поглощение первичного фотона с энергией  и и
2) испускание фотона с энергией  (где (где 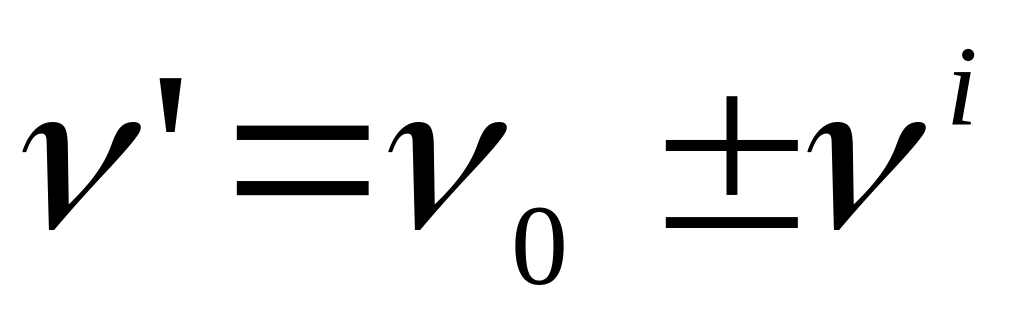 ), происходящее в результате взаимодействия электронов молекулы с полем падающей электромагнитной волны. ), происходящее в результате взаимодействия электронов молекулы с полем падающей электромагнитной волны.
Молекула, находящаяся в невозбужденном состоянии, под действием кванта с энергией сначала переходит в промежуточное электронное состояние, а затем – в состояние с колебательной энергией  , испуская при этом квант , испуская при этом квант  . Этот процесс сопровождается появлением в рассеянном свете стоксовой линии с частотой . Этот процесс сопровождается появлением в рассеянном свете стоксовой линии с частотой  . .
Если фотон поглощается системой, в которой уже возбуждены колебания, то после рассеяния она может перейти в невозбужденное (нулевое) состояние, при этом энергия рассеянного фотона превышает энергию поглощенного кванта. Этот процесс приводит к появлению антистоксова спутника.
Вероятность  комбинационного рассеяния, а следовательно, интенсивность линий КРС зависит от интенсивностей возбуждающего I0 и рассеянного I излучения: комбинационного рассеяния, а следовательно, интенсивность линий КРС зависит от интенсивностей возбуждающего I0 и рассеянного I излучения:
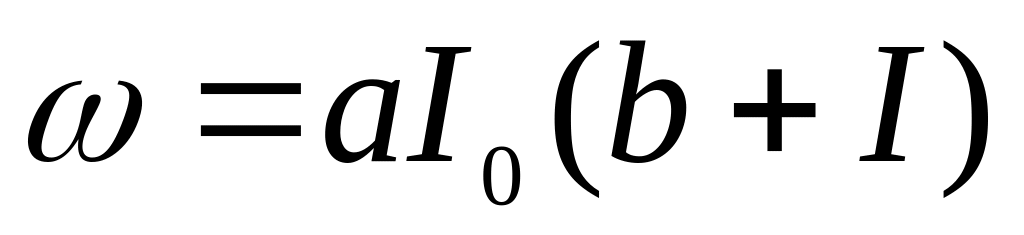 , ,
где a и b – постоянные величины. При возбуждении КРС обычными источниками второе слагаемое,  мало, и им можно пренебречь. Интенсивность линий КРС в большинстве случаев весьма мала; при этом при обычных температурах интенсивность антистоксовых линий значительно меньше интенсивности стоксовых линий, отношение интенсивностей мало, и им можно пренебречь. Интенсивность линий КРС в большинстве случаев весьма мала; при этом при обычных температурах интенсивность антистоксовых линий значительно меньше интенсивности стоксовых линий, отношение интенсивностей  определяется отношением населенностей возбужденного и основного уровней. С повышением температуры населенность возбужденного уровня возрастает, и растет интенсивность антистоксовых линий. определяется отношением населенностей возбужденного и основного уровней. С повышением температуры населенность возбужденного уровня возрастает, и растет интенсивность антистоксовых линий.
Интенсивность КРС зависит от частоты возбуждающего света. На больших расстояниях (в шкале частот) от области электронного поглощения она пропорциональна  , при приближении к частоте электронного поглощения наблюдается более быстрый рост интенсивности линий КРС. В некоторых случаях при малых концентрациях вещества удается наблюдать резонансное КРС, когда частота возбуждающего света попадает в область поглощения света. При возбуждении КРС лазерами вероятность КРС возрастает и возникает вынужденное КРС, интенсивность которого того же порядка, что и интенсивность возбуждающего света. , при приближении к частоте электронного поглощения наблюдается более быстрый рост интенсивности линий КРС. В некоторых случаях при малых концентрациях вещества удается наблюдать резонансное КРС, когда частота возбуждающего света попадает в область поглощения света. При возбуждении КРС лазерами вероятность КРС возрастает и возникает вынужденное КРС, интенсивность которого того же порядка, что и интенсивность возбуждающего света.
Рассеяние Мандельштама – Бриллюэна
Рассеяние Мандельштама – Бриллюэна – это рассеяние оптического излучения конденсированными средами (твёрдыми телами и жидкостями) в результате его взаимодействия с собственными упругими колебаниями этих сред. Рассеяние Мандельштама – Бриллюэна сопровождается изменением частот (длин волн), характеризующих излучение. Например, рассеяние Мандельштама – Бриллюэна монохроматического света внутри кристалла обусловливает появление шести компонентов рассеянного света, в жидкостях – трёх (один из них неизменённой частоты).
Сравнительно сильное взаимодействие между частицами конденсированных сред (в кристаллах оно связывает их в упорядоченную пространственную решётку) обусловливает то, что по всевозможным направлениям в среде распространяются упругие волны различных частот (гиперзвук). В результате наложения таких волн друг на друга возникают флуктуации плотности среды, на которых и рассеивается свет. При исследовании рассеяния Мандельштама – Бриллюэна показано, что световые волны взаимодействуют не только с флуктуациями плотности, но и непосредственно с упругими волнами, обычно ненаблюдаемыми по отдельности. Особенно наглядна физическая картина явления в кристаллах. В них упругие волны одинаковой частоты, бегущие навстречу друг другу, образуют стоячие волны той же частоты, то есть создают периодическую решётку, на которой происходит дифракция света; это явление аналогично дифракции света на ультразвуке. Рассеяние света стоячими волнами происходит по всем направлениям, но, вследствие интерференции света, за рассеяние в данном направлении ответственна упругая волна одной определённой частоты.
Пусть на плоском фронте такой волны рассеиваются, изменяя своё направление на угол  , лучи падающего света частоты , лучи падающего света частоты  (длины волны (длины волны 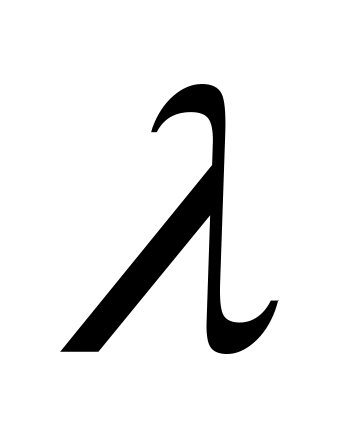 ; ;  , где с* – скорость света в кристалле). , где с* – скорость света в кристалле).
Чтобы рассеянные волны, интерферируя, формировали максимум интенсивности в данном направлении, необходимо, чтобы оптическая разность хода СВ + ВD соседних (1 и 2) падающих и рассеянных (1’ и 2’) волн была равна :
 , (1) , (1)
где 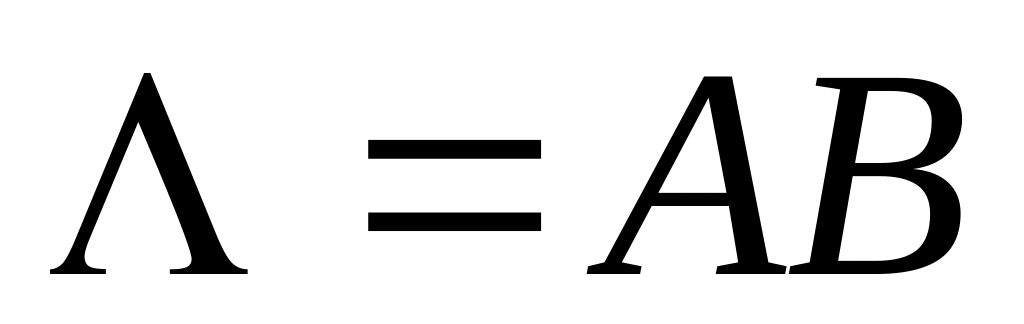 – длина рассеивающей упругой (гиперзвуковой) волны. Рассеяние световой волны на упругой эквивалентно модуляции света падающего пучка с частотой упругой волны. С учётом условия (1) можно получить выражение для относительного изменения частоты рассеянного света: – длина рассеивающей упругой (гиперзвуковой) волны. Рассеяние световой волны на упругой эквивалентно модуляции света падающего пучка с частотой упругой волны. С учётом условия (1) можно получить выражение для относительного изменения частоты рассеянного света:
 , (2) , (2)
где  - скорость упругих волн в кристалле. - скорость упругих волн в кристалле.

Смещение частоты света при рассеянии Мандельштама – Бриллюэна относительно невелико, так как 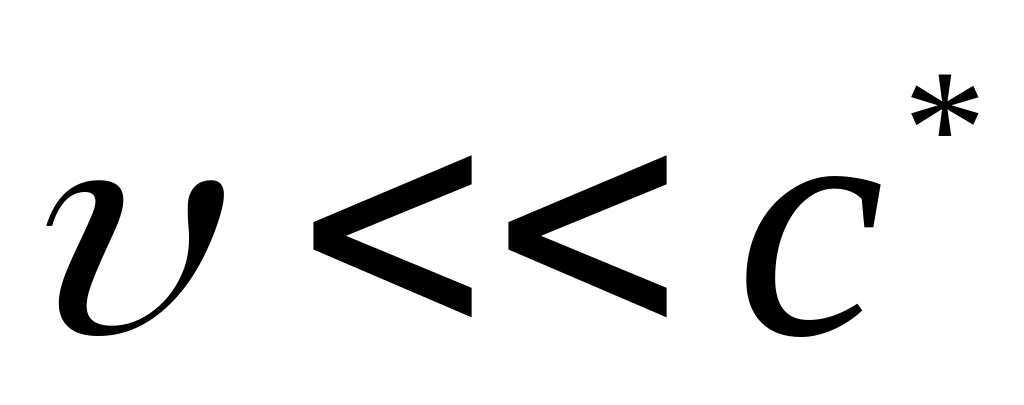 . Например, для кристалла кварца . Например, для кристалла кварца  см/с, с* = 2∙1010 см/с и при рассеянии под углом 90° см/с, с* = 2∙1010 см/с и при рассеянии под углом 90° . Но такие величины надёжно измеряются интерферометрами. . Но такие величины надёжно измеряются интерферометрами.
Из представления о стоячих волнах, модулирующих световую волну, исходил Л.И. Мандельштам, теоретически предсказавший это рассеяние. Независимо от него те же результаты получил французский физик Л. Бриллюэн, рассматривая рассеяние света на бегущих навстречу друг другу упругих волнах в среде. Причиной «расщепления» монохроматических линий в этом случае является эффект Доплера.
Экспериментально рассеяние Мандельштама – Бриллюэна впервые наблюдалось Мандельштамом и Г.С. Ландсбергом (1930). Детально его исследовал Е.Ф. Гросс. В частности, он обнаружил (1938), что при рассеянии Мандельштама – Бриллюэна в кристаллах линия расщепляется на шесть компонентов. Это объясняется тем, что скорость звука в кристалле различны в различных направлениях, вследствие чего в общем случае в нём существует три – одна продольная и две поперечные – упругие волны одной и той же частоты, каждая из которых распространяется со своей скоростью. Гросс изучил также рассеяние Мандельштама – Бриллюэна в жидкостях и аморфных твёрдых телах (1930 – 1932), при котором наряду с двумя смещёнными наблюдается и несмещённый компонент исходной частоты. Теоретическое объяснение этого явления принадлежит Л.Д. Ландау и чешскому физику Г. Плачеку (1934), показавшим, что кроме флуктуаций плотности, необходимо учитывать флуктуации температуры среды.
После создания лазеров не только улучшились возможности для наблюдения рассеяния Мандельштама – Бриллюэна, но и было открыто новое явление – вынужденное рассеяние Мандельштама – Бриллюэна. Оно обусловлено нелинейным взаимодействием интенсивной возбуждающей световой волны (первоначально слабой рассеянной волны) и упругой тепловой волны. Основой такого взаимодействия является эффект электрострикции, заключающийся в том, что диэлектрик в электрическом поле напряжённости Е меняет свой объём и таким образом возникает электрострикционное давление (и следовательно образуется упругая волна), которое прямо пропорционально Е2. В гигантском импульсе лазера напряжённость электрического поля световой волны может достигать значений 104 – 108 В/см, и тогда электрострикционное давление может составить сотни тысяч атмосфер и возникает весьма интенсивный гиперзвук. Интенсивность звуковой волны, возникающей при вынужденном рассеянии Мандельштама – Бриллюэна, невелика.
Применяя исследование рассеяния Мандельштама – Бриллюэна в сочетании с другими методами удаётся получить ценную информацию о свойствах рассеивающей среды. Вынужденное рассеяние Мандельштама – Бриллюэна используется при генерации мощных гиперзвуковых волн в кристаллах.
Список литературы
Гавронская Ю.Ю. Коллоидная химия : Учебник. СПб.: Изд-во РГПУ им. А. И. Герцена, 2007. - 267 с.
Новый политехнический словарь.- М.: Большая Российская энциклопедия, 2000.- .20 с. , 231 с. , 460 с.
Руководство по выполнению экспериментов к «NanoSchoolBox». NanoBioNet e.V/ Scince Park Перевод ИНТ.
https://indicator.ru/article/2016/12/04/istoriya-nauki-chelovek-rasseyanie.
http://kf.info.urfu.ru/fileadmin/user_upload/site_62_6389/pdf/FiHNS_proceedings.pdf
http://www.ngpedia.ru/id623274p1.html
|
|
|
 Скачать 446.83 Kb.
Скачать 446.83 Kb.

 ривая, графически представляющая распределение интенсивности рассеянного света по разным направлениям, называется индикатрисой рассеяния. Если падающий свет естественный, то индикатриса рассеяния света на частицах, малых по сравнению с длиной волны, описывается формулой Рэлея:
ривая, графически представляющая распределение интенсивности рассеянного света по разным направлениям, называется индикатрисой рассеяния. Если падающий свет естественный, то индикатриса рассеяния света на частицах, малых по сравнению с длиной волны, описывается формулой Рэлея: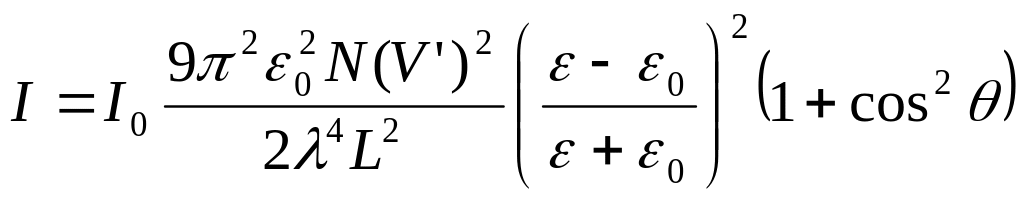 .
. может служить мерой оптической неоднородности среды. При
может служить мерой оптической неоднородности среды. При 
