Лабораторная. Задание Электрическое смещение. Диэлектрическая проницаемость. Теорема Гаусса для диэлектриков. Ответ
 Скачать 65.19 Kb. Скачать 65.19 Kb.
|
|
Лабораторная работа Вариант 6 Задание 1. Электрическое смещение. Диэлектрическая проницаемость. Теорема Гаусса для диэлектриков. Ответ: Напряженность электрического поля, согласно формуле  , зависит от свойств среды. Вектор напряженности переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчете электростатических полей. Поэтому помимо вектора напряженности поле характеризуется вектором электрического смещения или электрической индукции, который для электрически изотропной среды по определению равен: , зависит от свойств среды. Вектор напряженности переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчете электростатических полей. Поэтому помимо вектора напряженности поле характеризуется вектором электрического смещения или электрической индукции, который для электрически изотропной среды по определению равен:  или или  . Единица измерения электрического смещения – Кл/м2. Диэлектрическая проницаемость среды показывает во сколько раз поле ослабляется диэлектриком, характеризуя количественно свойства диэлектрика поляризоваться в электрическом поле . Единица измерения электрического смещения – Кл/м2. Диэлектрическая проницаемость среды показывает во сколько раз поле ослабляется диэлектриком, характеризуя количественно свойства диэлектрика поляризоваться в электрическом поле  . . 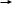 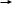 Теорема Остроградского Гаусса. Поток вектора напряженности электрического поля в диэлектрике через замкнутую поверхность S равен алгебраической сумме сторонних и связанных зарядов, охватываемых рассматриваемой поверхностью, деленной на Теорема Остроградского Гаусса. Поток вектора напряженности электрического поля в диэлектрике через замкнутую поверхность S равен алгебраической сумме сторонних и связанных зарядов, охватываемых рассматриваемой поверхностью, деленной на  , т.е. , т.е. 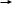 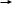 Появление связных зарядов Появление связных зарядов  усложняет дальнейший расчет E по формуле (1). Эту трудность можно обойти, если выразить заряд усложняет дальнейший расчет E по формуле (1). Эту трудность можно обойти, если выразить заряд  через поток вектора Р по формуле: через поток вектора Р по формуле: 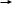 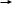 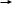 тогда формула (1), после умножения на тогда формула (1), после умножения на  примет вид: примет вид: 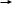 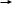 где где Величина, стоящую под интегралом в скобках, обозначается как 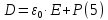 называется вектором электрического смещения. Введение вектора электрического смещения значительно упрощает анализ и расчет электрического поля в диэлектрике. Это связано с тем, что поток вектора D через замкнутую поверхность S равен алгебраической сумме сторонних зарядов, охватываемых данной поверхностью, т.е.  Единицей измерения вектора D в СИ является 1 [Кл/м2] Задание 2. Определить емкость плоского конденсатора, если известна площадь S и расстояние между ними d. Ответ: Емкость плоского конденсатора зависит от площади пластин, расстояния между ними и материала (диэлектрика), заполняющего пространство между пластинами. Тогда в соответствии с формулой емкости, 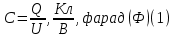 где С – электрическая емкость (Ф), Q – подведенный заряд (Кл), U – потенциал (В). а также формулами поверхностной плотности заряда  где σ – поверхностная плотность заряда, Кл/м2, Q – заряд поверхности проводника, Кл, S – площадь поверхности проводника, м2. и напряженности однородного электрического поля  где Е – напряженность однородного электрического поля (В/м), U — напряжение между пластинами (В), d — расстояние между заряженными пластинами (м). и подставив в формулу (1), получим.  где C – емкость плоского конденсатора (Ф), S – площадь пластин конденсатора (м2), d – расстояние между пластинами (м), ε0 – электрическая постоянная (Ф/м), ε – относительная диэлектрическая проницаемость. Отсюда  Задание 3. Три конденсатора соединены, как показано на рисунке. Какой заряд накормлен всеми конденсаторами? Напряжение, подведенное к точкам А и В равно 250В. Электроемкость С1 = 1,5 мкФ, С2 = 3,0 мкФ, С3 = 4,0 мкФ.      С2 С1         А В С3 Ответ:
Задание 4. Плоский воздушный конденсатор подключили к источнику напряжения и затем отключили от него. После этого сдвинули пластины конденсатора, уменьшив зазор в два раза. Как изменилась при этом объемная плотность энергии электрического поля в конденсаторе? Ответ: Если конденсатор отключен от источника, то его заряд не меняется. Теперь - мы уменьшили зазор, но емкость обратно пропорциональна зазору, следовательно, емкость возрастет в два раза. Энергия конденсатора с зарядом Q обратно пропорциональна емкости, поэтому энергия уменьшится в 2 раза. Плотность энергии не изменится, потому что отношение энергии конденсатора (уменьшилась вдвое) к его объему (уменьшился вдвое) не изменится. Задание 5. Пространство между пластинами заполнено парафином (  ). Расстояние между пластинами d=8,85 мм. Какую разность потенциалов необходимо подать на пластины, чтобы поверхностная плотность связанных зарядов на парафине составляла 0,1 нКл/см2? ). Расстояние между пластинами d=8,85 мм. Какую разность потенциалов необходимо подать на пластины, чтобы поверхностная плотность связанных зарядов на парафине составляла 0,1 нКл/см2?Ответ:
|













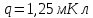









 – электрическая постоянная
– электрическая постоянная 