|
|
Опорный конспект по теме _Определенный интеграл_. Определенным интегралом функции
Интеграл
|
Определенным интегралом функции f(x) от а до b называется число, к которому стремится Snприn, стремящемуся к бесконечности, и обозначается:
 , где а – нижний предел интегрирования, , где а – нижний предел интегрирования,
b – верхний предел интегрирования,
f(x) – подынтегральная функция,
х – переменная интегрирования.
|
Таблица интегралов
|
|
Геометрический смысл интеграла
|
Если функция f(x) непрерывна и неотрицательна на отрезке [a; b], то
интеграл  равен площади соответствующей криволинейной трапеции: равен площади соответствующей криволинейной трапеции:  = S. = S.
|
Формула Ньютона-Лейбница
|
Пусть f(x) – непрерывная функция на отрезке [a; b], F(x) – первообразная этой функции, то  = F(b) – F(a). = F(b) – F(a).
|
Основные свойства интеграла
|
1. 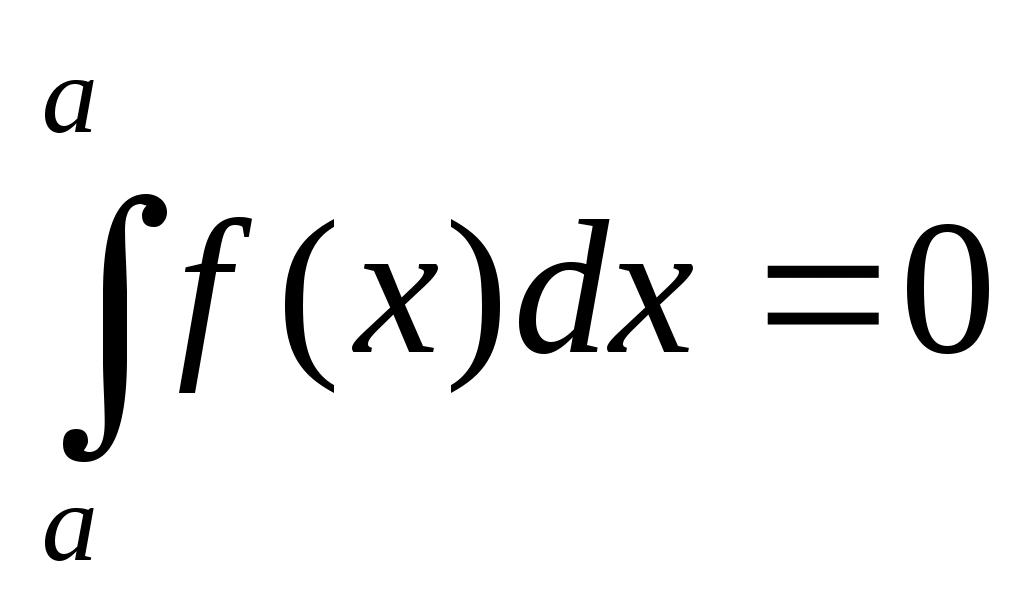 ; 2. ; 2.  ; ;
3. 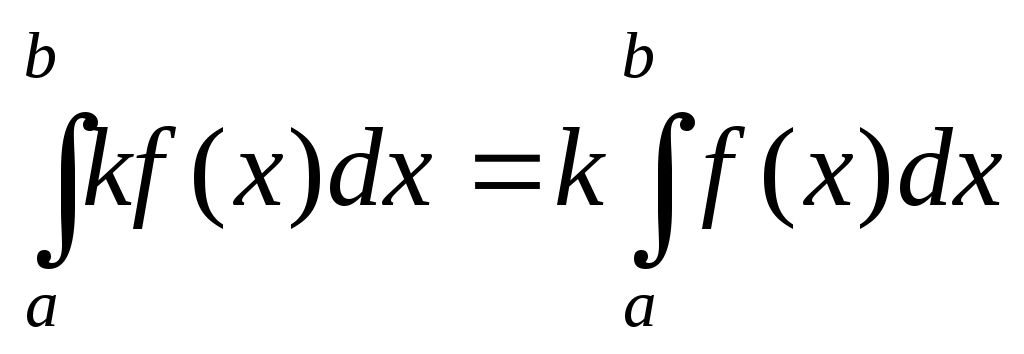 ; 4. ; 4. 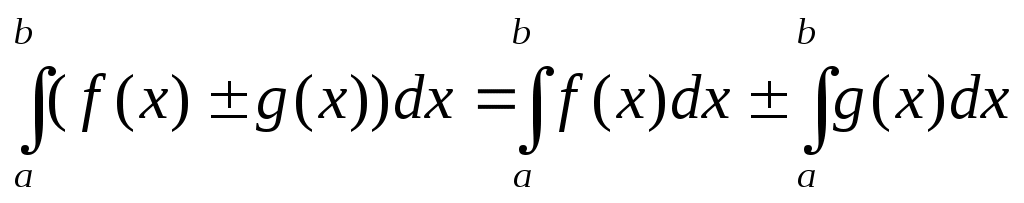
5.  . .
|
Связь между интегралом и площадью
|
1. Если функция f(x) непрерывна и неотрицательна на отрезке [a; b], то
     S = S = . .
|
2 . Если функция f(x) непрерывна и неположительна на отрезке [a; b], то . Если функция f(x) непрерывна и неположительна на отрезке [a; b], то
    S = - S = -  . .
|
3 . Если функция f(x) непрерывна на отрезке [a; b] и ее график пересекает отрезок [a; b] в конечном числе точек, то . Если функция f(x) непрерывна на отрезке [a; b] и ее график пересекает отрезок [a; b] в конечном числе точек, то
   = S1 – S2 + S3 – S4. = S1 – S2 + S3 – S4.
|
4  . Если фигура ограничена графиками непрерывных и неотрицательных на отрезке [a; b] функций f(x) и g(x), прямыми x = a, x = b, y = 0 . Если фигура ограничена графиками непрерывных и неотрицательных на отрезке [a; b] функций f(x) и g(x), прямыми x = a, x = b, y = 0
и    f(x) ≥ g(x), то S = f(x) ≥ g(x), то S = . .
|
Схема решения задач на вычисление площади фигуры
|
Изобразите чертеж фигуры, площадь которой нужно найти.
Если одна ил обе прямые x = a, x = b, ограничивающие фигуру, не заданы, то найдите абсциссы точек пересечения графиков функций f(x) и g(x), реши уравнение f(x) = g(x).
Найдите площадь фигуры по соответствующей формуле.
|
Интеграл
|
Определенным интегралом функции f(x) от а до b называется число, к которому стремится Snприn, стремящемуся к бесконечности, и обозначается:
 , где а – нижний предел интегрирования, , где а – нижний предел интегрирования,
b – верхний предел интегрирования,
f(x) – подынтегральная функция,
х – переменная интегрирования.
|
Таблица интегралов
|
|
Геометрический смысл интеграла
|
Если функция f(x) непрерывна и неотрицательна на отрезке [a; b], то
интеграл  равен площади соответствующей криволинейной трапеции: равен площади соответствующей криволинейной трапеции:  = S. = S.
|
Формула Ньютона-Лейбница
|
Пусть f(x) – непрерывная функция на отрезке [a; b], F(x) – первообразная этой функции, то  = F(b) – F(a). = F(b) – F(a).
|
Основные свойства интеграла
|
. 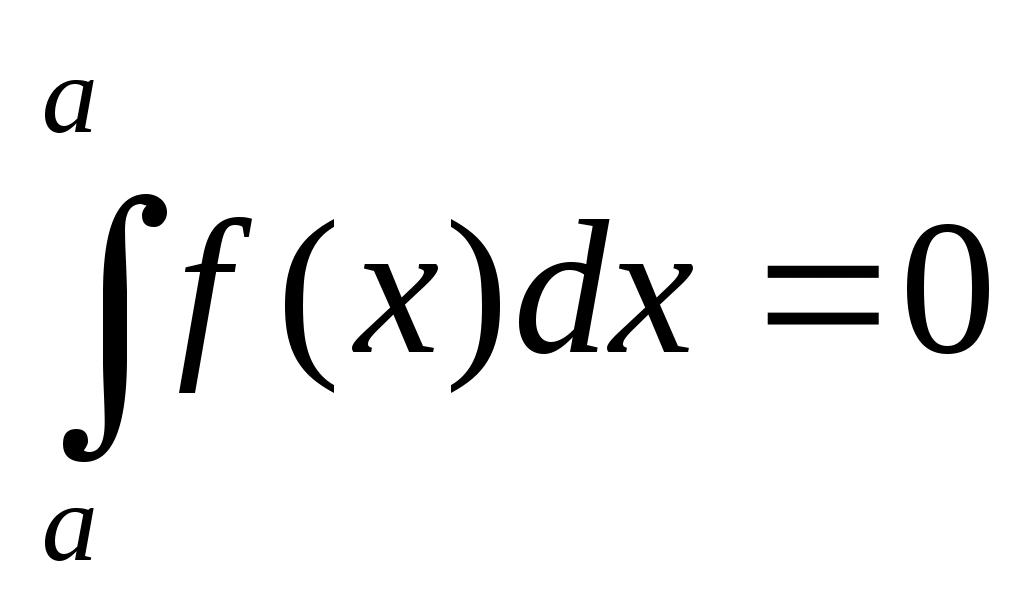 ; 2. ; 2.  ; ;
3. 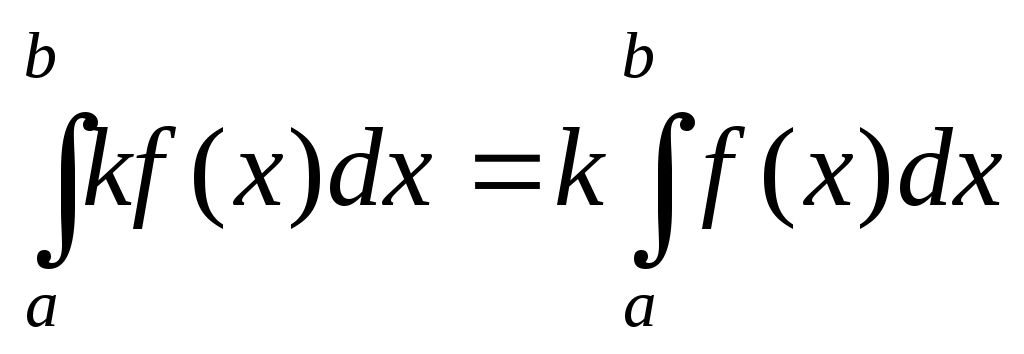 ; 4. ; 4. 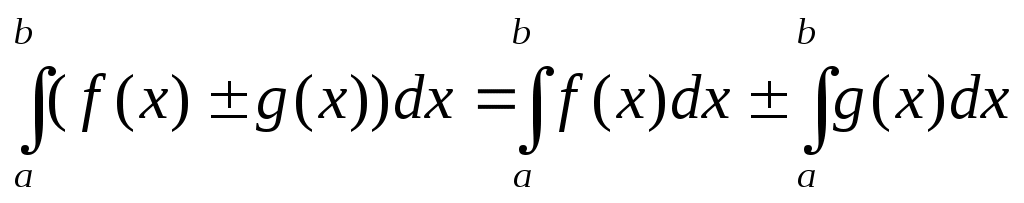
5.  . .
|
Связь между интегралом и площадью
|
1. Если функция f(x) непрерывна и неотрицательна на отрезке [a; b], то
     S = S = . .
|
2 . Если функция f(x) непрерывна и неположительна на отрезке [a; b], то . Если функция f(x) непрерывна и неположительна на отрезке [a; b], то
    S = - S = -  . .
|
3 . Если функция f(x) непрерывна на отрезке [a; b] и ее график пересекает отрезок [a; b] в конечном числе точек, то . Если функция f(x) непрерывна на отрезке [a; b] и ее график пересекает отрезок [a; b] в конечном числе точек, то
   = S1 – S2 + S3 – S4. = S1 – S2 + S3 – S4.
|
4  . Если фигура ограничена графиками непрерывных и неотрицательных на отрезке [a; b] функций f(x) и g(x), прямыми x = a, x = b, y = 0 . Если фигура ограничена графиками непрерывных и неотрицательных на отрезке [a; b] функций f(x) и g(x), прямыми x = a, x = b, y = 0
и    f(x) ≥ g(x), то S = f(x) ≥ g(x), то S = . .
|
Схема решения задач на вычисление площади фигуры
|
Изобразите чертеж фигуры, площадь которой нужно найти.
Если одна ил обе прямые x = a, x = b, ограничивающие фигуру, не заданы, то найдите абсциссы точек пересечения графиков функций f(x) и g(x), реши уравнение f(x) = g(x).
Найдите площадь фигуры по соответствующей формуле.
| |
|
|
 Скачать 93.5 Kb.
Скачать 93.5 Kb.