математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
ts - 58,13 Среднее число заявок в системе (среднее число занятых каналов) можно вычислить через вероятности Po, Pj, ■■■, PkPn, по формуле ns -0• Р0 +1-р +... + n• Pn (9) как математическое ожидание дискретной случайной величины. Однако, проще выразить среднее число занятых каналов через абсолютную пропускную способность А, которая уже известна. Действительно, А есть среднее число заявок, обслуживаемых в единицу времени; один занятый канал обслуживает в среднем / заявок в единицу времени; среднее число занятых каналов получается делением А на u - = a=яа-р) U j или, переходя к обозначению р = — : U nS =Р(\ - Pn ) Посмотрим, как может применяться описанная модель для решения оптимизационной задачи проектирования системы. Пускай нам требуется определить наиболее предпочтительный (в смысле экономического эффекта) вариант многоканальной СМО с отказами. Для этого необходимо определить число обслуживающих приборов n, при котором достигается максимум функции P = I - C , (10) n n n ' V / где P - величина получаемой прибыли; In - получаемый в результате эксплуатации системы доход; C - стоимость эксплуатации приборов (все величины приведены к единице времени). Будем искать решение при таких предположениях: средний интервал времени между заявками в потоке (ta) составляет 5 мин; заявка обрабатывается в среднем 5 мин (ts); затраты на эксплуатацию одного прибора (C) составляют 1 рублей/мин; доход от одной обслуженной заявки (I) равен 80 рублей. Значение функции I(n) находится как произведение величины абсолютной пропускной способности на величину дохода от обслуживания одной заявки: Т = A ■ I n n Значение функции C находится как произведение затрат на эксплуатацию одного прибора на число приборов: Сп = С ■ п P = Т — С Поэтому, подставляя в п Тп Сп > (10), получаем F(0, 02, ... , вп) = P(Ti <01, 7*2 <^2, ... , 7 <вп) , 21 tk = k \ k , k = 1,2,...,6 28 fT ' 29 у2 _ У1 (f к - fk) 29 Лнабл / , rT ' 29 Pk =^p0,k = 1,2- n 84 л — — — — — — 84 — 84 Проверка графа модели. 196 Вопросы для самопроверки: 197 Литература по теме: 197 Вопрос 2. Узловые операторы. 201 Вопрос 3. Текст программной модели СМО. 202 Вопрос 4. Сборка и запуск исполнительного модуля модели. 205 File \cnv-> Projects -> Win32 Application. 206 • Build Execute ModelPro.exe. 207 Вопрос 5. Результаты моделирования. 208 Вопросы для самопроверки: 211 3.Какую функцию выполняет предложение #include ? 211 term? 211 Литература по теме: 211 Вопрос 2. Использование узла parent. 215 Вопрос 3. Использование узлов pay, rent, down. 216 Вопрос 4. Многослойная модель бизнес-процесса. 219 Выводы: 225 Вопросы для самопроверки: 226 Литература по теме: 226 Вопрос 2. Определение нестандартных выходных параметров. 230 Вопрос 3. Отладка модели. 233 Вопрос 4. Построение гистограмм. 235 Вопросы для самопроверки: 240 Литература по теме: 240 Вопрос 2. Отсеивающий эксперимент 246 F"=! F 249 Вопрос 33. Аналитическое описание функции отклика. 250 ■ n(n - l)(n - 2)...(n - i -1) 251 1-2 • ....i 251 , 4 • 3 • 2 251 4 1-2 • 3 251 b + bx + bx +... + bx = bx + bx + bx +... + bx =V bx 251 Вопрос 4. Поиск оптимальных значений. 253 Выводы: 254 Вопросы для самопроверки: 255 Приложение 255 Узловые операторы системы Pilgrim 255 Далее по формуле A = 1- q (3) находим величину абсолютной пропускной способности для нескольких значений n: n=1: И q=Po = По формуле 1 + И (2) находим q 1 q=гЧ - 5 5 и по формуле A =1 ■q (3) A 1 A = = 0,1мин 1 +1 5 5 n=2: okP Pk =PP°, k = 1,...n p По формулам k! (5) находим сначала 0 po=-h2=0'4 1 ^ —+ — 1! 2! затем по формуле (6) Рог 12 P - —0,4 = 0,2 отк 2| ' и по формуле A -1q -1(1" Pn) (8) A A -1(1 -0,2) - 0,16мин- Аналогично получаем: n=3: P Ц г - 0,375 ° 1 12 13 1 +—+—+— 1! 2! 3! 13 Ротк - ^0,38 - 0,0625 A -1(1 - 0,0633) - 0,1875мин- n=4: P0 о 1 12 13 14 1 1! 2! 3! 4! 14 Ротк - —0,3692 - 0,0154 A -1 (1 - 0,0154) - 0,1969мин- n=5: P0 о 1 12 13 14 15 1 ч 1 1 1 1— 1! 2! 3! 4! 5! P = A • I - C • n (11) n n Ротк = -0,3681 = 0,0031 A = 1(1 - 0,0031) = 0,1994мин Подставляя найденные значения в находим: P = 7,0 руб / мин P2 = 10,8 руб / мин P = 12,0 руб / мин P4 = 11,75 руб / мин P5 = 10,95 руб / мин График зависимости P от n имеет вид: 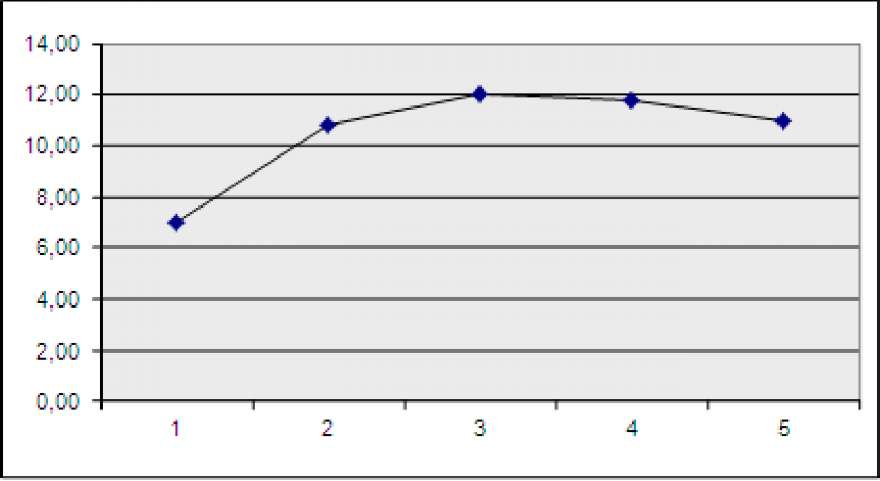 Рис. 18. Зависимость величины приведенной прибыли от числа приборов Как видим, максимум прибыли в единицу времени достигается для числа обслуживающих приборов равного трем. Вопрос 4. Обслуживание с очередями. В системах с ожиданием заявки, заставшие обслуживающий прибор в момент прихода занятым, в отличие от систем с отказами не покидают систему, а остаются ждать в очереди вместе с другими ждущими заявками (рис. 15). Для описания таких систем используются показатели, характеризующие длину очереди и время ожидания заявками обслуживания. В частности, если временной интервал между появлением заявок распределен по экспоненциальному закону (пуассоновский поток), то среднее время ожидания заявки в очереди tw можно найти по формуле Хинчина-Полачека: tw 2(1 -р) ' ( ) где ts — среднее время обслуживания заявки; as — среднеквадратическое (стандартное) отклонение времени обслуживания в приборе; р — коэффициент использования прибора = —; ta j t a — средний интервал времени между поступлением заявок; cs — коэффициент вариации времени обслуживания <. t s Число заявок, ожидающих обслуживания (среднюю длина очереди), можно найти, умножив tw на величину к. -п, = — .-,„ = 2(1 -P) ( ) что, с учетом равенства — ■ tw = P дает п, 2(1 -P) ( ) Формула Хинчина-Полачека используется для оценивания длин очередей при проектировании информационных систем. Она применяется в случае экспоненциального распределения времени поступления при любом распределении времени обслуживания и любой дисциплине управления, лишь бы выбор очередного сообщения для обслуживания не зависел от времени обслуживания. При проектировании систем встречаются такие ситуации возникновения очередей, когда дисциплина обслуживания выбирается в зависимости от времени обслуживания. Например, в некоторых случаях для первоочередного обслуживания могут выбираться более короткие сообщения с тем, чтобы получить меньшее среднее время обслуживания (среднее время пребывания в заявки системе). При управлении линией связи (каналом Интернет) можно присвоить входным сообщениям более высокий приоритет, чем выходным, поскольку первые короче. В таких случаях уже необходимо использовать не уравнение Хинчина — Поллачека или производные от него, а более сложные уравнения или использовать метод имитационного моделирования, рассматриваемы далее. Особый интерес для практических применений представляют два случая. 1) Время обслуживания постоянно. При регулярном характере потока рассеяние отсутствует, поэтому среднеквадратическое отклонение cs = 0, и формулы (12), (13) преобразуются в выражения -„, = (15) 2(1 -р) 2(1 -р) ( ) и tw = (16) 2(1 -р) ( ) 2) Время обслуживания имеет экспоненциальное распределение. В случае экспоненциального распределения, как известно, среднеквадратическое отклонение cs= 1, поэтому (12), (13) принимают вид: |
