математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
|
плотности вероятностей, или интенсивности перехода Aif из состояния Si в состояние S,-. Пусть система S в момент t находится в состоянии Sr. Рассмотрим элементарный промежуток времени At, примыкающий к моменту t. Назовем плотностью вероятности перехода Aif из состояния i в состояние j предел отношения вероятности перехода системы за время At из состояния Si в состояние S, к длине промежутка At: х= ]im p„(t + At) - pj(t) _ [im p(AO, (3) J At->0 At A-0 fat где Pj(At) — вероятность того, что система, находившаяся в момент t в состоянии Si за время At перейдет из него в состояние Sj (плотность вероятностей перехода определяется только для j^-i). pj (t + At) - pj TT ] At-o At At-° At Из (3) следует, что при малом At вероятность перехода (с точностью до бесконечно малых высших порядков) равна: Pj(At)=Aj At Если все плотности вероятностей перехода Aif не зависят от t (от того, в какой момент начинается элементарный участок At) P{S(t + At) _ S | S(t) _ j}, i_\n, J _ 1n, то марковский процесс называется однородным, в противном случае - неоднородным. Предположим, что известны плотности вероятностей перехода Aif для всех пар состояний Si,Sf. ГСП системы с проставленными у стрелок плотностями вероятностей перехода называется размеченным графом состояний (рис. 11), на основании которого можно определить вероятности состояний pi(t) как функции времени р(0 _ (p1(t), p(t ),■■■, Pn (t)) (2). 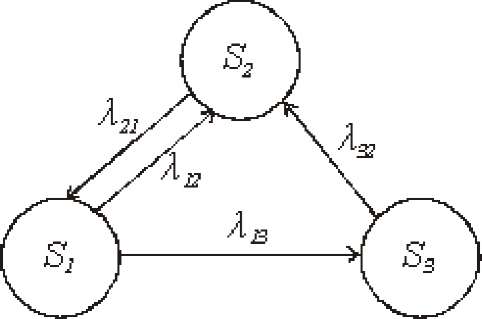 Рис. 11' Пример размеченного графа состояний и переходов Вопрос 2. Уравнения Колмогорова. Если протекающий в системе случайный процесс является марковским процессом с непрерывным временем, то для вероятностей p(t), p2(t), ■■■ pw(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова. Покажем, как получаются эти уравнения на примере ГСП рис 11. Рассмотрим вначале вершину графа Sx - Вероятность p (t + At) того, что система в момент времени (t + At) окажется в состоянии Sj, определяется на основе рассмотрения трех возможностей попасть в это состояние: Система в момент времени t с вероятностью p (t) находилась в состоянии Sj и за малое время At не перешла в состояние S2' Из состояния S система может быть выведена потоком интенсивностью \2' Вероятность выхода системы из состояния S за время At с точностью до величин более высокого порядка малости по At равна ^2At, а вероятность сохранения состояния S будет равна 1 - ^2At' При этом вероятность того, что система останется в состоянии S , согласно теореме об умножении вероятностей будет равна p (t )(1 - ^2At)' цвероятностью ^At. Вероятность того, что система будет находиться в состоянии S, равна p3 (t )\xAt. По теореме сложения вероятностей получим: Px(t + At) = P1(t)(1 — ^At) + P2(t)llxSt + РзО)Х,хЫ Px(t + At) — px(f) = px(t)\2At + p1(t)llxAt + P3(f)XiXAt и, переходя к пределу At ^ 0, dP1(t) _ ^ |
