математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
|
вероятностями состояния. Для любого шага (момента времени t1, t2, ... tk, ... или номера 1, 2, ... , к, ...) существуют некоторые вероятности перехода системы из любого состояния в любое другое (некоторые из них равны нулю, если непосредственный переход за один шаг невозможен), а также вероятность задержки системы в данном состоянии. Эти вероятности называются переходными вероятностями марковской цепи. Если значения переходных вероятностей не зависят от номера шага, то марковская цепь называется однородной, или стационарной. В противном случае марковская цепь является неоднородной, или нестационарной. Если из состояния Si не исходит ни одной стрелки (переход из него ни в какое другое состояние невозможен, например, S3 графа рис. 8), соответствующая вероятность задержки Pii равна единице. Графу системы, содержащему n вершин, можно поставить в соответствие матрицу n*n, элементами которой являются вероятности переходов pj между вершинами графа, называемую матрицей вероятностей переходов: R р 11 и In P P 12 Р р PP 21 2 J 2п -i гул ± п 22 (1) PP р1 р2 р:, Р,- P = (P) PP ii. Р„ р n1 р n2 Элементы матрицы переходов, означающие вероятности переходов в системе за один шаг, удовлетворяют условиям: 0 < ptj < 1 (2) n I pj =1 (3) j=1 Условие (2) выражает ограничение, накладываемое на значение вероятности, а условие (3) означает, что система S обязательно либо переходит из какого-то состояния Si в другое состояние, либо остается в состоянии Si (иначе говоря, события S(kS(kS(kS(к) образуют полную группу событий). Обычно на графе вероятности перехода системы из одного состояния в то же самое не отмечаются, так как каждая из них дополняет до единицы сумму переходных вероятностей, соответствующих всем стрелкам, исходящим из данного состояния. Например, для графа рис. 8 б значения переходных вероятностей Pu будут равны: Pi = 1 - (P2 + Рз) Р22 = 1 — (Р23 ^ Р24 ^ Р25 ) Рзз= 1 Р = 1 — Р 1 44 1 1 45 Р = 1 — Р 1 55 1 Р 53 . При рассмотрении конкретных систем удобно сначала построить граф состояний, затем определить вероятность переходов системы из одного состояния в то же самое (исходя из требования равенства единице суммы элементов строк матрицы), а потом составить матрицу переходов системы. Имея размеченный ГСП (или, что равносильно, матрицу переходных вероятностей) и зная начальное состояние системы, можно найти вероятности состояний р1(к), р2(к), ... , рп(к) после любого (к-го) шага. Они находятся с помощью следующих рекуррентных соотношений: n P(k) = ^Pj(k — 1)Р (i = 1,...n) (4) j =1 или в матричной форме р(к)=р(Ы)хР, (5) где р(к), р(к-1) - матрицы-строки вероятностей состояний после к-го и (к-1)-го шагов соответственно; Р - матрица переходных вероятностей. Предположим, что в начальный момент (перед первым шагом) система находится в каком-то определенном состоянии, например Sm. Тогда для начального момента (0) будем иметь: Pl(0) =0, Р2(0) =0, ''', Pm(0) = 1, ''' , Pn(0) = 0, т. е. вероятности всех состояний равны нулю, кроме вероятности начального состояния Sm, равной единице. Найдем вероятности состояний после первого шага. Мы знаем, что перед первым шагом система заведомо находится в состоянии Sm. Значит, за первый шаг она перейдет в состояния S1, S2, — , Sm, — , Sn с вероятностями Pm1, Pm2, ''' , Pmm, ''' , Pmn , находящимися в m-ой строке матрицы переходных вероятностей. Таким образом, вероятности состояний после первого шага будут: Pl(1) _ Pml, Р2 (1) _ Pm2, -, Pm (1) _ Pm, ■■■, Pn (1) _ P„n (6) Найдем вероятности состояний после второго шага: p(2) _ (p1(2), p2(2),...,рг(2),...,pn(2)). Вычислим их по формуле полной вероятности с гипотезами: после первого шага система была в состоянии S1; после первого шага система была в состоянии S2; после первого шага система была в состоянии Si; после первого шага система была в состоянии Sn. Вероятности гипотез известны (6), условные вероятности перехода в состояние Si - при каждой гипотезе тоже известны и записаны в матрице переходных вероятностей. По формуле полной вероятности получим:
или n F(0, 02, ... , вп) = P(Ti <01, 7*2 <^2, ... , 7 <вп) , 21 tk = k \ k , k = 1,2,...,6 28 fT ' 29 у2 _ У1 (f к - fk) 29 Лнабл / , rT ' 29 Pk =^p0,k = 1,2- n 84 л — — — — — — 84 — 84 Проверка графа модели. 196 Вопросы для самопроверки: 197 Литература по теме: 197 Вопрос 2. Узловые операторы. 201 Вопрос 3. Текст программной модели СМО. 202 Вопрос 4. Сборка и запуск исполнительного модуля модели. 205 File \cnv-> Projects -> Win32 Application. 206 • Build Execute ModelPro.exe. 207 Вопрос 5. Результаты моделирования. 208 Вопросы для самопроверки: 211 3.Какую функцию выполняет предложение #include ? 211 term? 211 Литература по теме: 211 Вопрос 2. Использование узла parent. 215 Вопрос 3. Использование узлов pay, rent, down. 216 Вопрос 4. Многослойная модель бизнес-процесса. 219 Выводы: 225 Вопросы для самопроверки: 226 Литература по теме: 226 Вопрос 2. Определение нестандартных выходных параметров. 230 Вопрос 3. Отладка модели. 233 Вопрос 4. Построение гистограмм. 235 Вопросы для самопроверки: 240 Литература по теме: 240 Вопрос 2. Отсеивающий эксперимент 246 F"=! F 249 Вопрос 33. Аналитическое описание функции отклика. 250 ■ n(n - l)(n - 2)...(n - i -1) 251 1-2 • ....i 251 , 4 • 3 • 2 251 4 1-2 • 3 251 b + bx + bx +... + bx = bx + bx + bx +... + bx =V bx 251 Вопрос 4. Поиск оптимальных значений. 253 Выводы: 254 Вопросы для самопроверки: 255 Приложение 255 Узловые операторы системы Pilgrim 255 суммирование распространяется формально на все состояния Sj, S2, ... , Sm, ... , Sn ; фактически учитывать надо только те из них, для которых переходные вероятности Pj отличны от нуля, т.е. те состояния, из которых может совершиться переход в состояние Si (или задержка в нем). Таким образом, вероятности состояний после второго шага известны. Очевидно, после третьего шага они определяются аналогично: n Pi■ (3) = Х Pj (2)Pji (i = 1,.n) (10) j =1 И вообще после k-то шага: n Pt(k) = SPj(k - 1)Pi (i = 1,.n) (11) j=1 Или в матричной форме p(k) = p(kA) х p (12) Таким образом, вероятности p (k) состояний после k-го шага п(к) = p(k-1) х p определяются рекуррентной формулой p p 1 (12) через вероятности состояний после (к - 1)-го шага; последние, в свою очередь, — через вероятности состояний после (к - 2)-го шага, и т. д. Например, пусть требуется найти вероятность перехода системы из состояния Si в состояние S2 за 3 шага для графа на рис. 9. 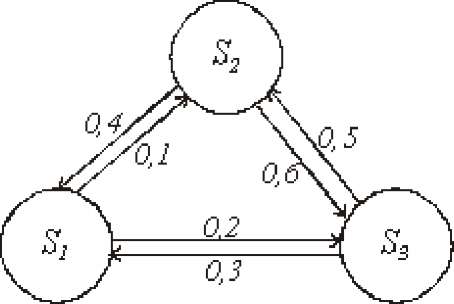 Рис. 9. Пример ГСП Из условия следует, что p (0) = 1, p2 (0) = 0, p3 (0) = 0 . Находим вероятности состояния после первого шага: А(1) = 0,7 p2(1) = 0,1 ps(1) = 0,2 Вероятности состояния после второго шага: p (2) = p (1)p 1 + p2 (1) p21 + p3 (1) p31 = 0,7 • 0,7 + 0,1 • 0,4 + 0,2 • 0,2 = 0,57 p2(2) = p1(1) p12 + p2(1) p22 + p3(1) p32 = 0,7 • 0,1 + 0,1 0,0 + 0,2 • 0,5 = 0,17 p3 (2) = p (1) p3 + p2 (1) p23 + p3 (1) p33 = 0,7 • 0,2 + 0,1 0,6 + 0,2 • 0,3 = 0,26 Вероятность состояния S2 после третьего шага p2 (3): p2 (3) = p (2) p 2 + p2 (2) p^ + p3 (2) p^ = 0,57 • 0,1 + 0,17 • 0,0 + 0,26 • 0,5 = 0,187 Если обозначить через P( m) матрицу, элементами которой являются вероятности переходов из Sj в Sj за m шагов p\™) , то справедлива формула: р(m) _ pm где матрицаPm получается умножением матрицы P саму на себя m раз. Пусть исходное состояние системы задается вектором p(0): Р(0) _ (Pi, Pi,-, Pn где Pi, i=1, ... « есть вероятность того, что в начальный момент система находится в состоянии Si. (13) Тогда для нахождения вектора вероятностей состояния системы после m шагов можно воспользоваться формулой: (14) P (т) — p(°) х р(т) Воспользуемся приведенными формулами для нахождения вектора состояния системы, изображенной рис. 9, после двух шагов, для случая, когда исходное состояние системы задается вектором p(0) _ (0,7; 0;0,3). p(k) _ _(А-1) х р p(1)=p(0)xp=(0,7;0;0,3) ■ С помощью формулы p p р (12) находим сначала состояние системы после первого шага P "0,7 0,1 0,2" 0,4 0 0,6 0,2 0,5 0,3 (0,7 • 0,7 + 0,0 • 0,4 + 0,3 • 0,2; 0,7 • 0,1 + 0,0 • 0,0 + + 0,3 • 0,5; 0,7 • 0,2 + 0,0 • 0,6 + 0,3 • 0,3) _ _ (0,55;0,22;0,23) (2)
и состояние системы после второго шага p (0,519;0,17;0,311) p(m) _ p(0) x Pm) Тот же результат получается с помощью формулы р р (14). Вычислив предварительно величину элементов матрицы
|
