математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205

• Название: Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
• Анкор: математическое моделирование
• Дата: 02.06.2022
• Размер: 1.51 Mb.
• Имя файла: Т 1 МАТ. Моделирование.docx
• Тип: Литература; #564707
• страница: 6 из 31

р(2) =




находим:

p⁽²⁾ =p^{(0) X}P⁽²⁾ =(0,7;0,0;0,3) ■

(0,519;0,17;0,311)
0,57 0,17 0,26" 0,4 0,34 0,26 0,4 0,17 0,43

Вопрос 5. Предельные вероятности цепи Маркова.

Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими. Если при некотором n все элементы матрицы Р не равны нулю, то такая матрица переходов называется регулярной. Другими словами, регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через n шагов из любого состояния. Такие цепи Маркова так же называются регулярными.

Известно (теорема о предельных вероятностях), что для регулярной цепи Маркова с n состояниями и матрицей вероятностей перехода Р существует предел

limP⁽ⁿ⁾ _ P

и матрица P⁽»⁾ имеет вид:

P1 P2 p1 P2

pn pn

P^(m)=

p1 p2 ■■■ pn

т.е. состоит из одинаковых строк.

Величины pi, p2, ...	, Pn	называются предельными
вероятностями. Эти вероятности не зависят от исходного состояния
системы, и вектор вероятности полностью определяется из условий:
n p = p X Р (или p. = IPjPji ) j=1
и условия нормировки
IP. = 1
Пусть требуется найти предельные					вероятности для матрицы
переходов
Р =	" 0,1 0,9" 0,3 0,7_
Так как p + p2 = 1, получаем:
P1 = 0,1P + 0,3P2
P2 = 0,9P + 0,7 P2
P1 + 3 P1 =1
p = 0,25
P2 = 0,75
и матрица предельных вероятностей:
p^ =	"0,25 0,75" 0,25 0,75_
Выводы:
1. Решение многих задач, связанных с анализом процессов и
создания систем, основано на рассмотрении протекающих процессов как
стохастических. Для оценивания показателей этих процессов и систем
применяются аналитические модели.
	57

2. 
   Важным классом случайных процессов является марковский процесс. Марковские процессы протекают в отсутствие предыстории, что значительно упрощает их математическое описание.
   
3. 
   Для описания процесса с дискретным временем и дискретными состояниями используются граф переходов и состояний, а также связанная с ним матрица переходных вероятностей. На основе этих элементов можно найти вероятности нахождения процесса в каждом из своих состояний после любого шага, для чего применяются рекуррентные или матричные выражения, которые получены на основе формулы полной вероятности.
   
4. 
   В случае регулярных цепей Маркова процесс обладает предельными вероятностями нахождения в каждом из своих состояний. Эти вероятности не зависят от номера шага и могут быть найдены путем решения системы линейных уравнений, получаемой из выражения для предельных вероятностей и нормировочного условия.
   

Вопросы для самопроверки:

1. 
   Что такое стохастическая система?
   
2. 
   Какой процесс называется марковским?
   
3. 
   Как классифицируются марковские процессы?
   
4. 
   Дайте определение марковского процесса с непрерывным временем и дискретными состояниями.
   
5. 
   Что такое однородный марковский процесс?
   
6. 
   Что такое граф состояний и переходов (ГСП) Марковской цепи? Какие бывают ГСП?
   
7. 
   Что понимается под матрицей переходных вероятностей?
   
8. 
   Как можно найти вероятность нахождения процесса в определенном состоянии после определенного числа шагов?
   
9. 
   Что такое нестационарная марковская цепь?
   
10. 
    Что такое предельные вероятности марковского процесса?
    
11. 
    Каков физический смысл предельных вероятностей?
    
12. 
    При каких условиях существуют предельные вероятности состояний марковского процесса?
    
13. 
    Как найти предельные вероятности системы, имеющей стационарный режим?
    

Литература по теме:

1. 
   Емельянов А.А., Власова Е.А., Дума Р.В. Имитационное моделирование экономических процессов / Под ред. А.А. Емельянова. - М.: Финансы и статистика, 2009. - 480 с.
   
2. 
   Теория систем и системный анализ в управлении организациями: Справочник / Под ред. В.Н. Волковой и А.А. Емельянова. - М.: Финансы.
   
3. 
   Саати Т.Л. Элементы теории массового обслуживания и её приложения. - М.: Радио и связь, 1965. - 512 с.
   

Тема 5. Непрерывные марковские процессы

Цели изучения темы:

• 
  познакомиться с математическим аппаратом аналитического моделирования непрерывных марковских процессов;
  

Задачи изучения темы:

• 
  изучить математический аппарат описания марковских процессов;
  
• 
  научиться находить характеристики процесса с помощью уравнений Колмогорова.
  

Успешно изучив тему, Вы:

получите представление о:

• 
  как построить математическую модель непрерывного марковского процесса;
  
• 
  что такое стационарный режим и предельные вероятности;
  
• 
  как найти вероятности нахождения марковского процесса в своих состояниях;
  
• 
  что такое процесс гибели и размножения и как он используется для моделирования практических задач.
  

будете знать:

• 
  как описать непрерывно протекающие процессы с помощью графа состояний и переходов;
  
• 
  что такое интенсивности перехода процесса;
  
• 
  как составить уравнения Колмогорова по графу состояний и переходов;
  
• 
  как применить аппарат теории марковских процессов к практическим задачам построения систем.
  

Вопросы темы:

1. 
   Описание непрерывных цепей Маркова.
   
2. 
   Уравнения Колмогорова.
   
3. 
   Процессы гибели и размножения.
   

Вопрос 1. Описание непрерывных цепей Маркова.

Рассмотрим пример. Пусть имеем систему S, включающую один компьютер, который может находиться в одном из пяти возможных состояний:

51. 
    — исправен, работает;
    
52. 
    — неисправен, ожидает осмотра;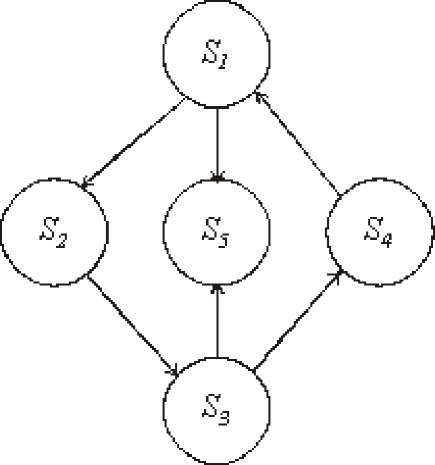
    

Рис. 10. Граф состояний и переходов процесса поломок и

восстановлений




В примере на рис. 10 выход из строя (отказ) компьютера и окончание его ремонта (восстановление) могут произойти в заранее неизвестный момент. Для описания таких процессов может быть применена схема марковского случайного процесса с дискретными состояниями и непрерывным временем. Процессы такого типа известны как непрерывные цепи Маркова. Непрерывной цепью Маркова (марковским процессом) называется процесс, для которого при 0 < t < t₂ < ... < t_w+1 выполняется:

P{S(tn+1) = Sn+11 S(О = S1,... S(tn) = Sn} = P{S(tn+1) = Sn+11 S(t_n) = Sn}

Здесь рассматривается ряд дискретных состояний: S_h S₂, S₃, ..., S_n, однако переход системы S из состояния в состояние может происходить в произвольный момент времени.

Обозначим через pi(t) вероятность того, что в момент t система S будет находиться в состоянии S_i (i= 1, ... , n). Очевидно, для любого момента t сумма вероятностей состояний равна единице:

n

Ежо=1 ⁽¹⁾

2=1

53. 
    — осматривается;
    
54. 
    — ремонтируется;
    
55. 
    — списан.
    

ГСП системы показан на рис. 10.
Так как события, состоящие в том, что в моментt система находится в состоянияхS₁, S₂, ..., S_n, несовместны.

Необходимо определить для любого t вероятности состояний:

p(t) _ (p_l(t), p_l(t),..., p_n (t)) ⁽²⁾

Для того чтобы найти эти вероятности, необходимо знать характеристики процесса. Поскольку вероятность перехода системы из состояния в состояние точно в момент t будет равна нулю (так же как вероятность любого отдельного значения непрерывной случайной величины), то в качестве характеристик процесса рассматриваются