СМО лаб работа 1. СМО ЛР № 1 — копия. Задание Используя программу mkv смоделировать марковский процесс согласно данным индивидуального задания. Определить период устойчивого режима функционирования системы и предельные вероятности состояний.
 Скачать 266.21 Kb. Скачать 266.21 Kb.
|
|
Задание Используя программу MKV смоделировать марковский процесс согласно данным индивидуального задания. Определить период устойчивого режима функционирования системы и предельные вероятности состояний. Построить графики зависимости вероятностей состояний от времени (числа шагов). Объяснить особенности протекания процесса в системе. Постановка задачи Случайный процесс, протекающий в системе S, называется марковским, если для каждого момента времени t0 вероятность любого состояния системы в будущем (при t> t0) зависит только от ее состояния в настоящем (при t = t0) и не зависит от того, когда и каким образом система пришла в это состояние. Каждое состояние S1, S2, S3, ... можно изобразить схематично прямоугольником, а возможные переходы за один шаг — стрелкой. Такие графические схемы называются графами состояний. Случайный процесс называется процессом с непрерывным временем, если переход из одного состояния в другое возможен в любой момент времени. Для любого дискретного момента времени t1, t2, ... существует вероятность перехода системы из одного состояния в другое (переходные вероятности). Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага, в противном случае — неоднородной. Однородная марковская цепь, имеющая n состояний будет содержать вероятность перехода Pij из Si в Sj (Pij не зависит от k), Pii — вероятность задержки в состоянии Si. Существуют ij, для которых Pij = 0. Используя события 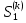 , можно Pij записать в виде , можно Pij записать в виде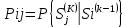 . .Вероятности состояний Pi (k) после k - го шага определяются рекуррентной формулой через вероятности состояний после (k –1) шага 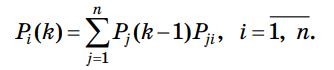 Для неоднородной цепи Маркова 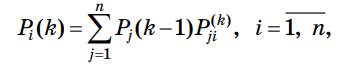 где — вероятность перехода системы из состояния Si в состояние Sj на k - м шаге Исходные данные Динамический процесс в каждый момент времени может находиться в одном состоянии: S1, S2, S3 или S4. В начальный момент он находится в состоянии S1. Матрица перехода из состояния в состояние определяется графом состояний, который показан на рисунке 1. Вероятности перехода Р, не показаны и определяются из условия полноты вероятностей. 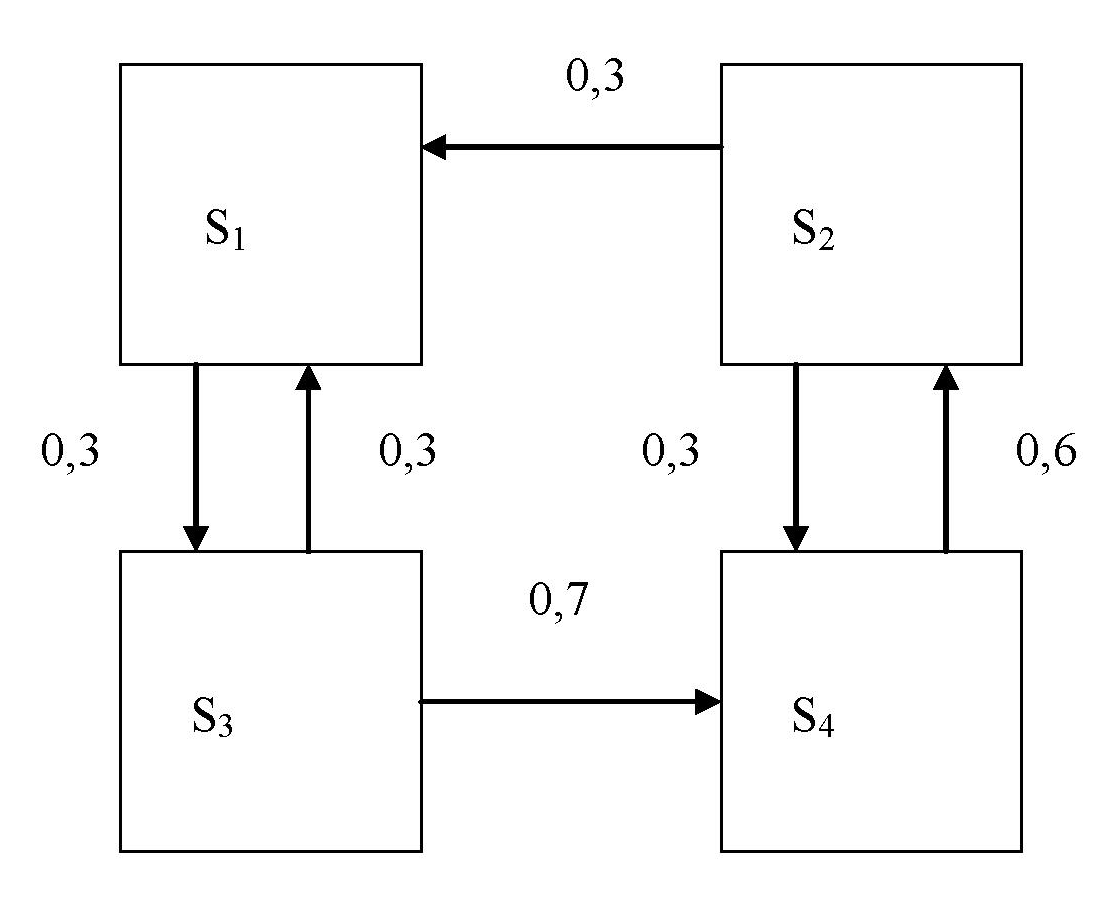 Граф состояний процесса варианта 9 Моделирование процесса Согласно представленному графу состояний, система может находиться в четырех состояниях: S1, S2, S3, S4. В состоянии S1, вектор начального состояния системы в программе принимает значение 1 0 0 0. Поскольку, переходы в то же самое состояние не отображены (согласно условию задания), вероятности переходов можно рассчитать, а затем составить матрицу вероятностей перехода. Матрица вероятностей перехода
 В программе MKV матрица вероятностей перехода будет выглядеть следующим образом: 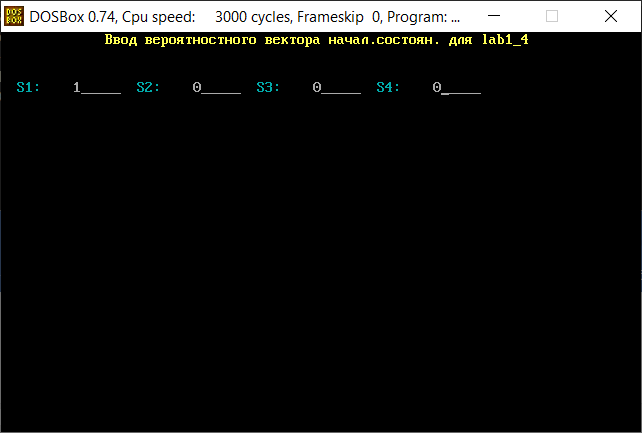 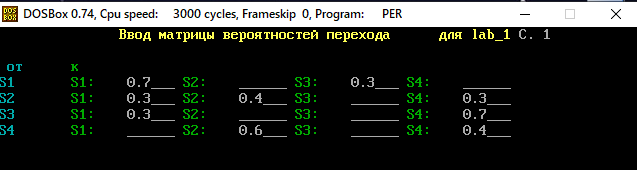 Исходные данные для марковского процесса Вероятность того, что процесс будет находиться в состоянии Si через 2 единицы времени показана на рисунке: 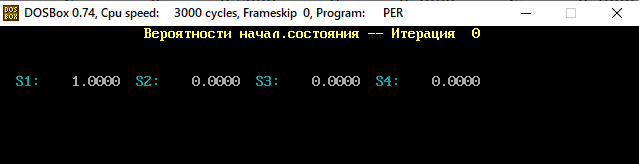 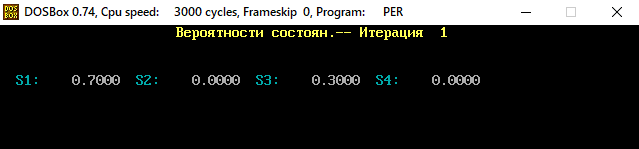 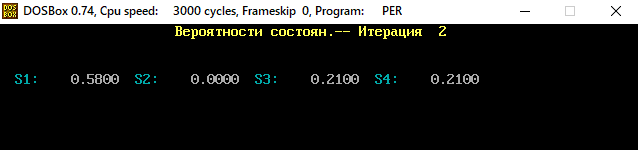 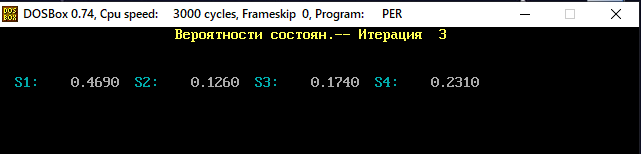 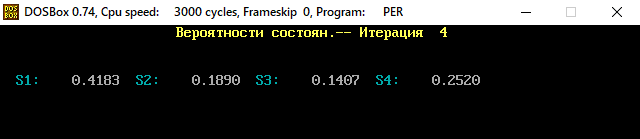 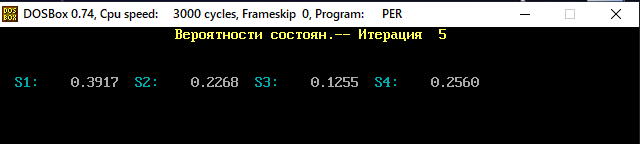 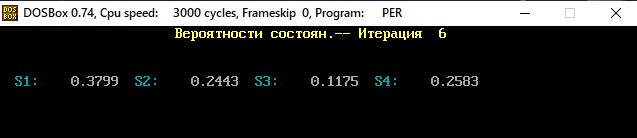 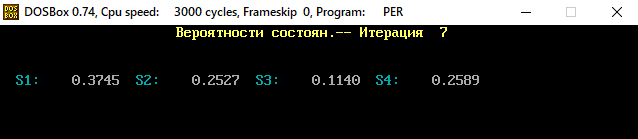 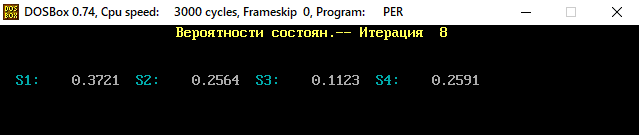 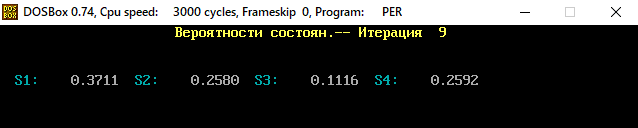 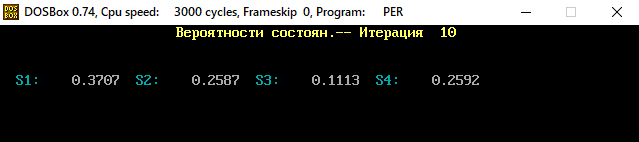 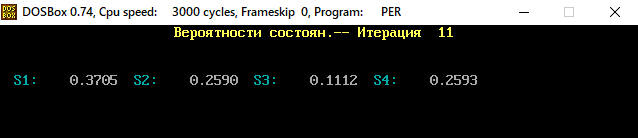 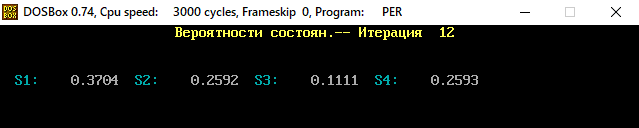 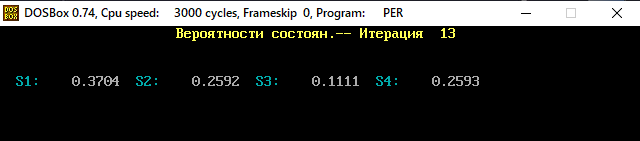 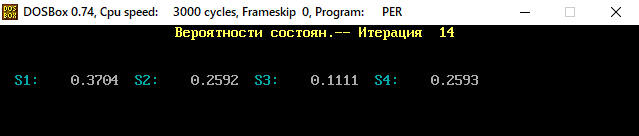 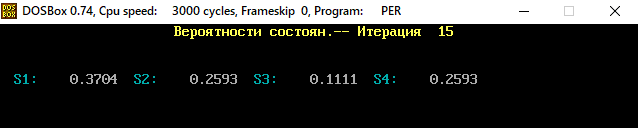 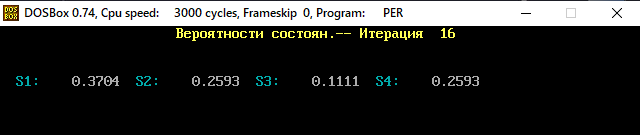 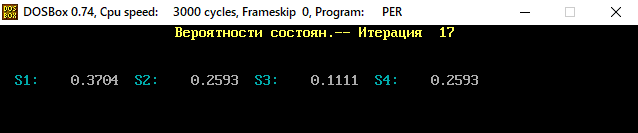 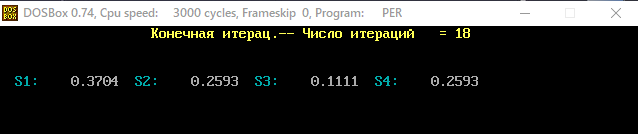 Вероятность состояния Si при итерациях 1-18 Для нахождения устойчивого режима системы применим опцию G. Программа остановится. Результаты решения задачи по поиску значений вероятностей того, что процесс в течение длительного промежутка времени окажется в состоянии S1, S2, S3 и S4 представлены на рисунке. Предельные вероятности для заданного графа определяются за 18 итераций. 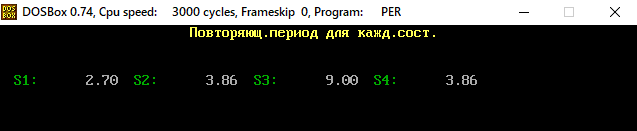 Таблица значений Pi(k)
В результате можно построить графики зависимости вероятностей состояний от числа итераций, представленные на рисунке: 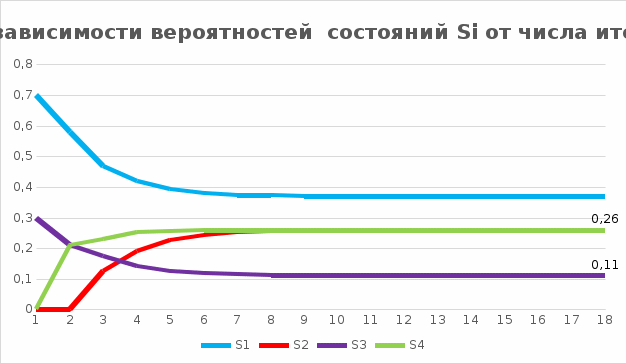 Вывод Представленный процесс является процессом с дискретным временем, поскольку переход из одного состояния в другое возможен только в момент времени k. При помощи программы MKV был смоделирован марковский процесс с дискретными состояниями и дискретным временем и определен период наступления устойчивого режима – 18 итераций. Получены предельные вероятности состояний. Таким образом, в рабочем режиме система будет находиться 37% времени в состоянии S1, 26% времени в состоянии S2, 11% времени в состоянии S3 и 26% времени в состоянии S4. |
