математическое моделирование. Т 1 МАТ. Моделирование. Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205

• Название: Литература по теме 197 Вопрос Узловые операторы. 201 Вопрос Текст программной модели смо. 202 Вопрос Сборка и запуск исполнительного модуля модели. 205
• Анкор: математическое моделирование
• Дата: 02.06.2022
• Размер: 1.51 Mb.
• Имя файла: Т 1 МАТ. Моделирование.docx
• Тип: Литература; #564707
• страница: 4 из 31

Тема 4. Моделирование марковских процессов

Цели изучения темы:

• 
  познакомиться с понятием марковского процесса;
  
• 
  познакомиться с математическим аппаратом моделирования дискретно протекающих марковских процессов.
  

Задачи изучения темы:

• 
  изучить способ математического описания марковских процессов;
  
• 
  научиться определять характеристики марковских процессов с дискретным временем и дискретным множеством состояний.
  

Успешно изучив тему, Вы:

получите представление о:

• 
  сущности марковских процессов и их классификации;
  
• 
  как формулируются задача в терминах марковского процесса;
  
• 
  способах построения математической модели и нахождения с ее помощью значений нужных показателей;
  

будете знать:

• 
  как описать протекающие процессы с помощью графа состояний и переходов;
  
• 
  как найти вектор вероятностей состояния процесса на определенном шаге;
  
• 
  как вычислить предельные вероятности процесса.
  

Вопросы темы:

1. 
   Понятие марковского процесса.
   
2. 
   Классификация марковских процессов.
   
3. 
   Граф состояний и переходов.
   
4. 
   Марковский процесс с дискретными состояниями и дискретным временем.
   
5. 
   Предельные вероятности цепи Маркова.
   

Вопрос 1. Понятие марковского процесса.

Постановка многих задач анализа и, в особенности, проектирования систем связаны с необходимостью проведения оценивания количественных показателей протекающих в системе процессов. Часто поведение этих развивающихся во времени процессов в силу действия различных случайных факторов не удается исследовать во всех деталях. Следствием этого является невозможность в отличие от детерминированных систем однозначно предсказать поведение системы в какой-то момент в будущем. Такие системы и процессы носят название стохастических (от греческого ахо^аанк^ - умеющий угадывать). Их анализ целесообразно проводить, рассматривая их как случайные процессы, ход и исход которых зависят от ряда случайных факторов, сопровождающих их развитие.

Для нахождения числовых значений нужных параметров применяются как аналитические, так и имитационные модели. В настоящей и следующей теме будет рассмотрен подход на основе аналитических моделей. Построение аналитической модели в случае стохастических процессов означает необходимость построения некоторой вероятностной модели явления, в которой будут учтены обусловливающие его развитие случайные факторы.

Для математического описания многих случайных процессов может быть применен аппарат, разработанный в теории вероятностей для так называемых марковских случайных процессов.

Случайный процесс, протекающий в системе S, называется марковским (или процессом без последействия), если он обладает следующим свойством: для каждого момента времени to вероятность любого состояния системы в будущем (при t>to) зависит только от ее состояния в настоящем (при t= to) и не зависит от того, когда и каким

образом система пришла в это состояние (т.е., как развивался процесс в прошлом).

Другими словами, в марковском случайном процессе будущее развитие зависит только от его настоящего состояния и не зависит от «предыстории» процесса.

Вопрос 2. Классификация марковских процессов.

Марковские случайные процессы делятся на классы. Основными классифицирующими признаками являются:

• 
  множество состояний, в которых может находиться система;
  
• 
  моменты времени, в которых происходит изменение состояния системы.
  

Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы Sj, S₂, S₃, ... можно перечислить (перенумеровать) одно за другим, а сам процесс состоит в том, что время от времени система S скачком (мгновенно) переходит из одного состояния в другое.

Кроме процессов с дискретными состояниями существуют случайные процессы с непрерывными состояниями: для этих процессов характерен постепенный, плавный переход из состояния в состояние. Например, процесс изменения напряжения в осветительной сети представляет собой случайный процесс с непрерывными состояниями.

Если переходы системы из состояния в состояние возможны только в определенные моменты времени t_b, t₂, t₃, ... , то марковский процесс относится к процессам с дискретным временем. В противном случае имеет место процесс с непрерывным временем.

Вопрос 3. Граф состояний и переходов.

Анализ случайных процессов с дискретными состояниями обычно проводится с помощью графа состояний и переходов (ГСП).

Пусть имеется система S с n дискретными состояниями:

^SL ^S2^{, S}3 ^, .•• ^{, S}n

Каждое состояние изображается окружностью или прямоугольником (вершина), а возможные переходы из состояния в состояние («перескоки») — стрелками (дугами), соединяющими эти вершины (рис. 8а).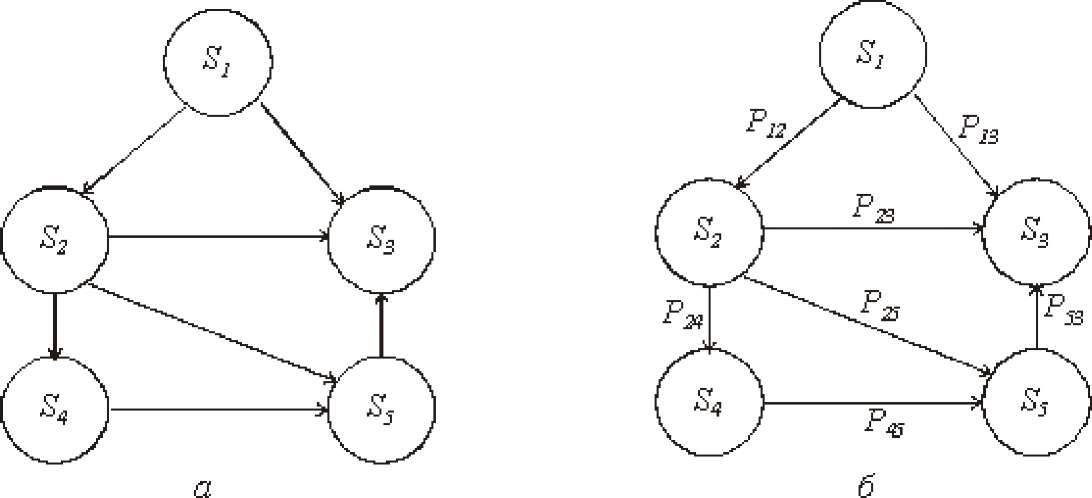




Рис. 8. Пример неразмеченного (а) и размеченного (б) ГСП




Заметим, что стрелками можно отмечать только непосредственные переходы из состояния в состояние; если система может перейти из состояния S_b в S₅ только через S₂, то стрелками отмечаются только переходы S_b—S₂ и S₂—S₅, но не S_b—S₅.

Удобно также пользоваться размеченным графом, который графически изображает не только возможные состояния системы и возможные переходы из состояния в состояние, но также и значения вероятностей перехода (рис. 8 б), о которых речь будет идти ниже.

Вопрос 4. Марковский процесс с дискретными состояниями и дискретным временем.

Пусть система S может находиться в состояниях:

Sj, S2, S3, ... , Sn

и изменения состояния системы возможны только в моменты:

tj, t2, t3, ... , tn

Будем называть эти моменты шагами, или этапами процесса и рассматривать протекающий в системе S случайный процесс как функцию целочисленного аргумента m = J, 2, ... к, ... , обозначающего номер шага.

Указанный случайный процесс состоит в том, что в последовательные моменты времени t_J, t₂, ..., t_k, ... система Sоказывается в тех или иных состояниях. Процесс, происходящий в системе, можно представить как последовательность (цепочку) событий, например:

с(0) о(1) о(0 о(и)

0₁ ^, 0₂ ^, ... ^, S ^, ... ^{, S}_n

называемую марковской цепью, где для каждого шага вероятность перехода из любого состояния Si в любое Sне зависит от того, когда и как система пришла в состояние S_i .

Марковскую цепь можно описать с помощью вероятностей состояний, в которых находится система на каком-то шаге. Пусть в любой момент времени (после любого шага) система может пребывать в одном из состояний:

Sj, S2, S3, . , Sn

т.е., в результате шага к осуществится одно из полной группы несовместных событий:

Ык) Ык) Ык) Ык)

^S₁ ^{, S}₂ ^,...^, s ^,...^{, S}_n . Обозначив вероятности этих событий для k -го шага через р(к) = Ж^(к)), р₂(к) = p(Sf), ... , p (к) = p(S^),..., p, (к) = p(S^) легко видеть, что для каждого шага к

p,(k)+p₂(k)+...+p_t(k)+...+p_n (k)=1

поскольку p (k), i = 1, n , представляют собой вероятности появления полной группы событий.

Вероятности p (k), i = 1, n называются