реферат по математике. реферат матем. Реферат дисциплины Математика По теме Касательная плоскость и нормаль к поверхности. Производная по направлению. Градиент и его свойства.
 Скачать 109.01 Kb. Скачать 109.01 Kb.
|
|
Государственное образовательное учреждение высшего профессионального образования «Ковровская государственная технологическая академия имени В.А. Дегтярева» Кафедра ТМ и САПР РЕФЕРАТ Дисциплины «Математика» По теме «Касательная плоскость и нормаль к поверхности. Производная по направлению. Градиент и его свойства.» Вариант 3. Руководитель: Марихов И. Н. Исполнитель: ст. гр. КТ-120 Афанасьева Н. Н. Ковров 2021 Касательная плоскость и нормаль к поверхности. Касательной плоскостью к поверхности  в точке в точке 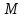 называется плоскость, проходящая через точку называется плоскость, проходящая через точку 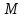 поверхности, если угол между этой плоскостью и секущей, проходящей через точку поверхности, если угол между этой плоскостью и секущей, проходящей через точку 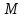 и любую точку и любую точку  поверхности, стремится к нулю, когда точка поверхности, стремится к нулю, когда точка  стремится к точке стремится к точке 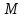 . .Нормалью к поверхности  в точке в точке 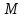 называется прямая, проходящая через точку называется прямая, проходящая через точку 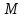 перпендикулярно касательной плоскости в этой точке. перпендикулярно касательной плоскости в этой точке.Если поверхность  задана явно функцией задана явно функцией 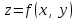 и в точке и в точке  существуют конечные частные производные этой функции, то уравнение касательной плоскости имеет вид: существуют конечные частные производные этой функции, то уравнение касательной плоскости имеет вид: , (1) , (1) а уравнение нормали: 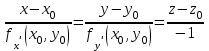 . (2) . (2) Если поверхность  задана неявно уравнением задана неявно уравнением  и в точке и в точке  частные производные функции частные производные функции 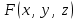 конечны и не обращаются в нуль одновременно, то уравнение касательной плоскости к поверхности в этой точке записывается в виде конечны и не обращаются в нуль одновременно, то уравнение касательной плоскости к поверхности в этой точке записывается в виде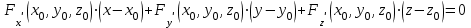 , (3) , (3)а уравнение нормали к поверхности: 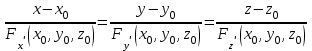 (4) (4)Рассмотрим пример решения задачи Условие. Написать уравнения касательной плоскости и нормали к поверхности 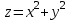 в точке в точке 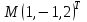 . .Решение. Вычислим частные производные функции 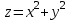 в точке в точке 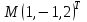 : : , ,  . .Согласно формулам (1) и (2) получим соответственно уравнение касательной плоскости: 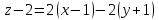 или или 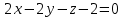 , и уравнение нормали: , и уравнение нормали: 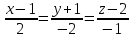 . .Производная по направлению. Производной функции 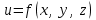 в точке в точке 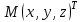 по направлению вектора по направлению вектора 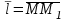 называется предел называется предел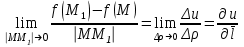 , где , где  . (5) . (5)Если функция 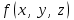 дифференцируема, то производная по направлению вектора дифференцируема, то производная по направлению вектора  находится по формуле находится по формуле , (6) , (6)где 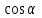 , ,  , , 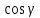 – направляющие косинусы вектора – направляющие косинусы вектора  . . 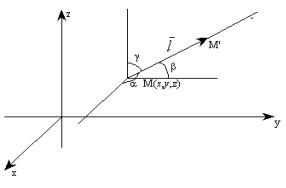 Производная Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке). Как известно, проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению. Градиент и его свойства. Градиентом функции 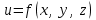 в точке в точке 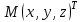 называется вектор с началом в точке называется вектор с началом в точке 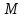 , координатами которого являются значения частных производных функции , координатами которого являются значения частных производных функции  в этой точке: в этой точке: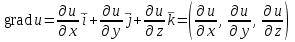 . (5.3) . (5.3)Градиент функции 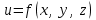 и производная по направлению вектора и производная по направлению вектора  связаны формулой связаны формулой  (5.4), (5.4),где 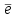 – орт вектора – орт вектора  , который находится по формуле , который находится по формуле  . .Свойства Градиент направлен по нормали к поверхности уровня (или к линии уровня, если поле плоское). Градиент направлен в сторону возрастания функции поля. Модуль градиента равен наибольшей производной по направлению в данной точке поля:  Эти свойства дают инвариантную характеристику градиента. Они говорят о том, что вектор gradU указывает направление и величину наибольшего изменения скалярного поля в данной точке. Замечание. Если функция U(x,y) есть функция двух переменных, то вектор 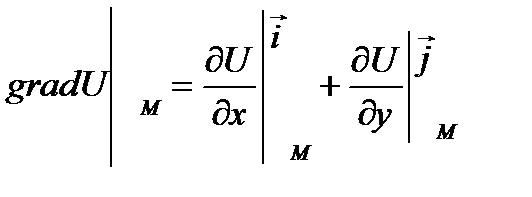 лежит в плоскости oxy. Рассмотрим пример Условие. Дана функция U=x2+y2+z2 . Определить градиент функции в точке М(-2;3;4). Решение. Поверхностями уровня данного скалярного поля являются семейство сфер x2+y2+z2 |
