Криптографияя. Основы криптографии - StudentLib.com. Реферат на тему "Основы криптографии" Томск 2007 содержание введение. Криптография. Основные понятия и определения
 Скачать 0.98 Mb. Скачать 0.98 Mb.
|
|
Министерство образования и науки Российской Федерации (МИНОБРНАУКИ РОССИИ) ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ (ТГУ) Физико-технический факультет РЕФЕРАТ на тему "Основы криптографии" Томск 2007 СОДЕРЖАНИЕ Введение . Криптография. Основные понятия и определения . Методы шифрования . История развития шифров. От первых шифров к современным криптоалгоритмам . Классические шифры . Асимметричная и симметричная криптографии . Хэш-функции и немного об электронной подписи . Электронные водяные знаки . PGP и системы сертификации открытых ключей . Системы идентификации и аутентификации . Ещё немного о криптоанализе Заключение Литература Введение С зарождением человеческой цивилизации возникла необходимость передачи информации одним людям так, чтобы она не становилась известной другим. Сначала люди использовали для передачи сообщений исключительно голос и жесты. С возникновением письменности задача обеспечения секретности и подлинности передаваемых сообщений стала особенно актуальной. Поэтому именно после возникновения письменности появилось искусство тайнописи, искусство "тайно писать" - набор методов, предназначенных для секретной передачи записанных сообщений от одного человека другому. Человечество изобрело большое число способов секретного письма, например, симпатические чернила, которые исчезают вскоре после написания ими текста или невидимы с самого начала, "растворение" нужной информации в сообщении большего размера с совершенно "посторонним" смыслом, подготовка текста при помощи непонятных знаков. Криптография возникла именно как практическая дисциплина, изучающая и разрабатывающая способы шифрования сообщений, то есть при передаче сообщений - не скрывать сам факт передачи, а сделать сообщение недоступным посторонним. Для этого сообщение должно быть записано так, чтобы с его содержимым не мог ознакомиться никто за исключением самих корреспондентов. Появление в середине ХХ столетия первых ЭВМ кардинально изменило ситуацию - практическая криптография сделала в своем развитии огромный скачок и термин "криптография" далеко ушел от своего первоначального значения - "тайнопись", "тайное письмо". Сегодня эта дисциплина объединяет методы защиты информационных взаимодействий совершенно различного характера, опирающиеся на преобразование данных по секретным алгоритмам, включая алгоритмы, использующие секретные параметры. Термин "информационное взаимодействие" или "процесс информационного взаимодействия" здесь обозначает такой процесс взаимодействия двух и более субъектов, основным содержанием которого является передача и/или обработка информации. Базовых методов преобразования информации, которыми располагает современная криптография, немного, но все они являются "кирпичами" для создания прикладных систем. [6] Информация - это одна из самых важных ценностей в современной жизни. Глобальные компьютерные сети упростили доступ к информации как отдельных людей, так и крупных организаций. Однако лёгкость и скорость доступа к данным с помощью таких компьютерных сетей, как Internet, сделали значимыми следующие угрозы безопасности данных при отсутствии мер их защиты: Ø неавторизированный доступ к информации; Ø неавторизированное изменение информации; Ø неавторизированный доступ к сетям и другим сервисам. Криптография представляет собой совокупность методов преобразования (шифрования) данных, направленных на то, чтобы защитить эти данные, сделав их бесполезными для незаконных пользователей. Настоящая криптография (strong cryptography) должна обеспечивать такой уровень секретности, чтобы можно было надежно защитить критическую информацию от расшифровки крупными организациями - такими как мафия, транснациональные корпорации и крупные государства. [3] На сегодняшний день криптографические методы применяются для идентификации и аутентификации пользователей, защиты каналов передачи данных от навязывания ложных данных, защиты электронных документов от копирования и подделки. Данный реферат посвящен этой теме. Цель данной работы состоит в получении знаний о криптографии, в знакомстве с современными методами шифрования и применении полученной информации в своей дальнейшей практической деятельности. Задачи: 1. Рассмотреть историю развития криптографии. 2. Познакомиться с современными методами шифрования. . Узнать особенности математического представления криптографии. Криптография - важный элемент защиты данных, она позволяет успешно решить ряд проблем информационной безопасности компьютерных систем и сетей. Естественно, меня заинтересовала криптографическая защита информации, так как это очень актуальный вопрос в современной жизни. Что обычно приходит на ум при произнесении слова "криптография"? Спецслужбы, дипломатическая переписка, "математическое шаманство"? А при произнесении фразы "криптография в информационных технологиях"? Шифрование данных припомнят сразу. Про электронную подпись вспомнят. Кто-то знает что-то про "Сертификаты открытых ключей". Или про "взлом" чужих шифров. Попробуем разобраться со всеми этими, а заодно и другими, понятиями и подходами, которыми оперирует современная криптография. 1. Криптография. Основные понятия и определения Криптография в прошлом использовалась лишь в военных целях. Однако сейчас, по мере образования информационного общества, криптография становится одним из основных инструментов, обеспечивающих конфиденциальность, доверие, авторизацию, электронные платежи, корпоративную безопасность и бесчисленное множество других важных вещей. Но криптография - не панацея от всех бед. Криптографические методы могут помочь обеспечить безопасность, но только на эти методы надеяться не следует. Криптография позволяет реализовывать следующие механизмы защиты информации: Ø шифрование данных, передаваемых по каналам связи или хранимым в базах данных; Ø контроль целостности данных, передаваемых по каналам связи; Ø идентификация (опознавание) субъекта или объекта системы (сети); Ø аутентификация (проверка подлинности) субъекта или объекта сети; Ø контроль (разграничение) доступа к ресурсам системы (сети). Базовых методов преобразования информации, которыми располагает криптография, немного, среди них: Ø шифрование (симметричное и несимметричное); Ø вычисление хэш-функций; Ø генерация электронной цифровой подписи; Ø генерация последовательности псевдослучайных чисел. [3] . Методы шифрования В данной работе нас будут интересовать криптосистемы и криптоалгоритмы, реализованные с использованием компьютера. В реферате не будут рассмотрены методы шифрования с использованием шифроблокнотов или специальной шифровальной техники как в силу недостатка открытой информации об этих методах, так и в силу недоступности такого оборудования массовому потребителю. Основой большинства механизмов защиты информации является шифрование данных. Шифрование - это преобразование данных в нечитабельную форму при помощи ключей шифрования. Методов шифрования было придумано множество - от шифров простой замены (наиболее известный пример - "Пляшущие человечки" Конан Дойля) до принципиально невскрываемого шифра Вернама (двоичное сложение исходного текста с однократно используемой случайной последовательностью). Обобщённая схема криптосистемы, обеспечивающей шифрование передаваемой информации, показана на рисунке: 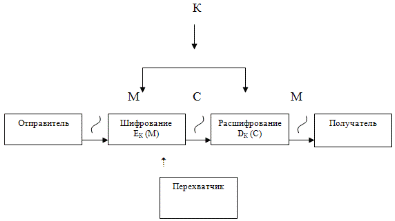 Отправитель генерирует открытый текст исходного сообщения M, которое должно быть передано законному получателю по незащищённому каналу. За каналом следит злоумышленник с целью перехватить и раскрыть передаваемое сообщение. Для того чтобы перехватчик не смог узнать содержание сообщения M, отправитель шифрует его с помощью обратимого преобразования ЕК и получает шифртекст (или криптограмму) C = ЕК (М), который отправляет получателю. Законный получатель, приняв шифртекст C, расшифровывает его с помощью обратного преобразования D = ЕК-1 и получает исходное сообщение в виде открытого текста M: DК (C) = ЕК-1 (ЕК (М)) = M. Преобразование выбирается из семейства криптографических преобразований, называемых криптоалгоритмами. Параметр, с помощью которого выбирается отдельное используемое преобразование, называется криптографическим ключом К. Ключ К может принадлежать конкретному пользователю или группе пользователей и являться для них уникальным; зашифрованная с использованием конкретного ключа информация может быть расшифрована только его владельцем (владельцами). Где-то даже довелось прочесть такое определение шифрованию: "Шифрование - это процесс замены Вашего большого секрета (документа) маленьким (ключом)". Криптосистема имеет разные варианты реализации: набор инструкций, аппаратные средства, комплекс программ компьютера, которые позволяют зашифровать открытый текст и расшифровать шифртекст различными способами, один из которых и выбирается с помощью конкретного ключа К. Говоря более формально, криптографическая система - это однопараметрическое семейство (ЕК) 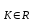 обратимых преобразований ЕК : обратимых преобразований ЕК : 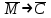 из пространства из пространства 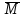 сообщений открытого текста в пространство сообщений открытого текста в пространство  шифрованных текстов. Параметр К (ключ) выбирается из конечного множества шифрованных текстов. Параметр К (ключ) выбирается из конечного множества  , называемого пространством ключей. , называемого пространством ключей.Вообще говоря, преобразование шифрования может быть симметричным или асимметричным относительно преобразования расшифрования. Это важное свойство функции преобразования определяет два класса криптосистем: Ø симметричные криптосистемы (с одним ключом); Ø асимметричные криптосистемы (с двумя ключами). В симметричной криптосистеме используются одинаковые ключи в блоке шифрования и блоке расшифрования. Это означает, что любой, кто имеет доступ к ключу шифрования, может расшифровать сообщение. Именно поэтому симметричные криптосистемы называют криптосистемами с секретным ключом - ключ шифрования должен быть доступен только тем, кому предназначено сообщение. Задача обеспечения конфиденциальности передачи электронных документов с помощью симметричной криптосистемы сводится к обеспечению конфиденциальности ключа шифрования. Симметричное шифрование неудобно тем, что перед началом обмена зашифрованными данными необходимо обменяться секретными ключами со всеми адресатами. Передача секретного ключа симметричной криптосистемы не может быть осуществлена по общедоступным каналам связи; секретный ключ надо передавать отправителю и получателю по защищённому каналу распространения ключей. Симметричное шифрование идеально подходит на случай шифрования информации "для себя", например с целью предотвратить несанкционированный доступ к ней в отсутствие владельца. Это может быть как архивное шифрование выбранных файлов, так и прозрачное (автоматическое) шифрование целых логических или физических дисков. Принципиальное отличие асимметричной криптосистемы от симметричной состоит в том, что для зашифрования информации и её последующего расшифрования используются различные ключи: Ø открытый ключ К1 используется для зашифрования информации. Вычисляется из секретного ключа К2; Ø секретный ключ К2 используется для расшифрования информации, зашифрованной с помощью парного ему открытого ключа К1. Секретный и открытый ключи генерируются попарно. Секретный ключ К2 остаётся у его владельца; он должен быть надёжно защищён от несанкционированного доступа (аналогично ключу шифрования в симметричных криптосистемах). Копия открытого ключа К1 должна находиться у каждого абонента сети, с которым обменивается информацией владелец секретного ключа, то есть в асимметричной криптосистеме передают по незащищённому каналу только открытый ключ, а секретный обычно сохраняют на месте его генерации. Любая попытка со стороны перехватчика расшифровать текст C для получения открытого текста M или зашифровать собственный текст M' для получения правдоподобного шифртекста C’, не имея подлинного ключа, называется криптоаналитической атакой. Криптоанализ - это наука о раскрытии исходного текста зашифрованного сообщения без доступа к ключу. Успешный анализ может раскрыть исходный текст или ключ. Он позволяет также обнаружить слабые места в криптосистеме, что в конечном счёте ведёт к тем же результатам. [2] Фундаментальное правило криптоанализа, впервые сформулированное голландцем А. Керкхоффом ещё в XIX веке, заключается в том, что стойкость шифра (криптосистемы) должна определяться только секретностью ключа. Иными словами, правило Крекхоффа указывает на то, что весь алгоритм шифрования, кроме значения секретного ключа, известен криптоаналитику противника. Это обусловлено тем, что криптосистема, реализующая семейство криптографических преобразований, обычно рассматривается как открытая система. Такой подход отражает очень важный принцип технологии защиты информации: защищённость системы не должна зависеть от секретности чего-либо такого, что невозможно быстро изменить в случае утечки секретной информации. Обычно криптосистема представляет собой совокупность аппаратных и программных средств, которую можно изменить только при значительных затратах времени и финансов, тогда как ключ является легко изменяемым объектом. Именно поэтому стойкость криптосистемы определяется только секретностью ключа. [5] 3. История развития шифров. От первых шифров к современным криптоалгоритмам Существуют два основных вида шифров: шифр перестановки и шифр замены. Шифр перестановки осуществляет преобразование перестановки символов в открытом тексте. Шифр замены осуществляет преобразование замены символов открытого текста на другие символы зашифрованного текста. Шифры перестановки и замены имеют долгую историю развития и использования. Известно, что в V веке до нашей эры правители Спарты - наиболее воинственного из греческих государств - имели хорошо отработанную систему секретной военной связи и шифровали свои послания с помощью "Скитала", первого простейшего криптографического устройства, реализующего метод простой перестановки. Шифрование выполнялось следующим образом. На жезл, имеющий форму цилиндра, наматывалась по спирали узкая папирусная лента (без просветов и нахлестов), а затем на этой ленте вдоль оси цилиндра писали несколько строк текста сообщения. Затем лента разматывалась. Для непосвящённых получалось, что поперёк ленты в беспорядке написаны какие-то буквы. Адресат брал такой же жезл и таким же образом наматывал на него полученную ленту, восстанавливая тем самым исходное сообщение. По названию жезла и получил название этот шифр. Другим примером шифра древности является шифр Цезаря. Этот шифр простой замены реализует следующие преобразования текста: каждая буква открытого текста заменялась третьей после неё буквой в латинском алфавите, который считался написанный по кругу, то есть после буквы Z следует буква A (в русском алфавите соответственно после буквы Я следует буква А). Более широкий круг пользователей имел шифр российского посольского приказа, называвшийся "Тарабарской грамотой". Суть этого шифра сводилась к тому, что алфавит делился на две части, и в зашифрованном тексте первая буква первой части алфавита заменялась на первую букву второй части алфавита и наоборот. Следует отметить, что до 1708 года использовавшийся русский алфавит - кириллица - состоял из 42 букв. Вплоть до начала XX века, когда появились первые шифровальные машины, криптография была уделом любителей-одиночек. Понимание математического характера решаемых криптографией задач пришло только в середине XX века после выхода в свет работ американского учёного Клода Шеннона. В 1945 году вышла его работа "Математическая теория криптографии", которая была рассекречена в 1948 году. На основе анализа существовавших шифров К. Шеннон сделал вывод, что во всех, даже очень сложных шифрах в качестве типовых компонентов можно выделить простые приемы, которые представляют собой шифры замены и перестановки. Математическое описание шифра замены выглядит следующим образом. Пусть X и Y - два алфавита (открытый и шифрованный соответственно). Обозначим через g: X  Y взаимно однозначное отображение алфавитов X и Y. Y взаимно однозначное отображение алфавитов X и Y.Действие шифра замены можно представить как преобразование открытого текста (x1, x2, … xn) в шифрованный (y1, y2, … yn), причём y1 = g (x1), y2 = g (x2), … yn = g (xn). Математическое описание шифра перестановки выглядит следующим образом. Пусть длина отрезков, на которые разбивается открытый текст, равна n, а σ - взаимно однозначное отображение множества {1, 2, … n} в себя. Шифр перестановки действует так: отрезок открытого текста x1, x2, … xn преобразуется в отрезок шифрованного текста xσ (1), xσ (2), … xσ (n) . Очень важным для развития криптографии явился вывод К. Шеннона о существовании и единственности абсолютно стойкого шифра. Таким единственным шифром является одноразовая (однократная) система шифрования, в которой открытый текст объединяется с полностью случайным ключом такой же длины. На практике абсолютно стойкие шифры применяются в сетях связи с небольшим объёмом передаваемой информации, которые используют для передачи сообщений особой государственной важности. Это обусловлено тем, что каждый передаваемый текст должен иметь свой собственный, абсолютно случайный, единственный и неповторяемый ключ. Следовательно, перед использованием этого шифра все абоненты должны быть обеспечены остаточным количеством случайных ключей, и при этом исключена возможность их постоянного использования. Выполнение этих требований - очень трудная и дорогая задача. Классический симметричный шифр, описанный К. Шенноном, можно представить следующим образом. Для этого шифра определены две функции - функция шифрования и функция расшифрования. Функция шифрования осуществляет преобразование открытого текста в зашифрованный (например, F: X  Y). Y).Функция расшифрования выполняет обратную процедуру (например, F-1: Y  X). [2] X). [2]. Классические шифры Вообще "классическими шифрами" принято называть симметричные блочные шифры. То есть те, которые для шифрования и расшифрования информации используют один и тот же ключ и шифруют информацию блоками. Длина блока обычно составляет 8 или 16 байт. Есть алгоритмы, допускающие переменную длину блока. Первым блочным шифром, широко использующимся на практике, стал DES (Data Encryption Standard), разработанный специалистами IBM в начале 70х годов прошлого века и долгое время служивший стандартом для шифрования данных в США. Потом появилось много блочных алгоритмов - IDEA, Blowfish, советский ГОСТ28147 89 (и ныне являющийся отечественным стандартом). Оригинальный DES, к примеру, использовал ключ длиной 112 бит и блок шифрования длиной 64 бита. Но после его "анализа" специалистами NSA1 длина ключа была уменьшена до 64 бит. При этом в ключе было только 56 бит уникальных, а 8 бит - контрольных, служащих для контроля целостности ключа. Именно с ключом длиной в 56 бит DES и был утвержден в качестве Национального Стандарта. При том уровне развития вычислительной техники задача перебора 2**56 ключей за приемлемое время была или технически не выполнимой, или неоправданно дорогой. Сейчас DES с длиной ключа в 56 бит не представляется стойким алгоритмом. Большинство современных стойких симметричных алгоритмов используют ключ длиной 64-256 бит (8-32 байта). Необходимо отметить, что кроме блочных шифров существуют и активно используются поточные шифры. Они, как и блочные шифры, используют симметричный ключ, но выполняют шифрование входного потока побайтно или иногда побитно. Идея поточного шифра состоит в том, что на основе симметричного ключа вырабатывается ключевая последовательность или гамма-последовательность, которая складывается по модулю два (операция xor) с входным потоком. Поточные шифры, как правило, более производительны, чем блочные, и используются для шифрования речи, сетевого трафика и иных данных с заранее неизвестной длиной. При достаточно частой смене ключа для выработки гаммы поточные шифры обеспечивают достаточную стойкость. Вектор инициализации, как видно из его названия, является инициализирующей двоичной посылкой длиной равной блоку алгоритма. Вектор инициализации не является секретным элементом. В частности, в мобильной связи стандартом GSM предусмотрена возможность шифрования передаваемого голосового потока на участке от телефонного аппарата до базовой станции шифром A5, который является поточным. С алгоритмом A5 связана одна поучительная история. Изначально описание алгоритма A5 было закрытым. Но из-за юридической ошибки компании владельца алгоритма его описание попало в Интернет, и алгоритм был проанализирован. Его стойкость оказалась даже ниже стойкости DES. Осознав важность открытости алгоритмов для обеспечения их стойкости, разработчики третьего поколения сети GSM пообещали сделать предлагаемые к использованию алгоритмы шифрования голоса достоянием широкой криптографической общественности. Пример показывает важность наличия открытого описания алгоритма даже для самих его разработчиков. На сегодняшний день алгоритмы с длиной ключа 64 и больше бит обеспечивают приемлемую стойкость. Однако зачем тогда использовать ключи длиной 512 и более бит? Ответ таков- эти ключи от другого замка! В 1976 году была опубликована работа американских математиков У. Диффи и М. Хеллмана "Новые направления в криптографии". В этой работе была предложена и обоснована методология асимметричного шифрования, которая базируется на применении однонаправленных функций. Диффи и Хеллман придумали абсолютно "новую" криптографию - криптографию с открытым ключом. Еще ее называют "открытой криптографией" или "асимметричной криптографией". [6] . Асимметричная и симметричная криптографии Идея Диффи и Хеллмана состояла в следующем. Возьмём некоторое число и назовем его "секретным ключом". Произведём над ним некоторые действия, в результате которых получим другое число - "открытый ключ". Причем выберем такие действия, что получить "открытый ключ" по известному "секретному" не будет требовать больших вычислительных ресурсов и времени, а обратное действие - вычисление по "открытому ключу" "секретного" - окажется невозможным или очень длительным. Не вдаваясь в математические подробности, отметим, что на современном персональном компьютере генерация открытого ключа по известному секретному ключу производится за время порядка секунды, а на обратное преобразование, в зависимости от длины ключа, может уйти до сотен (и даже тысяч) лет. Рассматривая исходный текст как некоторое большое число, произведем его преобразование с использованием открытого ключа. В результате получим новое число, которое будем рассматривать как шифр. Имея в распоряжении секретный ключ и используя тот факт, что открытый ключ был получен из секретного специальным образом, мы можем относительно быстро (в вычислительном плане) расшифровать текст. При этом надо заметить, что в целом процесс шифрования/расшифрования с использованием пары ключей проходит на два-три порядка медленнее, чем шифрование/расшифрование того же текста симметричным алгоритмом. [4] Казалось бы, зачем нужно использовать относительно медленную асимметричную криптографию при наличии быстрых и проверенных временем и практикой симметричных алгоритмов? Нужно это за тем, что при использовании асимметричной криптографии радикально упрощается процедура распределения ключей между участниками обмена, а также становится возможным использование электронно-цифровой подписи. Самым известным асимметричным алгоритмом шифрования на сегодняшний день является алгоритм, предложенный Ривестом, Шамиром и Адельманом и носящий их имена, - алгоритм RSA. В самом деле, если участников обмена немного, и все они находятся недалеко друг от друга, то проблема распределения между ними симметричных ключей решается относительно просто. Для связи "каждый с каждым" N участникам обмена каждому из них необходимо иметь N1 ключей парной связи. При этом каждый участник обмена должен иметь безопасный канал обмена ключами с остальными участниками. При увеличении числа участников обмена задача распределения и замены скомпрометированных симметричных ключей может оказаться и вовсе неразрешимой, особенно тогда, когда участники обмена не доверяют друг другу. Использование асимметричной криптографии радикально упрощает процесс распределения ключей. Открытый ключ потому и назвали "открытым", что он не представляет секрета. Можно создать общедоступный "справочник открытых ключей", куда можно поместить открытые ключи всех участников обмена. При этом каждый владелец ключа волен отозвать свой ключ из справочника или заменить его - эта процедура не отразится на остальных участниках обмена. При этом возникает проблема подлинности ключа в справочнике, но и она разрешима. Но за удобство надо платить. В случае использования асимметричной криптографии платой является время и длины ключей. При использовании асимметричной криптографии характерной длиной ключей является 512-1024 бит. Сейчас, когда стали доступны высокопроизводительные вычислительные системы, набирает популярность использование 2048-битных ключей. Можно ли сократить время шифрования, сохранив удобство асимметричной криптографии и добавив скорость блочных шифров? Оказывается, можно. Обычно поступают так: вырабатывают случайную (или псевдослучайную) последовательность и используют ее в качестве одноразового (так называемого сеансового) ключа для шифрования документа быстрым симметричным алгоритмом. Затем, используя асимметричный алгоритм, шифруют сеансовый ключ и передают его в зашифрованном виде вместе с документом. При расшифровании документа сначала расшифровывают сеансовый ключ, а затем и сам документ. Из-за того, что сеансовый ключ имеет малую длину, на его шифрование тратится немного времени. Используемые сейчас симметричные криптоалгоритмы имеют производительность порядка мегабайта в секунду (для программных реализаций) и десятков мегабайт в случае использования специализированных криптопроцессоров. Асимметричные алгоритмы показывают производительность от единиц до десятков килобайт в секунду, в зависимости от длины ключа. При длине сеансового ключа в 8-32 байта подобная гибридная криптосхема оказывается вполне эффективной. Но вернемся ненадолго к оценкам стойкости асимметричных алгоритмов и к проблемам, возникающим при их использовании. В настоящем обзоре мы постараемся обойтись без математических выкладок и формул, однако, отметим, что сложность восстановления секретного ключа по открытому определяется сложностью разложения большого числа на простые сомножители (так называемая "задача факторизации") или сложностью задачи "дискретного логарифмирования". Задачу "дискретного логарифмирования" можно сформулировать так: взяли некоторое известное число, возвели его в неизвестную степень и остаток от деления этой экспоненты на некоторое известное большое простое число (так называемый модуль) сообщили в качестве результата. Все числа натуральные. Нужно найти показатель степени. Характерные длины чисел, участвующих в вычислениях, - несколько сотен десятичных разрядов (вот те самые 512-1024-2048 бит). Сегодняшние результаты теории сложности гласят, что вычислительная сложность задачи дискретного логарифмирования экспоненциально зависит от величины модуля. Но никому ещё не удалось строго доказать, что эта зависимость не может быть полиномиальной. Если вдруг завтра какой нибудь гениальный математик найдет быстрый способ факторизации больших чисел, то может случиться так, что мы окажемся без асимметричной криптографии. Хотя вероятность этого события математики оценивают как близкую к нулевой. Используя асимметричную криптографию, полезно помнить об этаком "дамокловом мече". [6] |
